Descrição
Dimensionamento de estacas com momento fletor e força cortante
Uma das maiores dúvidas de engenheiros recém formados é:
Como considerar momentos fletores e forças cortantes no cálculo de blocos e no dimensionamento de estacas?
O fato é que na universidade raramente esses conceitos são abordados na prática, e na minha opinião, essa é mais uma das lacunas e desafios que o engenheiro projetista encontrará em seu percurso, eu vou lhe explicar porque.
Didaticamente, bloco sujeito a compressão simples é mais fácil
Uma das minhas primeiras observações é essa.
Compressão simples facilita muito a vida e o entendimento do deslocamento das cargas nas fundações de blocos sobre estacas.
Porém, assumir essa hipótese de carregamento é privilégio para as fundações de maneira geral.
A predominância de esforços de compressão ocorre frequentemente em pilares centrais travados, que são apenas um dos tipos de pilares que existe.
Assim, essa hipótese não se aplica por exemplo em pilares de canto, pilares de extremidade. E é aí então que começam as dúvidas.
Modelos de Cálculo para o Dimensionamento de Estacas São Complexos
Existem alguns modelos matemáticos simplificados que tentam explicar o comportamento dos esforços e a interação bloco-estaca-solo.
Alguns desses modelos, datam do século XIX, o que mostra, ao meu ver, por um lado a incapacidade intelectual do estado da arte em desenvolver boas aproximações analíticas para condições de carregamento e esforços complexas.
Em outras palavras, uma linha óbvia para esta área da engenharia é a utilização de elementos finitos discretizados para o entendimento do comportamento da estrutura nesses casos e isso, à nível científico, é o que há de melhor.
Porém, mais uma vez, quando falamos de praticidade é aí que a coisa complica.
Precisamos ainda de soluções mais rápidas e factíveis para lançarmos nossas obras e executa-las.
Eis então a justificativa de se voltar a época onde não haviam computadores, calculadoras, mas, sobretudo, excelente capacidade de analogia.
Assim, nessa planilha utilizamos métodos simplificados, mas comprovadamente testados.
Portanto, desenvolvemos essa planilha para resolver o seguinte problema:
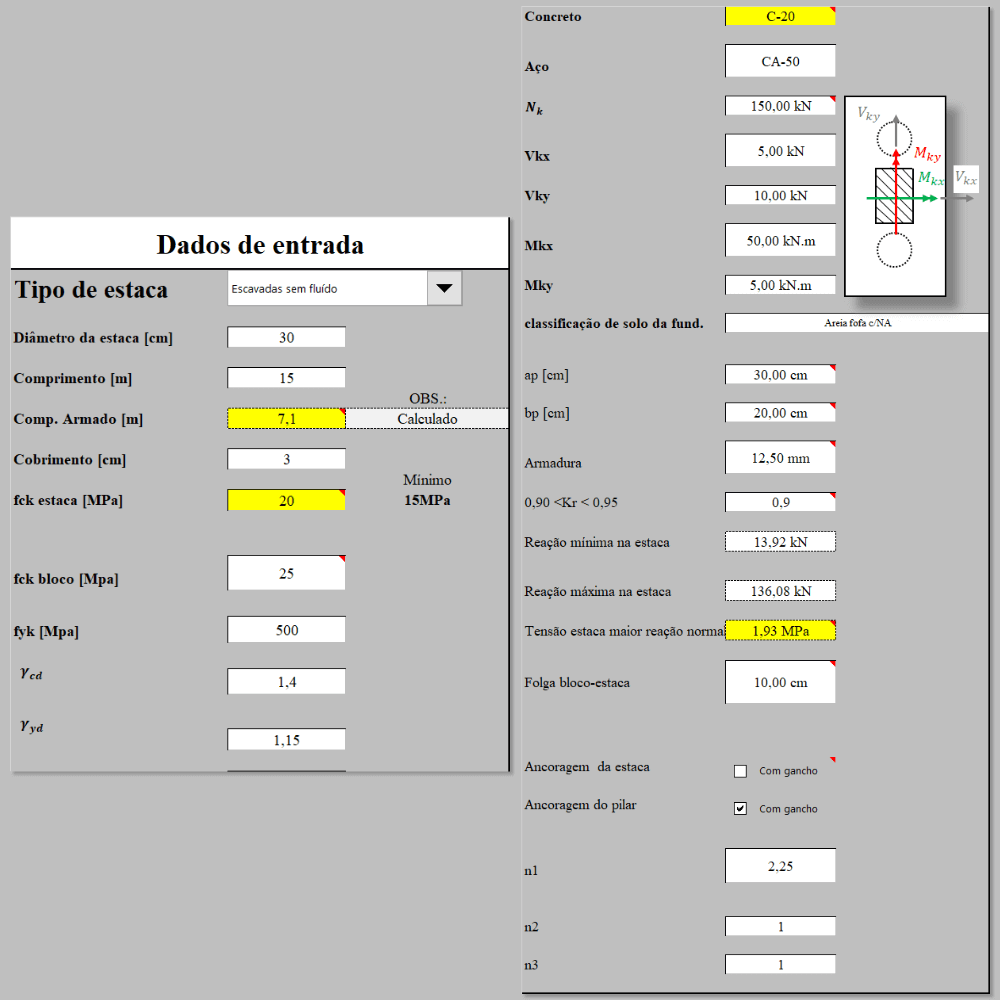
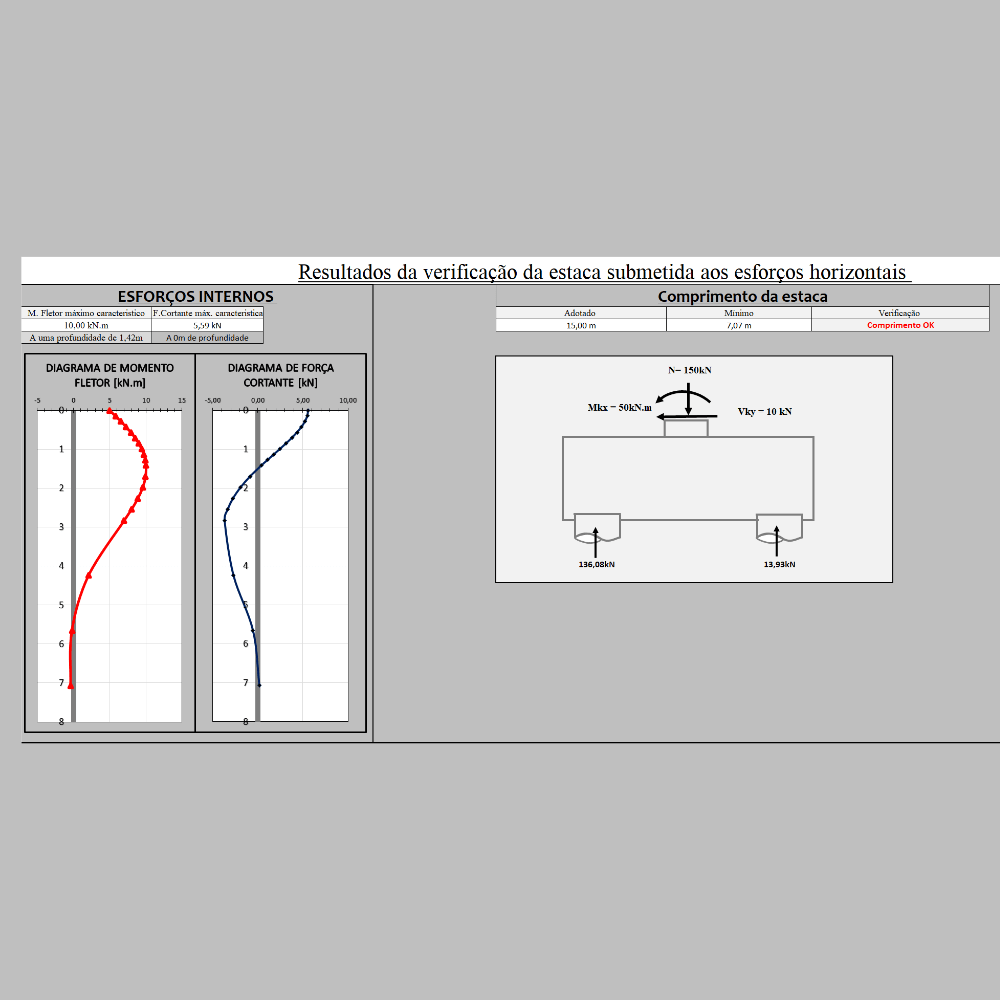
a) Estimar com propriedade os diagramas de:
i) Momento fletor nas duas direções principais
ii) Forças cortante nas duas direções principais
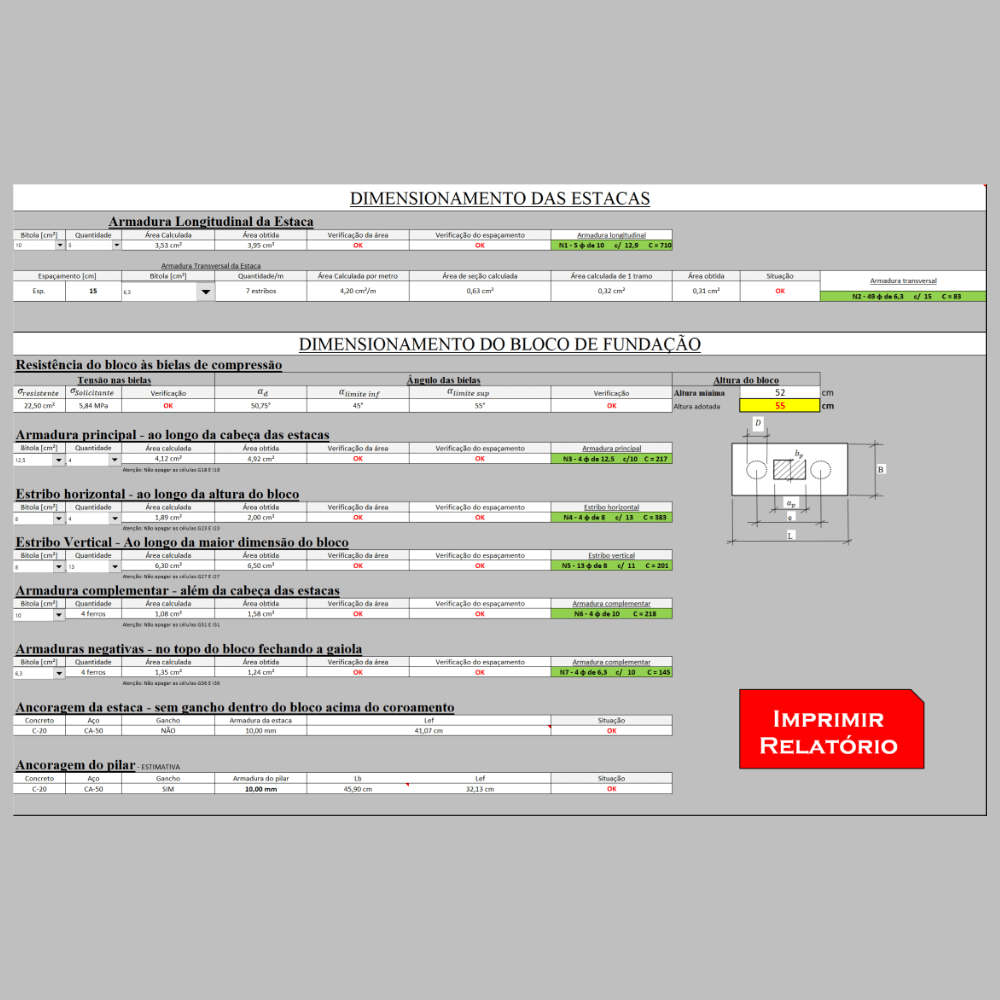
b) Dimensionar as seções críticas
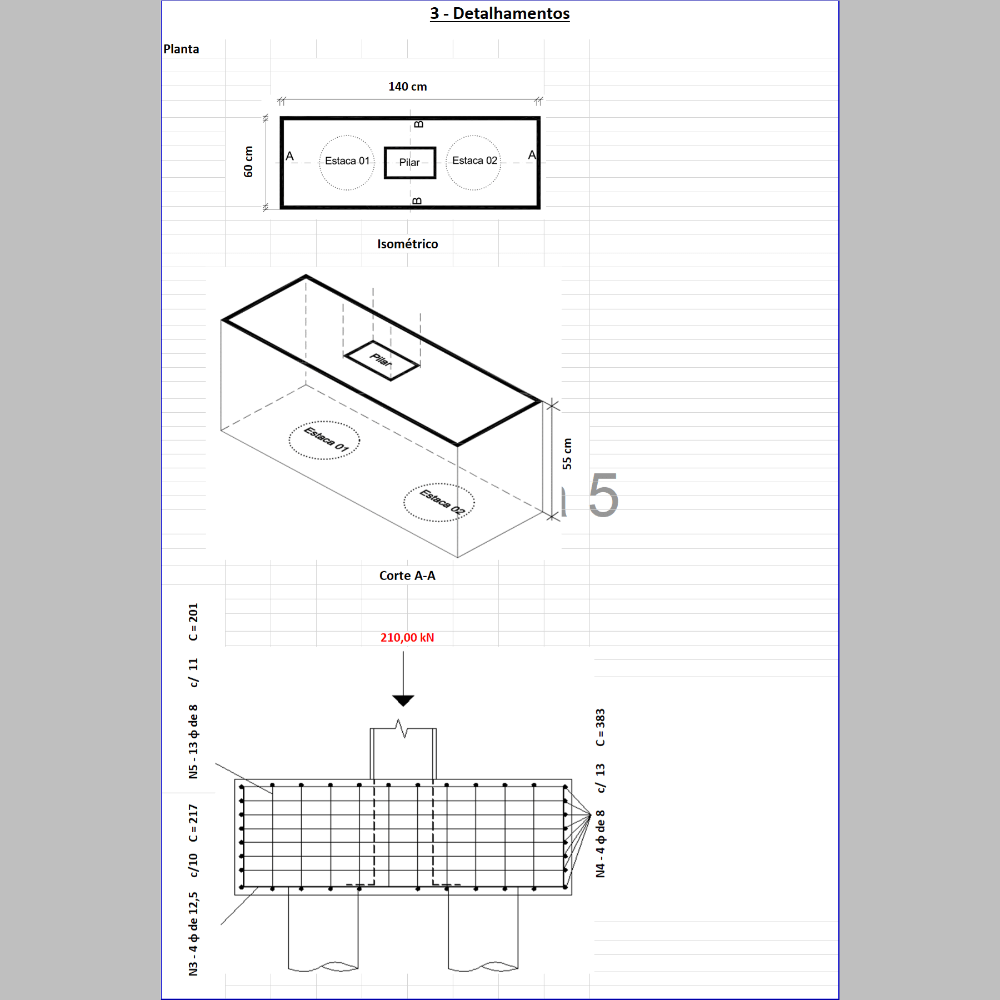
c) Detalhar as armaduras
d) Fornecer memorial de cálculo tanto para o bloco quanto para a estaca
Desse modo, a planilha de dimensionamento de estacas e blocos com momentos fletores e força cortante é uma das mais inovadoras e promete lhe trazer muita segurança, agilidade e praticidade.
Um dos Maiores Erros no Projeto de Blocos de Duas Estacas
Quando estamos falando de casos onde forças horizontais e momentos fletores são desprezíveis no topo do bloco, o cálculo das estacas é praticamente à compressão.
Porém, quando há momentos e principalmente forças horizontais, as estacas passam a ser submetidas a esforços que podem gerar diagramas de força cortante e de momento fletor ao longo do comprimento da estaca.
O que muitos por ai têm feito e que é um erro é considerar o seguinte. Imagine que há um momento fletor na cabeça do bloco $M_r$.
Esse momento $M_r$ pode ser descrito por um binário de forças, de modo que:
$$ M_r = F_d \times e$$
onde $F_d$ é o binário de forças (compressão em uma estaca e tração na outra) e $e$ é a distância de centro a centro da estaca.
Assim, o esforço único e exclusivo na estaca seria apenas a força $F_d$ e, assim, o cálculo da armadura da estaca tracionada seria
$$ A_s = \frac{F_d}{f_{yd}}$$
onde $f_{yd}$ é a resistência de projeto do aço e $A_s$ a área de armadura de tração.
Porém se pergunte: quem gerou esse momento $M_r$ na cabeça da estaca? Foi por acaso o esforço horizontal de empuxo na lateral de um muro?
O Esforço Lateral Não Some do Dimensionamento de Estacas!
Parece bobagem, mas muitos engenheiros simplesmente fazem mágica nesse momento. Eles simplesmente assumem uma flexão simples e esquecem da razão que gerou o momento, ou seja, a força horizontal $E$ multiplicada pelo braço de alavanca do muro $h/3$.
Essa força horizontal atua na cabeça do bloco e, se o bloco tem uma altura $h_b$, o novo momento que de fato atua na cabeça da estaca é:
$$M_r^* = M_r + E \times h_b$$
Assim, há um tremendo esforço horizontal na cabeça da estaca mais um momento no topo.
Se assumirmos uma simplificação que essa combinação de esforços se divide igualmente para as duas estacas, ai sim temos condiçao de calcular o diagrama de momentos fletores e forças cortantes.
Não se dá para sumir com o esforço horizontal!!!
Caso queira saber mais sobre o método de dimensionamento das estacas, confira a teoria do método de Matlock e Reese, que, resumidamente, assume um comportamento elástico na estaca e considera as reações do solo no perímetro da estaca.
Quer fazer projetos seguros?
Se o valor da planilha for demais para você, paciência. Esse é um produto personalizável, dentro das normas e totalmente diferente do que se tem ai na internet.
Mas só lhe peço uma coisa: não suma com o esforço horizontal no seu projeto! Newton agradece.
Adquira já nossa planilha para ter uma ferramenta completa para o projeto de bloco de duas estacas para qualquer condição de carregamento.








Avaliações
Não há avaliações ainda.