Onde $f_a$ é um fator de conversão de custos em valor presente para um valor anual equivalente, $n$ é a vida útil do projeto e $P$ são valores anuais que ocorrem ao longo da vida útil (e.g., custo com energia).

Os outros custos de implantação estão em valores presente; assim, basta considerarmos todos os custos em uma única base de tempo

Nesse texto usamos a base anual, ou seja, todos os custos serão balizados para valores anuais equivalentes.

Portanto, para decidir o sistema com o diâmetro econômico, simplesmente escolhemos aquele com menor valor anual equivalente.

Nos próximos itens vamos detalhar como chegar nesses custos.

Cálculos Hidráulicos Preliminares

O primeiro cálculo é o da perda de carga total entre a bomba e o reservatório superior.

Para isso, resolvemos a equação de Darcy-Weisbach entre esses dois pontos.

Essa perda de carga deve levar em conta a perda de carga distribuída e localizada desse trecho.

Assim, podemos estimar a altura manométrica de um sistema que tem um comprimento $L$, e diâmetro $D$ com as seguintes séries de equações:

$$
Q=A v, v=\frac{Q}{A}=\frac{Q}{\pi D^2 / 4} \tag{2}
$$

$$
\Delta h=0,0827 \frac{f L_{t o t} Q^2}{D^5} \tag{3}
$$

$$
L_{t o t}=L+L_{e q}=\left(1+L_{e q}^*\right) L \tag{4}
$$

$$
H_{\text {man }}=H_g+\Delta h \tag{5} \label{equ:manometrica}
$$

onde $Q$ é a vazão de projeto, $A$ é a área do tubo, $D$é o diâmetro do tubo, $f$é o fator de atrito da tubulação, $H_{man}$ é a altura manométrica, $L_{eq}^*$ é um fator de aumento no comprimento para incluir perdas localizadas, e $H_g$ é o desnível geométrico do sistema. As equações são válidas para unidades no SI.

Fator de Atrito por Colebrook-White

Um problema surge na equação acima.

O fator de atrito não é constante e depende do tipo de escoamento que o sistema está submetido.

Para determina-lo, poderiamos utilizar o diagrama de Moody.

Nesse exemplo, vamos simplificar o problema e assumir a equação de Coolebrok-White, que pode ser escrita como:

$$
\frac{1}{\sqrt{f}}=-2 \log \frac{\frac{\epsilon / D}{3,7}}{\frac{2,51}{R_e \sqrt{f}}} \tag{6}
$$

A equação acima é implícita e precisa de algoritmos de otimização ou de tentativa e erro para resolve-la.

Na planilha, resolvemo-as automaticamente plotando ambos os lados da equação para diversos valores de $f$ e o ponto de interceptação é o valor do fator de atrito.

Número de Reynolds

Precisamos, no entanto, determinar o número de Reynolds, que é escrito como:

$$
R_e=\frac{\rho v}{\mu} \tag{7}
$$

onde $\rho$ é a massa específica da água na temperatura de projeto e $\mu$ é a viscosidade cinemática da água.

De posse do número de Reynolds, do tipo de tubo e sua rugosidade equivalente, calculamos o fator de atrito.

Depois calculamos a altura manométrica de cada caso para cada diâmetro distinto e determinamos a potência da bomba, como:

$$
P_{\text {motor }}(c v)=1000 \frac{Q H_{\text {man }}}{75 \eta_{b o m b a} \eta_{\text {motor }}} \tag{8}
$$

onde $P_{ot}$ é a potência da bomba em $kW$ e $\eta$ é sua eficiência.

Calculamos assim a potência da bomba para cada diâmetro que estamos testando. Essa potência nos vai servir de base para calcular o custo de energia.

Custos de Implantação e de Energia

Os custos de material são simples.

Basta multiplicar o comprimento total da tubulação pelo custo por metro de tubulação.

No entanto, precisamos transformar esse valor para valor anual equivalente, usando a Eq. \eqref{equ:custos_normalizados}

$$
C_t(D)=C_t(D)^a+C_t^b \tag{9}
$$

Assim, o custo da tubulação é dado por:

onde $C_{t}(D)$ é o custo total de implantação da tubulação de diâmetro $D$, c(D)é o custo por metro de tubulação de diâmetro $D$, e Ct(D) seu custo anual equivalente, já corrigido por $f_a$.

Já o custo de energia pode ser calculado como o total de horas de funcionamento da bomba por ano, multiplicado por sua potência e pelo custo do $kWh$, dado por:

Podemos escrever da seguinte forma:

$$
C_t^b(D)=\operatorname{Pot}(D) * T * 365 * C_e \tag{10}
$$

onde $C_e$ é o custo por $kWh$ de energia consumida, $T$ é o período de funcionamento diário da bomba.

Esse custo já é um custo anual, portanto vamos soma-lo ao valor anualizado do custo do material e, finalmente, vamos obter o custo anualizado do sistema

$$
C_t^s(D)=C_t(D)^a+C_t^b \tag{11}
$$

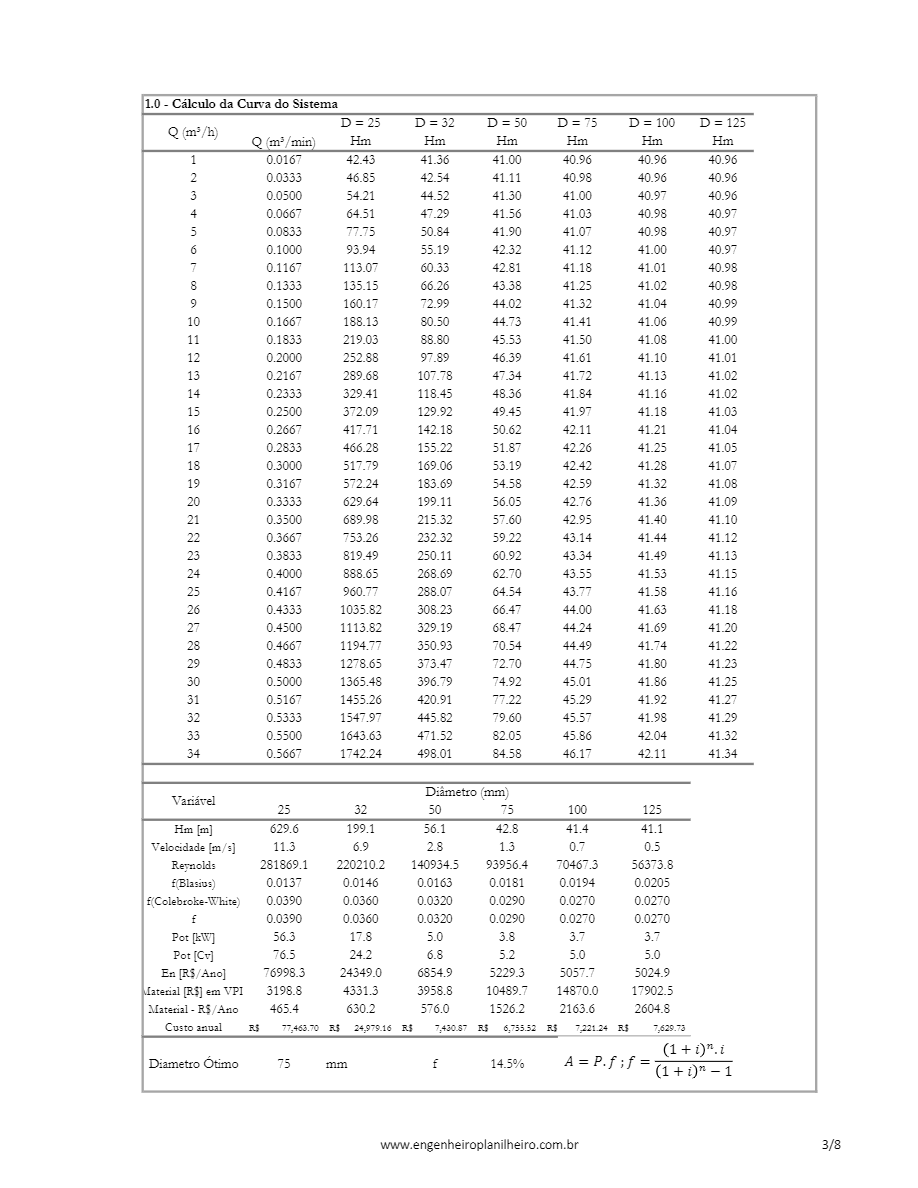
Definição do diâmetro mais econômico

Assim, agora fica fácil de decidir qual sistema é o mais viável em termos econômico-financeiros.

Veja um exemplo disso nessa tabela abaixo:

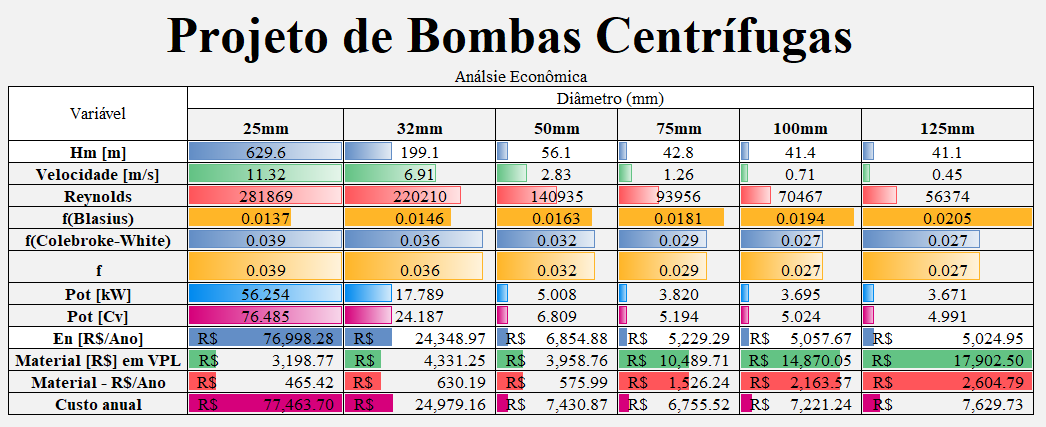
Para os dados do problema acima, o valor ótimo seria o de 75 mm.

Muito bem, vamos imaginar que já sabemos o diâmetro que vamos escolher para a tubulação de recalque.

Agora precisamos dimensionar a bomba para conseguir atender a vazão de projeto para a altura manométrica necessária.

Esse é um problema iterativo.

Testamos algumas famílias de bombas até encontrarmos uma solução que atende as condições de projeto.

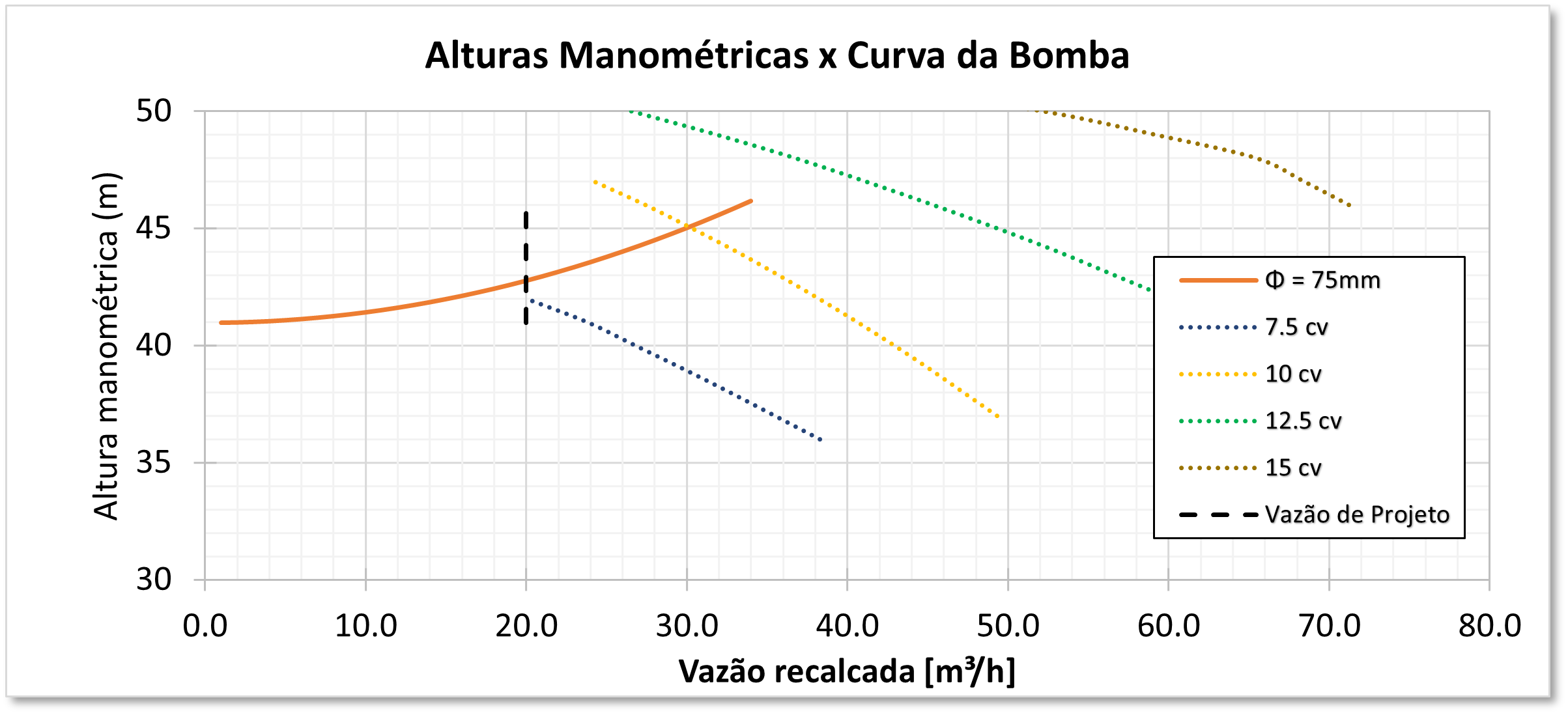
Perceba que, para cada potência da bomba, há uma relação entre vazão recalcada e altura manométrica, isto é, $H = f(Q)$, ou $Q = g(h)$.

Assim, podemos encontrar qual bomba satisfaz nossa vazão e altura recalcada cruzando os gráficos da curva da bomba com os gráficos da curva do sistema.

Mas o que seria essa curva do sistema?

Ela é a curva que indica qual a altura manométrica que o sistema requer para cada vazão recalcada.

Dê uma olhada na equação \eqref{equ:manometrica}.

A curva do sistema é justemante essa equação.

No entanto, anteriormente ela fora escrita somente para a vazão de projeto $Q$.

Se resolvermos ela para diferentes de $Q$ variando desde de $0$ até um determinado valor, conseguimos plotar $H_{\mathrm{man}}$ em função de $Q$ e assim determinar a curva do sistema.

Perceba na imagem acima que a bomba de 7.5 cavalos aproximadamente chega nas condições de projeto requeridas, ou seja, nesse caso uma vazão de $20~m^3/h$.

A bomba de 10 cv também tem um ponto de operação, mas esse ponto recalcaria uma vazão de $30~\mathrm{m^3/h}$

Se nosso reservatório tem um volume $V$ a ser preenchido diariamente, poderíamos usar a bomba de 10 cv caso deixássemos o sistema funcionando por uma duração 2/3T, por exemplo.

No entanto, é importante ressaltar que os custos poderiam mudar.

Vamos focar então na solução com 7,5 cv recalcando aproximadamente $20~\mathrm{m^3/h}$ como solução final de dimensionamento para o sistema de recalque.

As outras bombas não chegaram nem perto das condições de projeto estabelecidas aqui.

É importante notar que você também poderia fazer associações em paralelo ou em série com essa ou com outra família de bombas.

Está finalizada a etapa mais básica do dimensionamento de bombas centrífugas, isto é, a seleção da bomba para o projeto.

Potência do Motor

Outro ponto que passa pelo projeto do sistema moto-bomba é determinar a potência mínima do motor.

Ela pode ser estimada da seguinte forma:

$$
P_{\text {motor }}(c v)=1000 \frac{Q H_{\text {man }}}{75 \eta_{b o m b a} \eta_{\text {motor }}} \tag{12}
$$

onde $\eta_{motor}$ é o rendimento do motor.

Inércia do Sistema Moto-Bomba

O valor da inércia do sistema pode ser fornecida no manual do fabricante da bomba.

Em outros casos, pode-se estimar, de maneira conservadora, o valor de $WR^2$ da bomba e do motor por:

$$
W R_{\text {bomba }}^2=0,03407\left(\frac{P(c v) 0,735499}{N / 1000}\right)^{0,844} ]\tag{13}
$$

onde essas são as inércias mínimas da bomba e do rotor. Mais informações podem ser encontradas aqui. 

Essas inércias são importantes nos cálculos posteriores de golpe de aríete do sistema, detalhado mais adiante no fator $K_b$.

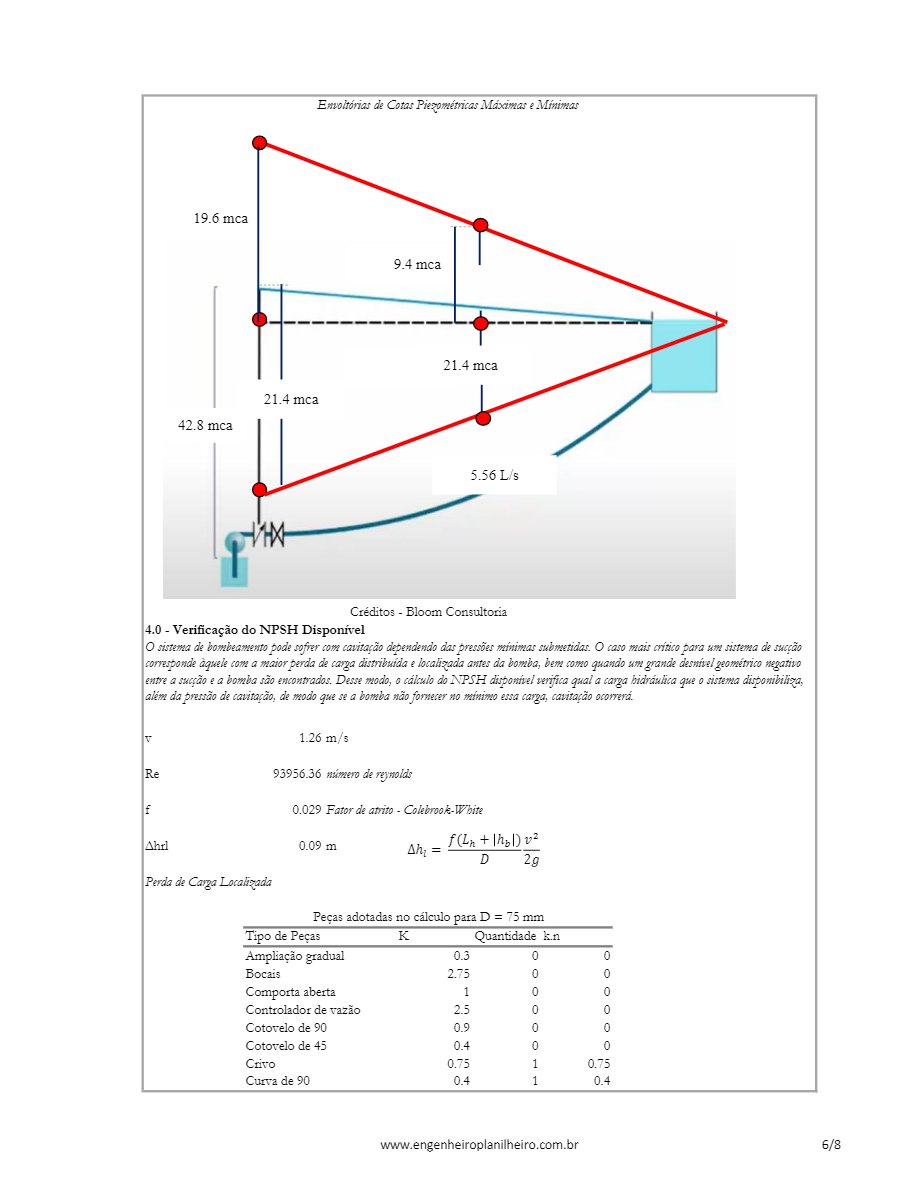
Verificação do NPSH disponível e Requerido

O NPSH, ou Net Positive Suction Head, é a energia mínima que o sistema precisa para evitar que ocorra o fenômeno da cavitação.

Veja o quão dramático é esse fenômeno nesse vídeo:

https://www.youtube.com/watch?v=0dd6AlyOnfc

Precisamos garantir que o sistema de sucção não perca mais energia do que o que há disponível acima da pressão de vapor.

Para isso, devemos minimizar toda e qualquer perda de carga na sucção, evitando curvas de 90 graus e peças necessárias.

O processo de cálculo pode ser dado da seguinte forma:

1. Calculamos as perdas de carga distribuídas desde o ponto de captação até a entrada da bomba
2. Estimamos as perdas de carga localizadas nesse trecho, incluindo todas as peças que o sistema precisa
3. Incluimos no cálculo perdas de carga dinâmicas por troca de diâmetro na tubulação de sucção, caso ocorra
4. Determinamos a pressão atmosférica sabendo-se a elevação ao nível do mar onde encontra-se o sistema elevatório
5. Calculamos a pressão de vapor da água para a temperatura de projeto

A partir de todos os cálculos mencionados anteriormente, o cálculo do NPSH disponível pode ser estimado como:

$$
N P S H_d=\frac{P_a-P_v}{\gamma}-h_b-\sum \Delta h_s-\frac{v^2}{2 g} \tag{14}
$$
onde $\gamma =9,81\rho$, $P_a$ é a pressão atmosférica, $P_v$ é a pressão de vapor, $h_b$ é o desnível geométrico entre o nível do reservatório inferior e a bomba (positivo para bombas elevadas, negativo para bombas afogadas), $\Delta h$ssão perdas localizadas e distribuídas no sistema de sucção, $v$ é a velocidade de sucção.

Caso o NPSH disponível deve superar em 20% o NPSH requerido e ser pelo menos 0,5 mca maior que o NPSH requerido.

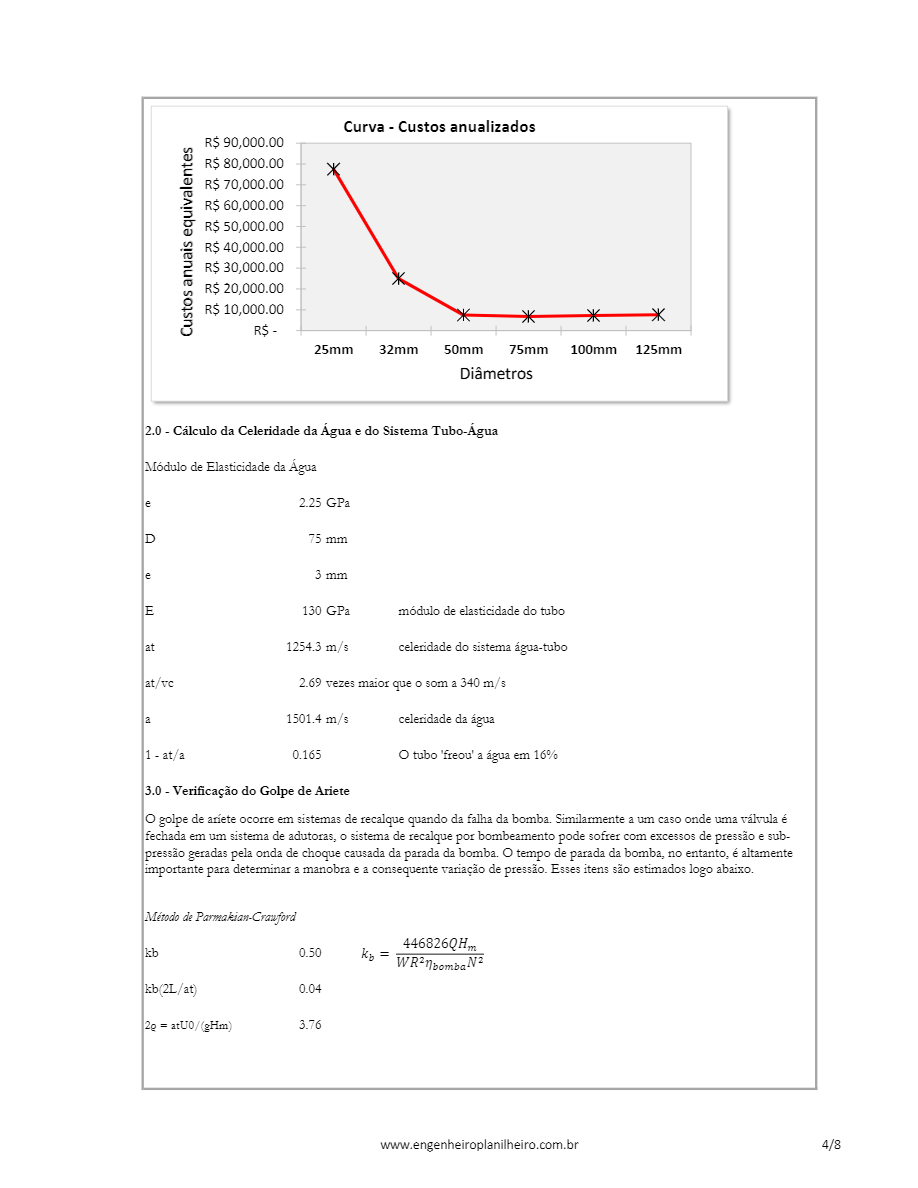
Verificação do Golpe de Ariete

Uma das principais verificações de sistemas elevatórios é o do golpe de ariete no caso de falha imediata do sistema.

Dependendo da inércia do sistema, o tempo de parada da bomba pode variar, o que causa variações de pressão na tubulação de recalque.

Caso seja necessário mais inércia no sistema, a utilização de um volante pode ser feita.

O passo a passo da verificação de golpe de aríete em bombas é dado da seguinte forma:

1. 1. Calcular o módulo de elasticidade da água ($E_w$)
   2. Encontrar o módulo de elasticidade do tubo ($E$)
   3. Determinar a celeridade de água ($a$)
   4. Estimar a celeridade do sistema água-tubo ($a_t$)
   5. Calcular o coeficiente da bomba ($K_b$)
   6. Determinar o parâmetro $K_b$($2L/a_t$)
   7. Determinar $2\rho =a_tv/(gH_{man})$
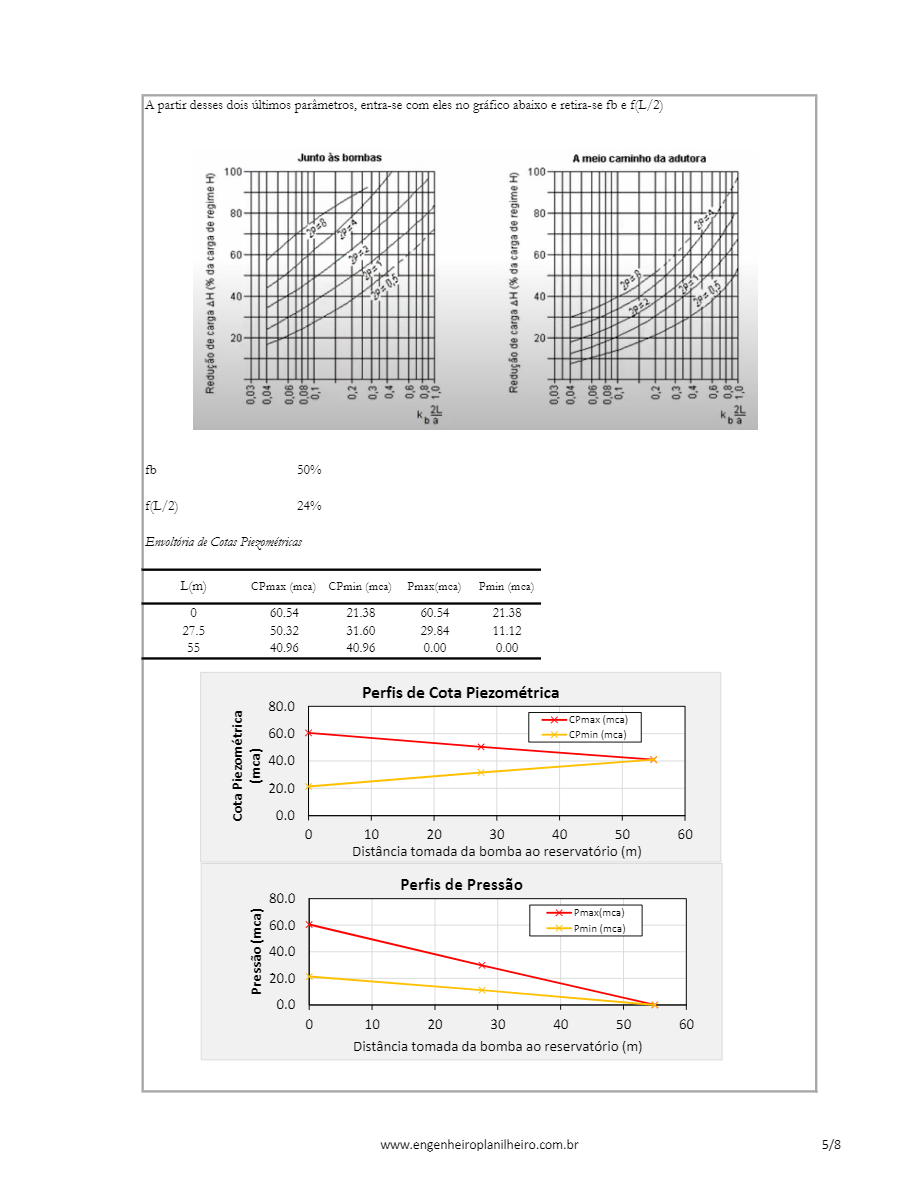
   8. Determinar $f_b$ e $fL/2$, ou seja, os fatores de redução de pressão junto à bomba e à $L/2$ dela
   9. Calcular as envoltórias de cotas piezométricas

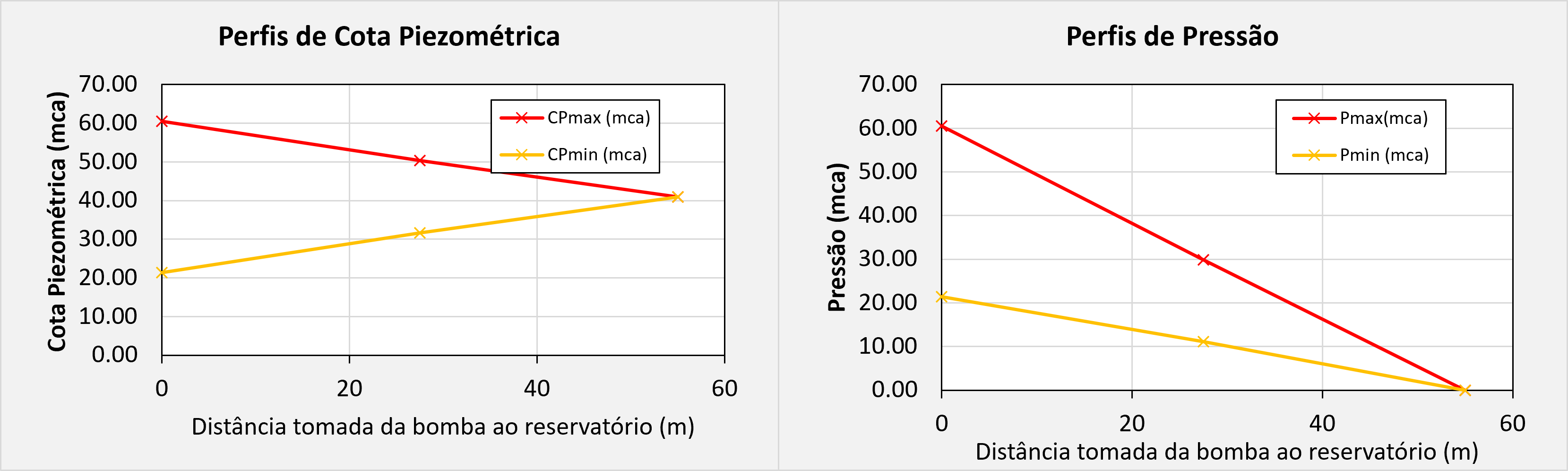
Todas as equações e processos de cálculo para obter o cálculo dos diagramas de pressão na tubulação podem ser encontrados no memorial de cálculo desse problema, anexado ao final desse artigo.

Exemplo – Dimensionamento de Bombas Centrífugas

Quer ver um vídeo mostrando como funciona a planilha? Veja logo abaixo

Ou veja as memórias de cálculo logo aqui abaixo:

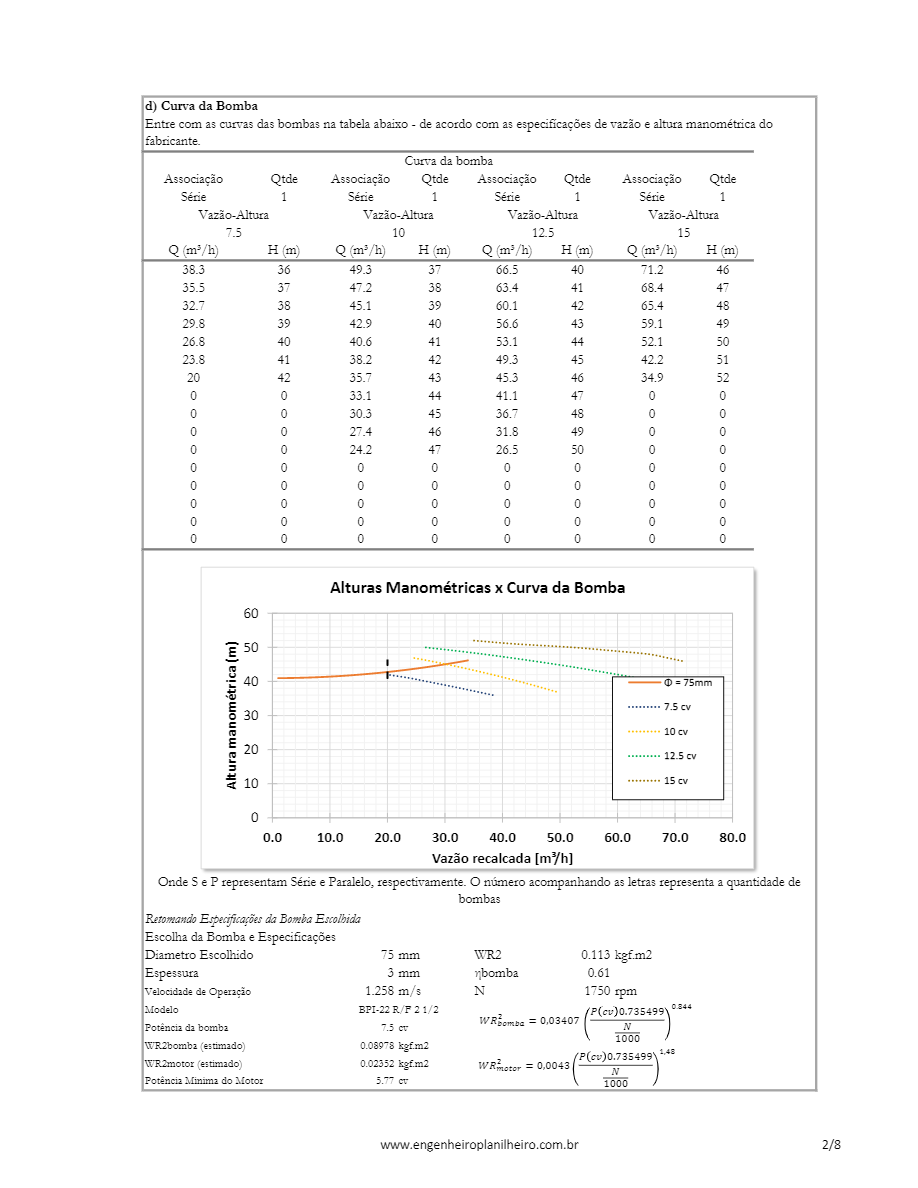
Quer fazer o dimensionamento de bombas centrífugas em 5 minutos e garantir projetos seguros, eficientes e dentro das normas?

Adquira já a planilha! 

Parcelamos em até 12x sem juros!

Entre em contato direto comigo clicando aqui que vou lhe passar todas informaçoes, tirar suas dúvidas e te anteder pessoalmente.

Ou entre em contato pelo whatsapp do meu site que minha equipe também vai lhe atender o mais rápido possível.

Espero que esse texto lhe seja útil!

Um grande abraço,

Marcus.