Redes Malhadas – Hidráulica de Condutos Forçados

As redes hidráulicas são um componente essencial da sociedade moderna, fornecendo água e outros fluidos para residências, empresas e instalações industriais.

A modelagem de redes hidráulicas é uma tarefa crítica que os engenheiros realizam para projetar e analisar sistemas para desempenho ideal.

Os métodos numéricos desempenham um papel vital na modelagem de redes hidráulicas, e uma das técnicas mais utilizadas é o método de Hardy-Cross.

Método Hardy-Cross

O método Hardy-Cross é uma técnica eficiente e robusta para modelagem de redes hidráulicas, porém possui algumas limitações.

Uma das principais limitações é que ele assume o regime de escoamento como quasi-permanente, o que significa que as vazões e pressões na rede são consideradas constantes em cada trecho, ao longo do tempo.

Essa suposição pode não ser válida em algumas situações, como quando há mudanças rápidas na demanda ou quando há flutuações na pressão de abastecimento.

Outra limitação do método de Hardy-Cross é que ele exige que a rede seja dividida em malhas fechadas.

Isso pode ser uma tarefa desafiadora para redes complexas, e a escolha das divisões de loop pode afetar a precisão dos resultados.

Vantagens do Método Hardy-Cross

Apesar dessas limitações, o método Hardy-Cross continua sendo uma ferramenta valiosa para modelagem de redes hidráulicas, principalmente pois pode ser facilmente programada em planilhas eletrônicas.

É fácil de implementar, requer apenas dados básicos de entrada e pode fornecer resultados precisos para a maioria das aplicações.

O método tem sido amplamente utilizado no projeto e análise de sistemas de abastecimento e distribuição de água, bem como em aplicações industriais, como oleodutos e gasodutos.

Este método Foi desenvolvido pelo engenheiro e físico americano Hardy Cross, na década de 1930.

Dr. Cross foi professor na Yale University e seu método desenvolvido revolucionou a forma como estruturas e redes hidráulicas eram dimensionadas na época justamente por ter um método que garantia estabilidade e convergência em poucas iterações.

O método é baseado no princípio de conservação de massa e energia na rede, que implica que o balanço de energia em um anel ou o balanço de massa em cada nó deve zerar.

Detalhes do Método Hardy-Cross

O método Hardy-Cross envolve o uso de um algoritmo iterativo para resolver as vazões e pressões em uma rede hidráulica.

O algoritmo é baseado nos seguintes passos:

a) Atribua vazões arbitrárias a cada tubo na rede, de modo que o balanço nos nós seja igual a 0.

b) Calcule a perda de carga em cada tubo usando a equação de Darcy-Weisbach ou Hazzen-Willians.

c) Estime a perda de carga total em torno de cada malha fechada na rede.

d) Use o princípio de conservação de massa e energia para atualizar as vazões em cada tubo.

e) Repita as etapas b), c) e d) até que as taxas de fluxo convirjam para uma solução estável, isto é, até $\lim_{\Delta Q \rightarrow 0}\Delta Q$ porém com uma vazão nova corrigida, dada por:

$$
\Delta \mathrm{Q}=-\frac{\sum \mathrm{h}_{\mathrm{fa}}}{\mathrm{n} \sum \frac{\mathrm{h}_{\mathrm{fa}}}{\mathrm{Q}_{\mathrm{a}}}} \tag{1}
$$

onde $h_{fa}$ é o somatório de perdas de carga em cada trecho de um anel, $Q_a$ em cada trecho de um anel e $n$ é o expoente da equação de resistência, explicado mais adiante. 

Perdas Distribuídas

Uma forma de calcular as perdas distribuídas é utilizando-se a equação de Darcy-Weisbach.

Ela é uma equação fundamental na mecânica dos fluidos que relaciona a perda de carga em um tubo com a taxa de fluxo, diâmetro do tubo, comprimento do tubo e propriedades do fluido e é dada por:

$$ h_f = f \frac{L}{D} \frac{V^2}{2g} \tag{2} $$

onde $h_f$ é a perda de carga no tubo, $f$ é o fator de atrito, $L$ é o comprimento do tubo, $D$ é o diâmetro do tubo, $V$ é a velocidade do fluxo e $g$ é a aceleração devido à gravidade.

O fator de atrito depende do número de Reynolds, que é uma grandeza adimensional que caracteriza o regime de escoamento na tubulação. Para fluxo laminar, o fator de atrito é dado por:

$$ f = \frac{64}{Re}  \tag{3}$$

onde $Re$ é o número de Reynolds.

Para regime turbulento, o fator de atrito é mais complexo e depende da rugosidade da superfície do tubo, bem como do número de Reynolds.

Nesses casos, podemos usar a fórmula de Swamee, dada por:

$$
f=\left\{\left(\frac{64}{\mathrm{Re}}\right)^8+9,5\left[\operatorname{Ln}\left(\frac{e}{3,7 D}+\frac{5,74}{\mathrm{Re}^{0,9}}\right)-\left(\frac{2500}{\mathrm{Re}}\right)\right]^{-16}\right\}^{0,125} \tag{4}
$$

onde $\epsilon $ é o comprimento da rugosidade do tubo.

Modelagem de Redes usando o software EPANET

EPANET é um software de computador desenvolvido pela Agência de Proteção Ambiental dos EUA (EPA) para modelagem de redes hidráulicas.

Foi primeiramente desenvolvido pelo Eng. Lewis Rossman, também desenvolvedor de outros softwares como o SWMM.

O software usa métodos numéricos para resolver problemas hidráulicos complexos, incluindo aqueles que não podem ser facilmente resolvidos com métodos analíticos tradicionais, como o método de Hardy-Cross.

No entanto, em casos mais simples e em soluções mais rápidas, ainda podemos utilizar de planilhas eletrônicas para a modelagem de redes malhadas.

Modelagem de Redes Malhadas no Excel

Alternativamente aos softwares comerciais, podemos tentar modelar redes complexas usando ferramentas simples como o Excel e o seu Solver numérico.

Nesse item gostaria de mostrar como resolvemos redes malhadas com diversos anéis e vazões consumidas diferentes em cada nó.

Além disso, vou mostrar também como podemos modelar condições específicas como pressões mínimas e máximas que devem ser estabelecidas em cada nó ou vazões e/ou pressões que devem ser constantes a um valor em determinados pontos da rede.

Portanto, é possível também, mesmo utilizando-se de uma ferramenta simples como Excel, modelar redes hidráulicas complexas.

Vamos ver como isso funciona.

Equações de Resistência

De maneira geral, a resistência ao escoamento em um conduto forçado pode ser dada por:

$$
h_f(Q) = k.Q^n \tag{5}
$$

onde os parâmetros $k$ e $n$ são dados pelo modelo de perda de carga distribuída utilizado, descritos na tabela abaixo:

$$
\begin{array}{||c||c|c|c|}
\hline \text { Equação de Resistência } & \text { Relação} & \mathbf{k} & \mathbf{n} \\
\hline \hline \text { Hazen-Williams } & h_f=L \cdot \frac{10.67 Q^{1.85}}{C^{1.85} d^{4.87}} & L \cdot \frac{10.67}{C^{1.85} d^{4.87}} & 1.85 \\
\hline \hline \text { Darcy-Weisbach } & h_f=\frac{8 f L Q^2}{g \pi^2 d^5} & L \cdot \frac{8 f}{g \pi^2 d^5} & \mathbf{2} \\
\hline \hline
\end{array}
$$

onde $L$ é o comprimento da tubulação, $f$ é o fator de atrito, que depende do Número de Reynolds, $C$ é o coeficiente de Hazzen-Willians que caracteriza a perda de carga de acordo com o tipo do material do tubo, $d$ é o diâmetro do tubo e $n$ o expoente da perda de carga.

Assim, dependendo do modelo que utilizamos, sabemos como calcular as perdas usando a fórmula universal ou usando o método de Hazzen-Willians.

Modelagem Hidráulica

Dado a topologia do problema, isto é, como cada nó se conecta, como cada trecho se conecta e liga nós, as retiradas de vazão de cada nó, as saídas de vazão de cada reservatório e as propriedades hidráulicas do fluído e da tubulação, podemos elaborar um modelo hidráulico.

Este modelo basicamente resolve a conservação de energia e de massa em cada nó e em cada trecho, de modo que as cotas piezométricas $CP$ em um nó $j$ que recebe fluxo de um nó $i$ podem ser calculadas da seguinte forma:

$$ \label{equ:rede} CP_i + \Delta h_{i,j} = CP_j,~ CP = \frac{P}{\gamma} + z~~~\forall~\mathrm{i \in \mathbb{E}} \tag{6}$$

onde $\mathbb E$ representa o espaço vetorial dos nós da rede.

Para montar o sistema de equações envolvendo a equação anterior, devemos ser capazes de calcular as perdas em cada trecho e saber as vazões, pelo menos num primeiro momento como estimativas.

Como estimar os sinais da vazão?

Primeiro classificamos os anéis e definimos o sentido horário como positivo.

Perceba que o anel 1 (veja a figura abaixo), da esquerda tem trecho compartilhado (t. 2-5 e t. 5-2).

Assim, a vazão entra como positiva para o trecho 2-5 e entra como negativa para o trecho 5-2.

Perceba também que, por convenção inicial, a vazão no trecho 6-1 é negativa. No trecho 5-6 também, se estivermos seguindo a conveção horária positiva.

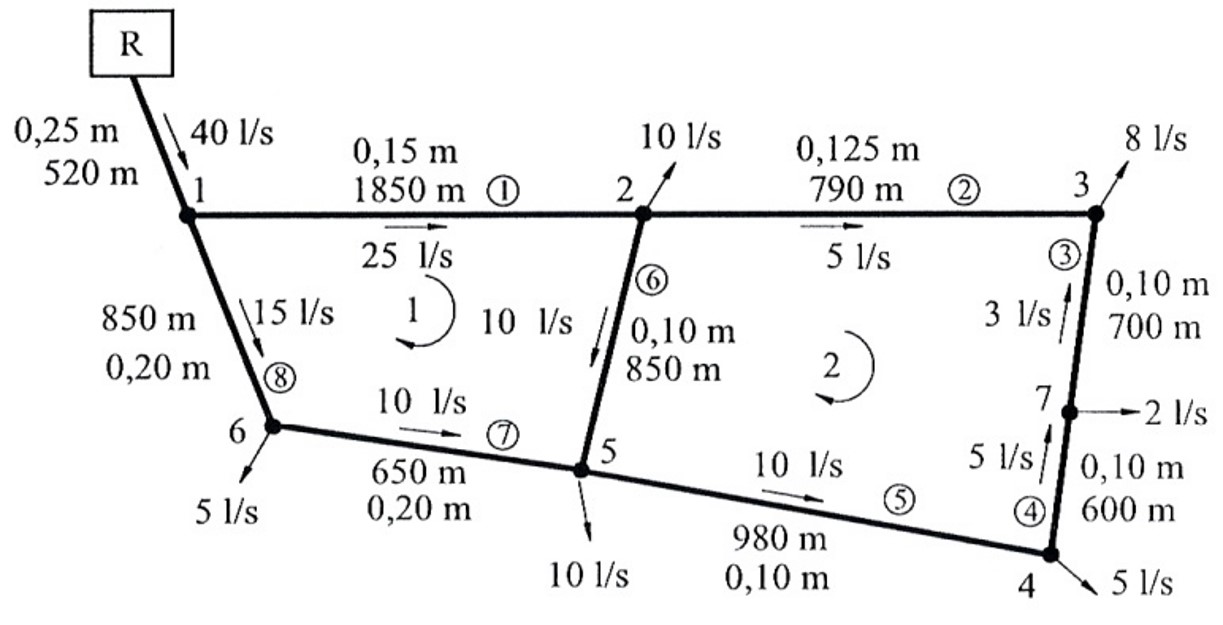
Essas informações da rede podem ser resumidas na planilha nos seguintes dados:

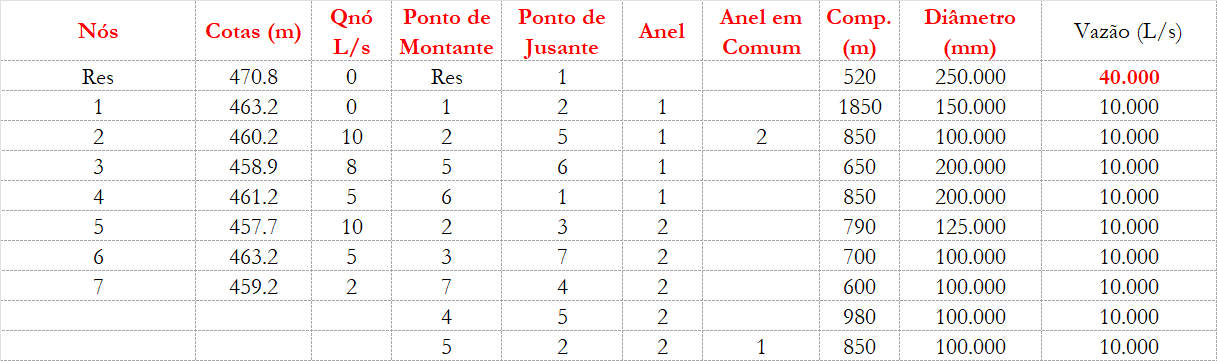
Perceba que classificamos o trecho dizendo a qual anel ele pertence e também se esse mesmo trecho é um trecho compartilhado ou não.

Equações de Conservação de Massa

Em uma rede de distribuição, devemos garantir que o somatório de vazões que entram e saem de um nó é igual a zero.

Quando temos matrizes topológicas que descrevem a conectividade entre trechos, podemos resolver esse balanço de massas como uma multiplicação de uma matriz de direção de fluxo com um vetor de vazões por cada trecho.

No entanto, usando o Excel, esse problema pode ser resolvido usando-se a funçaõ SOMASE ou SUMIF, que basicamente pode servir para somar as vazões que chegam e saem de um determinado nó através de uma coluna com a direção do fluxo.

Assim, a nossa primeira restrição no problema hidráulico é que o somatório dessas vazões em cada um dos nós tem que ser igual a zero, para todos os nós, que pode ser escrita da seguinte forma:

$$
\sum_{i=1}^{n_1} Q_i = 0,~\sum_{i=1}^{n_2} Q_i = 0,~\dots \sum_{i=1}^{n_a} Q_i = 0  \label{equ:vazoes} \tag{7}
$$

onde $a$ é o número de aneis que há na rede, $n_1$ é o número de nós do anel 1, $n_2$ do anel 2, $n_a$ é o número de anéis do último anel da rede e $Q_i$ é a vazão de cada nó do anel.

Restrição de Conservação de Energia em cada Anel

Da mesma forma, de maneira inclusive parecida com as Leis de Kirckoff, fazemos a conservação da energia em cada um dos anéis.

Em outras palavras, se traçarmos um percurso de tubulação que sai de um nó e retorna a este mesmo nó, o somatório de perdas de carga ou, em outras palavras, o somatório do potencial tem que ser nulo.

Assim, escrevemos nossa segunda restrição hidráulica:

$$ \label{equ:pressoes}
\sum_{i=1}^{n_1} h_f^i = 0,~\sum_{i=1}^{n_2} h_f^i = 0,~\dots \sum_{i=1}^{n_a} h_f^i = 0  \tag{8}
$$

onde $a$ é o número de aneis que há na rede, $n_1$ é o número de nós do anel 1, $n_2$ do anel 2 e $h_f^i$ são as pressões em cada nó de cada anel $i$.

Restrição de Vazões Simétricas em Trechos Compartilhados

Em casos com mais de um anel, haverão trechos compartilhados.

Nesses casos, precisamos corrigir as vazões.

Numericamente, podemos imprimir uma restrição hidráulica de modo que a somatória das vazões em trechos compartilhados seja nula.

Ou seja, se imaginarmos que o trecho $i-j$, que faz parte do anel 1 tem vazão $Q$, o trecho $j-i$ que faz parte do anel 2 terá vazão $-Q$.

Assim, imprimimos a seguinte restrição hidráulica:

$$ \label{equ:trechos_comum}
Q_{i,j} + Q_{j,i} = 0, \forall \mathrm{~trechos~em~comum} \tag{9}
$$

Condições de Contorno do Problema

Podemos trabalhar com varias hipóteses.

A mais comum é de fixar uma pressão conhecida no reservatório e verificar as pressões em cada nó da rede.

Outra é usar a altura do reservatório como uma das variáveis de decisão.

Porém, para isso, precisamos definir alguma outra condição para que o problema seja solucionável.

De maneira geral, as variáveis de decisão são (i) as vazões em cada um dos trechos de tubulação e, se necessário, (ii) a altura do reservatório.

As restrições do problema, além das restrições hidráulicas mencionadas em \eqref{equ:vazoes}, \eqref{equ:pressoes} e \eqref{equ:trechos_comum} podem ser:

$$ \label{equ:contorno} \frac{P_k}{\gamma} = c(k)~\mathrm{ou}~,Q_k = q(k) \tag{10}$$

Ou seja, as pressões nos k-ésimos nós são dadas pelos valores $c(k)$ enquanto que as vazões nesses nós são dados por $q(k)$.

Perceba que essas restrições são entradas como retrições de igualdade na formulação do problema de otimização, descrito adiante.

Formulação do Problema de Otimização da Rede

Finalmente, agora podemos formular um problema matemático que determina as pressões, vazões e que, ao mesmo tempo, atenda as restrições hidráulicas do problema, bem como imprima as condições de contorno estabelecidas pelo problema de valor inicial.

Assim, podemos genericamente escrever o seguinte problema de otimização que calcula $\mathbf x = [Q_1, Q_2, \dots Q_n, h_{res}]^T$ ou $\mathbf x = [Q_1, Q_2, \dots Q_n]^T$, onde $n$ é o número de trechos, de modo que:

$$ \min_{\mathbf x}{\sum h_f^1} \\ \mathrm{sujeito~a:}~\eqref{equ:rede}, \eqref{equ:vazoes}, \eqref{equ:pressoes},~\eqref{equ:trechos_comum},~\mathrm{e}~\eqref{equ:contorno}$$

onde $h_f^1$ são as perdas de carga do anel 1.

Exemplo 1) Porto 2006

Determine as vazões de uma rede descrita na Figura 1 e Figura 2 assumindo que a altura no reservatório é uma variável de decisão, bem como as vazões em cada um dos trechos também.

Para isso, utilizaremos a planilha desenolvida por mim. Nela, há uma aba com o nome “Otimização”

Nela, já deixei separado todas as restrições, pressões nos anéis, altura do reservatório e todas outras variáveis que inlfuenciariam o projeto.

Além disso, há um passo a passo lá que explica como utilizar o solver e impor as restrições hidráulicas necessárias, como ilustra a figura abaixo:

Finalmente, precisamos definir a função objetivo, que é de minimização das perdas no anel 1. Ela poderia ser qualquer outra, já que colocamos a somatória de perdas em todos os anéis como 0.

Abaixo a definimos como a minimização da perda no anel 1, mas podemos inclusive ser mais precisos se tentarmos buscar que esse valor atinja a nulidade, como mostra a figura abaixo:

Depois, ajustamos as restrições e as variáveis de decisão. Como temos dois anéis, igualamos cada uma das somatórias de perdas em cada anel a 0.

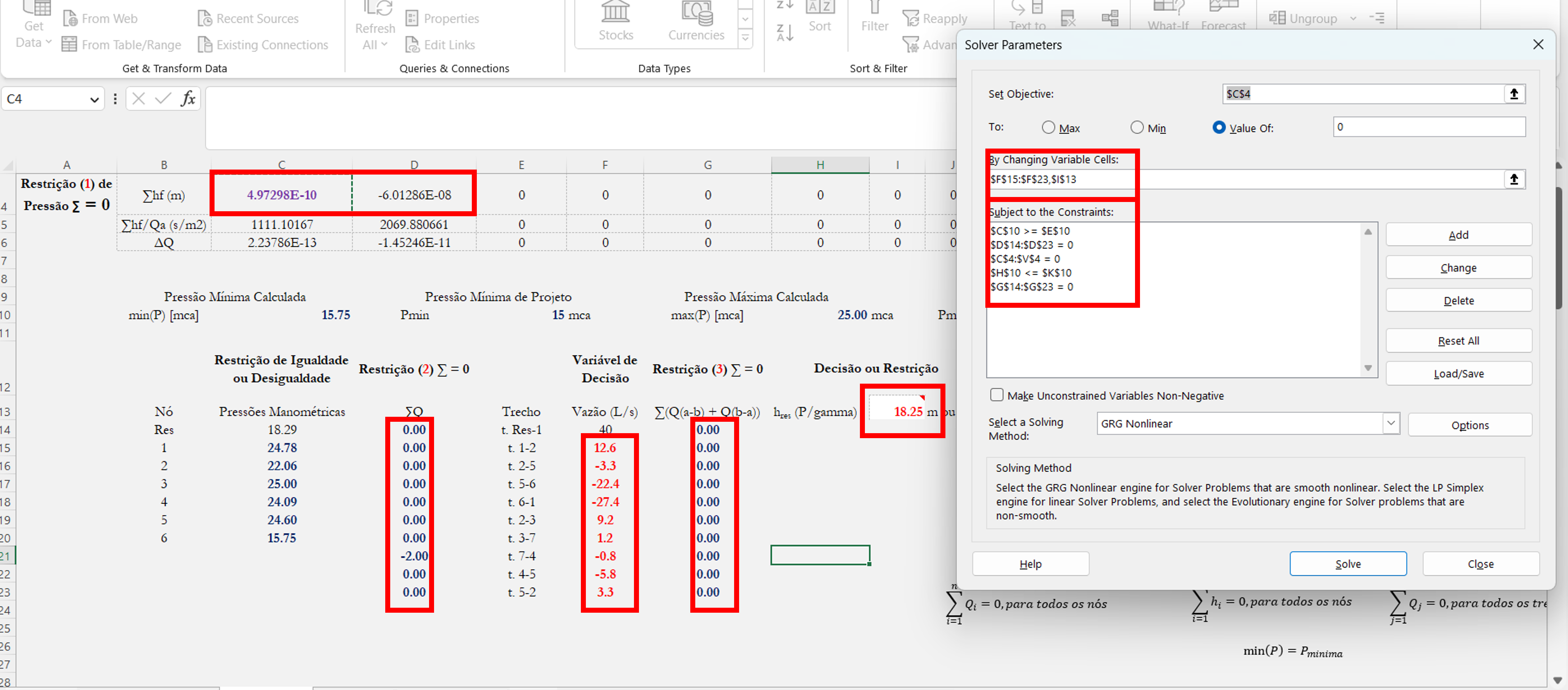
Veja os resultados dessa simulação abaixo. 

pesar de ser meio difícil de ver, basta dar um zoom que é possível captar quais estados estão sendo modelados e quais variáveis o usuário pode ter “mapeada” ao longo da simulação.

Finalmente, os resultados de vazões e pressões podem ser visualizados graficamente, de maneira automática na planilha.

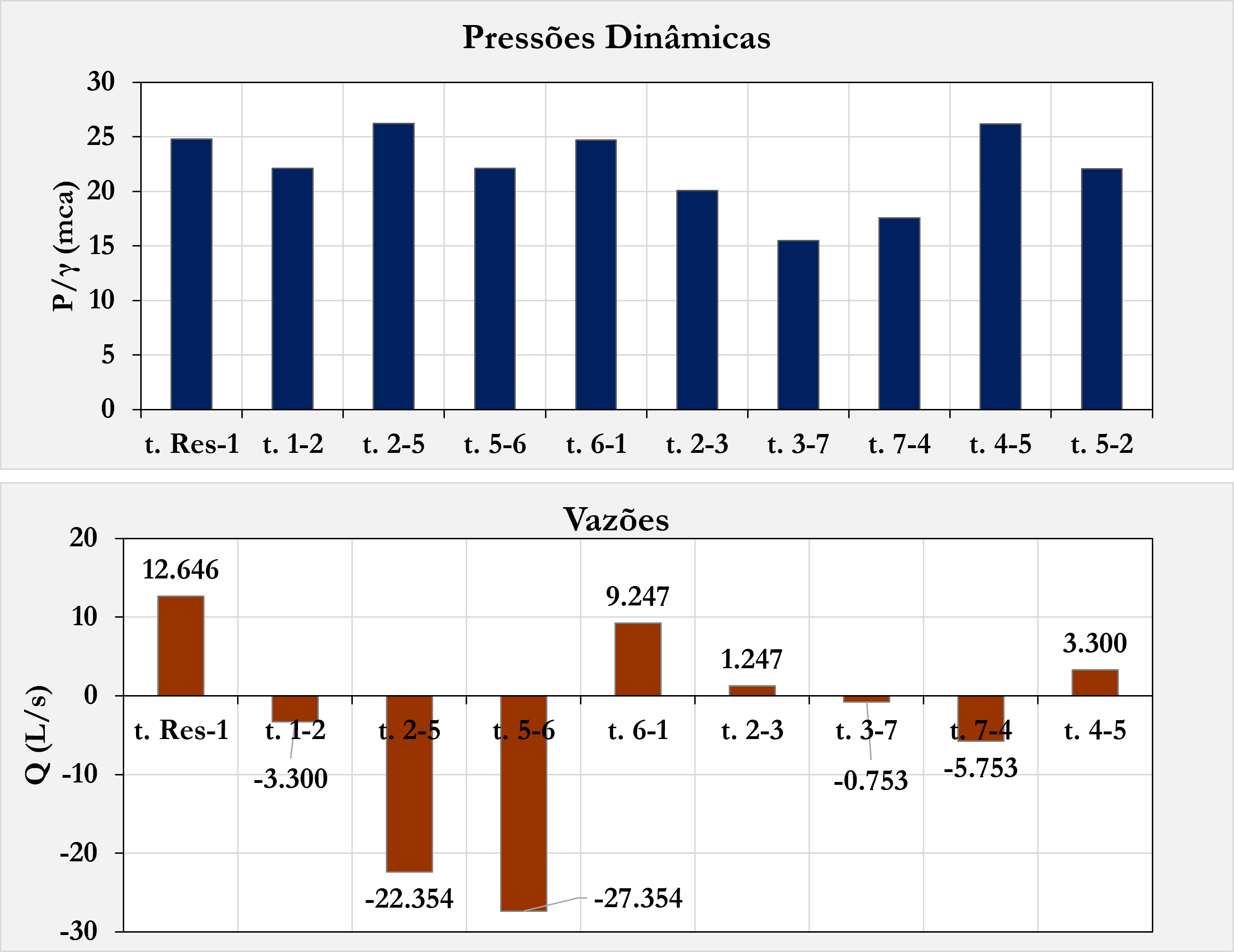
Exemplo)

Vamos agora imaginar que queremos dimensionar a altura do reservatório, de modo que, para as mesmas condições, a pressão no nó 4, provavelmente o nó mais desfavorável, seja exatamente 15 mca.

Além disso, vamos também garantir que as pressões máximas no sistema não ultrapassem 25 mca.

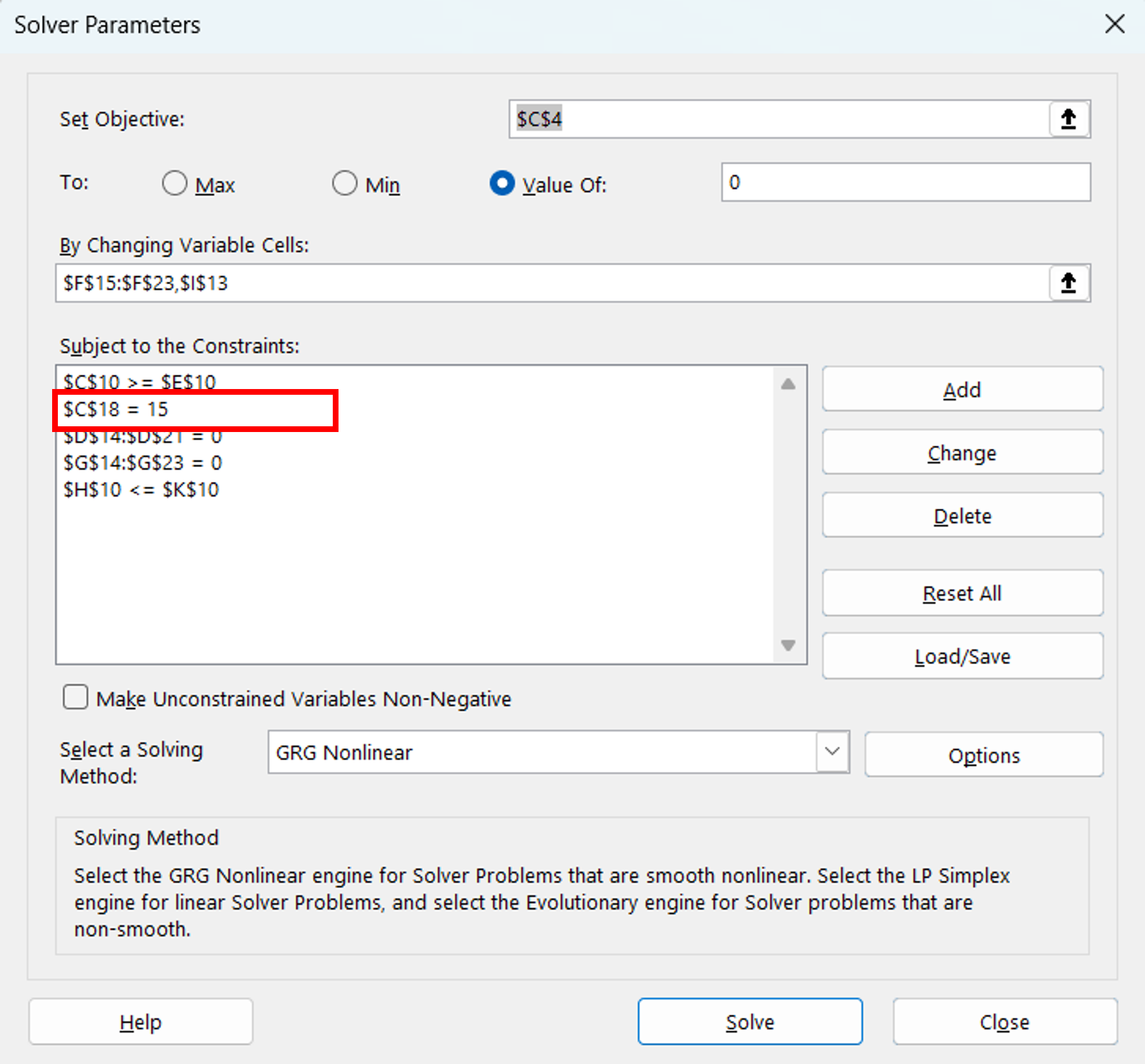
Conclusões

Modelagens numéricas de redes hidráulicas usando o excel requer um entendimento razoável da dinãmica de escoamento em condutos forçados.

Há um universo de possibilidades de dimensionamento e simulação de redes malhadas, aqui mostramos apenas alguns; no entanto, muitos outros ainda podem ser investigados com a planilha desenvolvida.

Nesse artigo mostramos a sua fundamentação teórica e trouxemos alguns exemplos.

Essa planilha que foi utilizada está disponível para compra, juntamente com um mini curso de modelagem de redes hidráulicas, contendo 4 vídeos completos.

É possível sim modelar redes relativamente complexas, com diversos anéis, condições de contorno específicas, vários reservatórios e retiradas e etc mesmo num software simples como o Excel.

É possível sim modelar redes relativamente complexas, com diversos anéis, condições de contorno específicas, vários reservatórios e retiradas e etc mesmo num software simples como o Excel.