Galerias de Águas Pluviais e Sarjetas – Guia Completo de Dimensionamento
Aqui você vai ter um referencial teórico adequado para entender como funciona todo o processo de cálculo de Galerias de Águas Pluviais e Sarjetas.
Tempo de leitura – Aproximadamente 10 minutos.
1 – Introdução ao Cálculo de Galerias Pluviais e Sarjetas
Nesse artigo vamos decorrer sobre Galerias de águas pluviais e Sarjetas e os princípios por trás da modelagem desses elementos.
O ciclo hidrológico, embora reversível, é alterado pela ocupação antrópica da bacia.
Aumento de tempos de concentração, picos elevados no hidrograma e por consequência mais velocidade e aceleração nos escoamentos são alguns dos problemas causados pela não associação do projeto de drenagem de águas pluviais ao projeto de urbanização da cidade.
Aliás, durante muito tempo procurou-se evadir o mais rapidamente as águas do centro para os rios através da adoção de Galerias de Águas Pluviais e Sarjetas. A essa abordagem da-se o nome de visão Higienista, inicialmente preconizada pelo Eng. Saturnino de Brito, no começo do século passado.
Hoje esse conceito tem se modificado e medidas compensatórias estão tomando lugar das medidas corretivas.
Nesse artigo, aprenda os princípios da modelagem de Galerias de Águas Pluviais e Sarjetas que são, ainda, uma das alternativas mais comuns para a coleta e transporte de águas pluviais.
2 – Objetivos dos Sistemas de Drenagem Urbana
Os objetivos do sistema de drenagem convencional são entre outros:
- Reduzir a exposição da população ao risco de inundações,
- Preservar várzeas não urbanizadas, sempre que possível,
- Promover a utilização das áreas de várzeas para atividades de lazer e contemplação com a manutenção das funções ecossistêmicas fluviais e compondo paisagens multifuincionais, etc.
O sistema de drenagem é composto basicamente por dois subsistemas que trabalham em conjunto para alcançar os objetivos expostos anteriormente.
Além disso, esses sistemas podem ser classificados em sistemas de Microdrenagem e Macrodrenagem.
A eventual falha desses sistemas ocasiona inundações urbanas, cada um com uma certa escala.
Falhas de microdrenagem provocam problemas mais localizados.
Falhas de macrodrenagem, por sua vez, provocam problemas em uma escala maior, geralmente devido ao extravazamento de um curso d’água, por exemplo.
As falhas podem ser classificadas como alagamentos, que são associados à microdrenagem. Uma boca de lobo que entupiu, ou uma galeria sub-dimensionada são exemplos disso.
Já as Inundações são associadas à macrodrenagem, especialmente quando há o extravasamento de rios e canais, podendo até atingir áreas extensas e durar longos períodos.
As Enxurradas, por outro lado, são eventos associados à macrodrenagem, porém com características de maior velocidade e grande poder de destruição. Estas geralmente ocorre em vales fluviais com alta declividade.
3 – Riscos de Projeto, Elementos dos Sistemas e Chuvas de Projetos
Os elementos da microdrenagem em geral são: (i) lotes urbanos, praças, ruas, galerias, sarjetas, bocas de lobo, sarjetões, etc.
O risco de falha admitido a esses sistemas pode variar de acordo com a norma vigente no município.
Além disso, este valor encontra-se, geralmente, na faixa de Tempos de Retorno da ordem de 2 a 10 anos.
Os elementos da macrodrenagem são: Hidrografia natural e canais de drenagem.
Esses elementos recebem as águas da microdrenagem, que pode incorporar diversas sub-bacias.
O risco admitido a esse sistema geralmente varia entre 10 e 100 anos, ou seja, admite-se pelo menos uma falha, em média, a cada 10 ou 100 anos.
No Brasil, usualmente adota-se 25 anos [Ministério das cidades, 2012].
3.1 – Chuvas de Projeto
A definição da chuva corrente de projeto deve ser tal que o sistema tenha plena capacidade de resposta tanto ao volume precipitado quanto a sua intensidade.
Os principais aspectos da determinação da chuva de projeto são: área de abrangência da tormenta, tempo de duração da chuva e probabilidade de ocorrência, de modo que:
- A intensidade da chuva é diretamente proporcional ao tempo de recorrência;
- Além disso, é inversamente proporcional à duração da chuva;
- Por fim, decai exponencialmente à medida que a área aumenta devido a efeito de distribuição espacial da chuva.
Desse modo, a primeira decisão a ser tomada, refere-se ao nível de segurança exigido no projeto.
3.2 – Tempo de Recorrência
O tempo de recorrência de uma chuva é definido como o período de tempo em que um determinado evento poderá ser igualado ou superado, ao menos uma vez, sendo relacionado à frequência de ocorrência desse evento, segundo a equação:
$$
TR = \frac{1}{f} \tag{1}
$$
Em que:
$TR$: tempo de recorrência (anos)
$f$ : frequência ou probabilidade de ocorrência do evento TR em um ano
3.3 – Risco de Falha em Projetos de Galerias de Águas Pluviais e Sarjetas
De acordo com a vida útil de projeto, a probabilidade do sistema falhar pode ser calculada pela equação:
$$
P_{TR}^n = 1 – (1 – 1/TR)^n
$$
Em que:
$n$ é o número de anos do período em análise, eventualmente podendo ser a vida útil do projeto.
Perceba que um tempo de retorno de 25 anos, em uma vida útil de 20 anos, há uma chance de 56% de haver ao menos um evento maior que o evento de projeto.
Desse modo, após ser definido o risco de falha do projeto, deve ser definida a duração da chuva.
3.4 – Duração da Chuva
Chuvas com curta duração tendem a provocar maiores picos de vazão na rede de drenagem, enquanto que chuvas mais longas resultam em um hidrograma mais distribuído, porém com um maior volume.
Sendo assim, a duração da chuva deve ser definida de acordo com o tipo de dispositivo a ser utilizado.
No projeto de galerias e canais é usual adotar a duração da chuva como igual ao tempo de concentração da bacia em estudo.
Essa é a condição crítica para o dimensionamento da rede pois toda bacia estará contribuindo no menor tempo de chuva possível, o que acarreta uma maior intensidade de precipitação.
O último parâmetro deve ser a área de ocorrência da precipitação.
Estudos indicam que as chuvas possuem uma distribuição espacial na qual sua intensidade diminui à medida que se afasta do núcleo central de precipitação.
Desse modo, podemos considerar o decaimento da intensidade da chuva caso a área de drenagem seja muito grande.
4 – Dimensionamento do sistema de de Microdrenagem Urbana – Galerias de Águas Pluviais + Sarjetas
Esta seção trata dos equacionamentos necessários para o correto dimensionamento de sarjetas e galerias de águas pluviais.
4.1 Sarjetas e Bocas de Lobo
O dimensionamento das sarjetas é o primeiro passo da rede de microdrenagem. A vazão pode ser calculada pela equação de Manning-Strickler, dada por:
$$
Q(t) = \frac{1}{n}R(y_0)^{2/3}.A(y_0).S_0^{1/2} \tag{2}
$$
$R$ é o raio hidráulico da seção de projeto, dado pela razão entre a área molhada pelo perímetro molhado [m], $A$ é a área molhada na seção transversal [m2], $S_0$ é a declividade normal da seção em [m/m], $y_0$ é a altura d’água na galeria, e $n$ é o coeficiente de rugosidade médio da seção.
Eventualmente deve ser adicionado um fator que explique a obstrução das sarjetas. Em contrapartida pode ser adotado um coeficiente de Manning maior.
A definição da geometria da sarjeta varia de acordo com a norma vigente do município; a velocidade máxima e mínima também.
Uma prática razoável para determinar a largura da sarjeta é definir uma tal que seja possível uma pessoa comum passar sobre a sarjeta com um passo, sem pisar na água.
Quando a vazão calculada for maior que a capacidade da sarjeta, é necessária a instalação de bocas de lobo ou caixas ralo.
O Departamento Nacional de Infraestrutura de Transporte (DNIT) apresenta os detalhamentos básicos de bocas de lobo combinadas, bocas de lobo simples, bocas de lobo simples com grelha de concreto e bocas de lobo duplas com grelhas de concreto.
Analogamente as sarjetas, as bocas de lobo devem também considerar uma perda na capacidade hidráulica, ocasionada por possíveis obstruções ou irregularidades nos pavimentos das ruas junto às sarjetas e ao alinhamento real.
A (CETESB/DAEE, 1989) apresenta uma tabela de redução de capacidade para bocas de lobo.
| Localização da sarjeta | Tipo de boca de lobo | % permitida sobre o valor teórico |
| Ponto baixo | De guia | 80 |
| Com grelha | 50 | |
| Combinada | 65 | |
| Ponto intermediário | De guia | 80 |
| Grelha longitudinal | 60 | |
| Grelha transversal ou longitudinal com barras transversais combinadas | 60 |
4.1.1 – Cálculo do espaçamento entre bocas de lobo.
1) Cálculo da área de captação (A) pelo método racional
$$
Q(t) = C \times I(t) \times A \rightarrow A = \frac{Q(t)}{C \times I} \tag{3}
$$
Onde:
$Q$ é a vazão, $C$ é o coeficiente de runoff e $i$ a intensidade crítica de projeto.
A área A pode incluir tanto áreas relativas ao greide e calçadas, quanto áreas relativas as edificações à montante do trecho em estudo.
2) Cálculo da área de captação pela geometria da rua
Nesse caso, vamos assumir que a sarjeta colete apenas a área de metade da rua, sem considerar a calçada.
$$
A = \frac{L_r}{2}\Delta x \tag{4}
$$
Onde:
$A$: área em m²;
$L_r$ largura da rua em m;
$\Delta x$ espaçamento entre dispositivos em m;
Para determinar o comprimento máximo entre bocas de lobo no caso onde sarjetas coletam apenas a rua, basta igualar as duas equações anteriores e determinar o espaçamento mínimo.
Já no caso que a sarjeta colete mais área que a área da rua, basta escrever uma função para essa área e igualar com a equação do método racional.
4.2 – Galeria de Águas Pluviais
Galerias de Águas Pluviais são tubulações de seção e declividade conhecidas que tem por objetivo coletar e transportar o escoamento superficial gerado por ruas, edificações, áreas impermeáveis como estacionamentos, pátios e inclusive podem também coletar água proveniente do excesso de precipitação em áreas permeáveis.
Os critérios básicos de projeto são apresentados abaixo:
4.2.1 Diâmetro mínimo das tubulações das galerias de águas pluviais
O diâmetro mínimo das tubulações depende das normas vigentes e do material utilizado para o projeto das galerias.
De maneira geral, o diâmetro mínimo, especialmente para tubulações de concreto e pead são de:
$$
D_{\mathrm{min}} = 0.40~m \tag{5}
$$
4.2.2 Velocidades máxima e mínima de Galerias de Águas Pluviais
As velocidades máximas devem levar em conta a possibilidade do desprendimento do material de fundo devido as altas tensões de cisalhamento causadas na superfície do tubo em casos onde a velocidade é elevada.
Desse modo, cada material tem sua especificação. Além disso, manuais vigentes usualmente recomendam os critérios restritivos de velocidade máxima.
Abaixo segue uma recomendação geral.
Em relação à velocidade mínima, deve-se ter em mente que velocidades demasiadamente baixas favorecem o acúmulo de detritos e sedimentos no interior dos tubos.
Assim, é recomendável aplicar uma velocidade mínima no dimensionamento.
$$
V_{\mathrm{max}} = 5~\mathrm{m/s} ~ e~V_{\mathrm{min}} = 0.75~\mathrm{m/s} \tag{6}
$$
4.2.3 Mudanças de diâmetro em Galerias de Águas Pluviais
- Tubos alinhados pela geratriz superior evitando assim verificação de remanso.
4.2.4 Escoamento superficial livre e enchimento máximo:
Uma ideia relativemente errada é pensar que um tubo circular cheio tem mais vazão que um tubo circular com certa borda livre.
Na verdade, o aumento da área molhada, a partir de certo ponto, é menor que o aumento do perímetro molhado para uma seção circular.
Isso faz com que uma seção com menos lâmina d’água tenha mais capacidade de vazão que uma seção mais cheia.
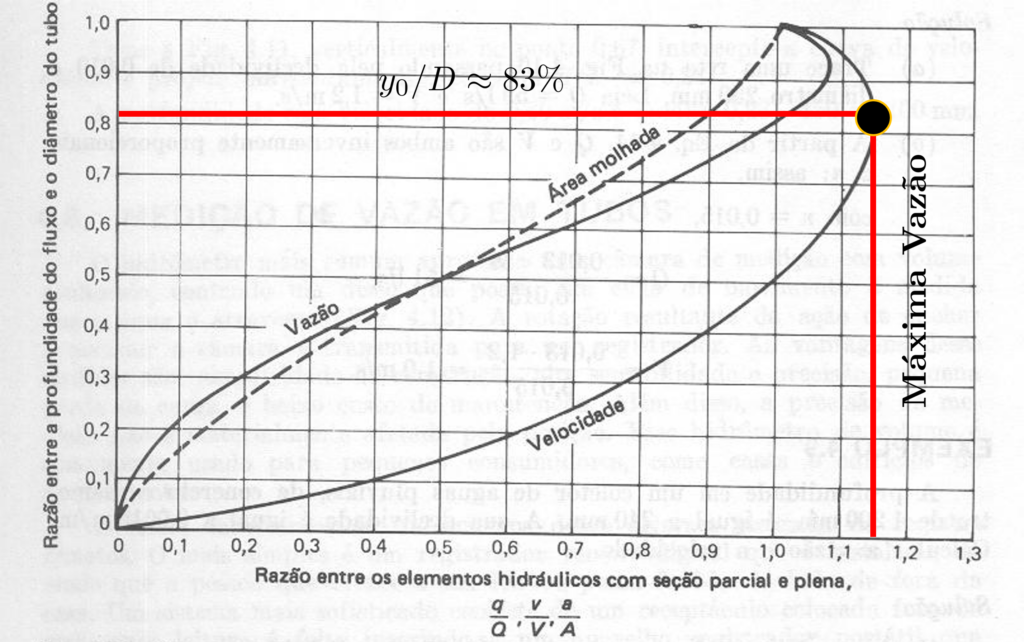
Lâmina líquina ($y/D$) < 85%
4.2.5 Etapas Fundamentais do Projeto de Drenagem Urbana: Galerias de Águas Pluviais e Sarjetas
Antes de iniciar o projeto, é necessário o levantamento de três informações básicas:
- Topografia: Definição das bacias principais, onde estão as maiores linhas de drenagem e as bacias locais, bem como definir os escoamentos da água.
- Traçado urbano proposto ou existente: O traçado urbano combina-se com e modifica o desenho topográfico original, dando contornos particulares a cada região que precisa receber a drenagem.
- Pluviometria: Identificação de equações intensidade x duração x frequência (IDF) para as chuvas, com objetivo de elaborar as chuvas de projeto
As etapas de projeto são:
1ª: Análise da área de implantação do projeto, incluindo o reconhecimento local e levantamento topográfico para traçado da rede em planta.
2ª: Definição do tempo de recorrência (TR) da chuva de projeto, para a qual será dimensionada a rede.
3ª: Escolha da equação intensidade-duração-frequência (IDF) aplicável a região em estudo, para o período de retorno escolhido.
4ª: Definição das áreas de contribuição em cada seção de cálculo, geralmente onde estão localizados os poços de visita.
5ª: Determinação do coeficiente de escoamento médio, $C = \sum_{i=1}^{n_p} C_i . A_i / \sum_{i=1}^{n_p} A_i$, ponderado para a área de contribuição, em cada seção de cálculo: , onde i representa uma sub-bacia que se liga ao Pvi.
6ª: Determinação do tempo de concentração para cada trecho.
7ª: Determinação da intensidade média de precipitação para duração igual ao tempo de concentração do trecho, utilizando a IDF escolhida.
8ª: Cálculo da vazão de projeto do trecho, por aplicação da equação do método racional modificado.
9ª: Definição do diâmetro e da declividade do trecho de galeria, considerando a minimização de custos, aspectos técnicos e regulamentares de implantação, como recobrimento mínimo, e satisfação dos critérios hidráulicos (capacidade de escoamento, enchimento e velocidade máximos).
10ª: Determinação do tempo de percurso ao longo do trecho, considerando a extensão da galeria e a velocidade média do escoamento, para vazão de projeto.
11ª: Adição do tempo de percurso calculado na etapa anterior ao tempo de concentração calculado na sexta etapa.
12ª: Repetição para todos os trechos de todos os passos de cálculo, de montante para jusante, a partir da quinta etapa.
Para execução dos passos acima, elabora-se planilhas de cálculo para efetuar todas as condições propostas como a apresentada no próximo tópico.
5 – Planilha em Exel para Cálculo de Galerias e Sarjetas Pluviais
Devido a alta complexidades e calculos intertravados entre cada sub-trecho de galeria, usualmente constrói-se planilhas para auxiliar o projeto de redes de drenagem.
A planilha é subdivida em seções como
- Poços de visita,
- Deflúvio a escoar para jusante,
- Galeria de jusante e Sarjetas.
Dados de entrada são apresentados em colunas em vermelho
Além disso, na parte superior da planilha há a inserção de dados pluviométricos e condições de dimensionamento das galerias e sarjetas.
As etapas e execuções da planilha serão discutidas a seguir.

5.1 – Parâmetros de projeto – Galerias de Águas Pluviais
Condições normativas previstas pelo município e parâmetros hidráulicos para o dimensionamento.

5.2 – Parâmetros de projeto – Sarjetas
Condições hidráulicas para o dimensionamento das sarjetas.

5.3 – Seção – Poços de Visita
Na aba Locação, são inseridos a numeração e a estaca do poço de visita de referência.
Na aba Cotas no poço são insere-se as cotas do greide onde se localiza o poço de visita. Quatro cotas são indicadas em cada poço de vista sendo estas:

5.3.1 – Cálculo para poços de visita sem galerias de montante:
- Cota de fundo de entrada: A cota de fundo de entrada é nula, pois não há entrada de galeria de montante.
- NA entrada: O nível d’água também é nulo.
- Cota de fundo de saída: A cota de fundo de saída é igual a soma do recobrimento mínimo com o diâmetro da galeria de jusante
$$
CF_{saída(PV_{\mathrm{ponta-seca}}} = Rec_{\mathrm{min}} + \phi_{\mathrm{jusante}} \tag{7}
$$
Onde $Rec_{\mathrm{min}}$ é o recobrimento mínimo da tubulação
- NA saída: O nível d’água de saída do PV é igual a soma da cota de fundo de saída com o tirante normal do trecho de galeria.
$$
NA_{\mathrm{saída}} = CF_{\mathrm{saída(PV_{ponta-seca})}} + y_0 \tag{8}
$$
Onde $y_0$ é a lâmina d’água.
5.3.2 – Cálculo para poços de visita com galerias de montante:
- Cota de fundo de entrada: A cota de fundo de entrada no PV(i + 1) é igual a cota de fundo de saída do PV(i) subtraída do produto entre a declividade do trecho (i ao i+1) e o comprimento do trecho (i ao i+1), matematicamente escreve-se:
$$
CF_{\mathrm{entrada(PV_{i+1})}} = CF_{\mathrm{saida(PV_i)}} + s_0(t.~i \rightarrow i+1) \times L_{t.~i \rightarrow i+1} \tag{9}
$$
Em que:
$s_0$: Declividade do trecho em m/m
$L$: Comprimento do trecho em m
5.3.3 – Nível d’água
- NA entrada: O nível d’água de entrada é igual a cota de fundo de entrada no PV(i+1) somado ao tirante normal do trecho (i ao i+1)
- $$
NA_{\mathrm{entrada(PV_{i+1})}} = CF_{\mathrm{entrada(PV_{i+1})}} + y_{\mathrm{0,(i \rightarrow i+1)}} \tag{10}
$$5.3.4 – Cotas de Fundo
- Cota de fundo de saída: A cota de fundo de saída é a soma entre a cota de fundo de entrada com a diferença dos diâmetros, sendo o diâmetro de jusante no mínimo igual ao diâmetro de montante.
$$
CF_{\mathrm{saída(PV_{i+1})}} = CF_{\mathrm{entrada(PV_{i+1})}} + \Delta \phi \tag{11}
$$Em que:
$\Delta \phi$ é o módulo da diferença algébrica dos diâmetros de jusante e de montante do PV em estudo.
- NA saída: O nível d’água de saída é igual à soma entre a cota de fundo e o tirante normal desenvolvido no trecho a jusante do PV em estudo
$$
NA_{\mathrm{saida(PV_{i+1})}} = CF_{\mathrm{saída(PV_{i+1})}} + y_{0,i \rightarrow i+1} \tag{12}
$$5.3.5 – Recobrimento
Recobrimento mínimo: A norma vigente no Rio de Janeiro recomenda que o recobrimento mínimo deve ser:
$$
Rec_{\mathrm{min}} = 0.4 + \phi/2 \tag{13}
$$
5.4 – Defluvio a escoar para jusante
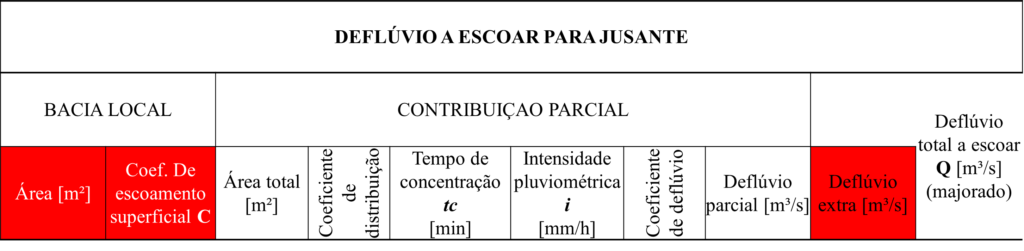
5.4.1 – Aba Bacia Local
- Área: A cidade é dividida em quarteirões e bacias são divididas em sub-bacias de modo que haja uma área de drenagem em cada trecho entre poços de visita. Portanto essa área é obtida do levantamento planimétrico.
- Coeficiente de escoamento superficial (C): A partir do zoneamento da cidade é obtido o valor médio do coeficiente de runoff, que varia muito rapidamente com o uso e ocupação do solo e entre outros fatores.
- Defúvio extra: Caso haja um deflúvio que venha de outra rede ou que o usuário deseje acrescentar no trecho, pode-se preencher esse valor nessa coluna.
5.4.2 – ABA – Contribuição Parcial
- A área total é obtida pela área da bacia local do PV em estudo, somado as áreas ou a área proveniente dos PVs ou PV de montante. No caso de PVs que trabalham como pontas secas, a área total é igual a área da bacia local.
- Coeficiente de distribuição: Coeficiente que considera a distribuição não equivalente da chuva em uma bacia hidrográfica de grandes dimensões. É calculado como:
$$
\begin{align}
C_d &= 1,~ \text{se}~ A \leq 10.000~\mathrm{m^2} \\
C_d &= \frac{A}{10.000}^{-0.15}~\text{se}~A > 10.000~\mathrm{m^2} \rightarrow \text{Decaimento exponencial} \tag{14}
\end{align}
$$
5.4.2.1 – Tempo de Concentração
- Tempo de concentração (tc) [min]: Existem inúmeros estudos e equações para a determinação do tempo de concentração de uma bacia, dentre elas destaca-se a equação de Kerby.
$$
t_c = t_1 + t_2 \tag{15}
$$
Em que:
$t_1$ é tempo de percurso sobre escoamento natural (tempo de entrada)
$t_2$ é o tempo de percurso sobre talvegues bem definidos
Para o primeiro poço de visita, o tempo de concentração é igual ao tempo de entrada.
Esse, pela equação de Kerby pode ser calculado como:
$$
t_1 = 1.44 \left(L_2.C_k \left( \frac{1}{S_{2}^{0.5}} \right)\right)^{0.47} \tag{16}
$$
Onde $L_2$ é a distância média de escoamento superficial até a chegada do PV e $S_2$ a declividade média da região superficial até o PV.
| Tipo de superfície | Coeficiente $C_k$ |
| Lisa e impermeável | 0,02 |
| Terreno endurecido e desnudo | 0,10 |
| Pasto ralo, terreno cultivado em fileiras e superfície desnuda | 0,20 |
| Pasto ou vegetação arbustiva | 0,40 |
| Mata ou árvores decíduas | 0,60 |
| Mata de árvores decíduas tendo solo recoberto por espessa camada de detritos vegetais | 0,8 |
Geralmente, o tempo de entrada pode ser estimado em 5-10 minutos.
O tempo é igual ao tempo de percurso, desenvolvido no trecho de galeria pela divisão entre a distância do trecho e a velocidade média de percurso.
$$
t_2 = \frac{L}{v} \tag{17}
$$
A velocidade será definida posteriormente.
5.4.2.2 – Intensidade de Chuva
- Intensidade pluviométrica: Valor da chuva de projeto para o trecho de galeria a ser dimensionado. É importante observar que a chuva de projeto varia de acordo com o tempo de concentração. Portanto haverá chuvas diferentes para trechos de galerias diferentes.
$$
i = a\frac{TR^n}{(t_d + b)^{m}} \tag{18}
$$
TR, a, b e m são parâmetros já definidos anteriormente.
- Coeficiente de deflúvio: Coeficiente utilizado para corrigir a tendência do método racional em superestimar as vazões de pico. Esse coeficiente pode ser estimado pelo critério de Fantolli por meio da seguinte equação:
$$
f = 0.0725.C.(i.t)^{1/3} \tag{19}
$$
Em que:
C: coeficiente de runoff
i: intensidade pluviométrica [mm/h]
t: tempo de concentração [min]
5.4.2.3 – Deflúvio Parcial
- Deflúvio Parcial: Vazão de projeto em m³/s, resultante da chuva sobre a bacia de contribuição local, calculada pelo método racional modificado, multiplicando o coeficiente de deflúvio, coeficiente de distribuição, coeficiente de runoff, intensidade pluviométrica e área local.
$$
Q(t) = f.C_d.C \left ( \frac{i(t)}{3.6 \times 10^6} \right )A \tag{20}
$$
i: [mm/h]
A: [m²]
5.4.2.4 – Deflúvio Total
- Deflúvio total a escoar: O deflúvio total a escoar será igual ao deflúvio parcial se o poço de vista for do tipo ponta seca. Se não, será a soma do deflúvio parcial do trecho, acrescido do deflúvio total do trecho de montante.
Ponta seca:
$$
Q_t = Q \tag{21}
$$
Trecho de montante contribuinte:
$$
Q_{t,PV_{i+1}} = Q + Q_{t,PV_i} \tag{22}
$$
5.4.3 – ABA – Galeria de Jusante
- Trechos entre PVS: A nomenclatura adotada para os trechos é do tipo:
$t.~m-n$
Em que:
m: Numeração do PV de montante
n : Numeração do PV de jusante
- Declividade S: Definida como a razão entre o desnível entre PVS e o comprimento do trecho. Deve ser maior ou igual a declividade mínima.
- Diâmetro: Diâmetro nominal do trecho. Deve ser maior ou igual ao trecho de montante.
- Capacidade de vazão para lâmina adotada: Vazão máxima que o trecho suporta considerando a lâmina máxima definida nos dados de entrada e estabelecida por norma.
$$
Q_{max} = \frac{1}{n} A R_h^{2/3} I_0^{1/2} \tag{23}
$$
Fixando-se a lâmina máxima, pode-se calcular por meio da hidráulica básica o ângulo central do tirante, o raio hidráulico da seção, por consequência o perímetro molhado e a área molhada.
A partir desses valores, calcula-se a capacidade de vazão pela equação de Manning. O processo de cálculo de sarjetas é o mesmo que o do cálculo de Galerias de Águas Pluviais – Um canal Aberto.
5.4.3.1 – Cálculo Hidráulico da Vazão
- Verificação do diâmetro adotado quanto a vazão: Se o deflúvio total no trecho for maior que a capacidade de vazão, será feito o redimensionamento do diâmetro, adotando primeiramente o diâmetro comercial superior mais próximo. Se não, o diâmetro incialmente adotado está verificado. Cabe lembrar que existem mais algumas verificações e que esse diâmetro escolhido pode-se alterar em função da velocidade máxima e mínima.
- Parâmetro C2: Serve de base para a determinação da lâmina líquida ou enchimento. É calculado em função do fator de condução K.
$$
K = \frac{Q}{\sqrt{S}} \tag{24}
$$
Q: Vazão total a escoar em [m³/s]
S: declividade da galeria em m/m
$$
C_2 = \frac{K}{\frac{D^{8/3}}{n}} \tag{25}
$$
Em tabela adaptada fornecida pelo DNIT, encontra-se o valor da lâmina liquida
| Y/D | C1 | C2 | C3 |
| 0,15 | 0,0739 | 0,0152 | 0,0237 |
| 0,16 | 0,0811 | 0,0174 | 0,0269 |
| 0,17 | 0,0805 | 0,0197 | 0,0304 |
| 0,18 | 0,0961 | 0,0221 | 0,034 |
| 0,19 | 0,103 | 0,0246 | 0,0377 |
| 0,2 | 0,111 | 0,0273 | 0,0418 |
| 0,21 | 0,1199 | 0,0302 | 0,0461 |
| 0,22 | 0,1261 | 0,0331 | 0,0304 |
| 0,23 | 0,1366 | 0,0361 | 0,0549 |
| 0,24 | 0,1449 | 0,0394 | 0,0597 |
| 0,25 | 0,1535 | 0,0427 | 0,0646 |
| 0,26 | 0,1623 | 0,0432 | 0,0698 |
| 0,27 | 0,1711 | 0,0498 | 0,0752 |
| 0,28 | 0,18 | 0,0535 | 0,0805 |
| 0,29 | 0,189 | 0,0573 | 0,0862 |
| 0,3 | 0,1982 | 0,0613 | 0,0921 |
| 0,31 | 0,2074 | 0,0653 | 0,0981 |
| 0,32 | 0,2167 | 0,0694 | 0,1044 |
| 0,33 | 0,226 | 0,0735 | 0,1107 |
| 0,34 | 0,2355 | 0,0777 | 0,1174 |
| 0,35 | 0,245 | 0,0818 | 0,1242 |
| 0,36 | 0,2546 | 0,0864 | 0,1312 |
| 0,37 | 0,2642 | 0,091 | 0,1383 |
| 0,38 | 0,2739 | 0,0955 | 0,1455 |
| 0,39 | 0,2836 | 0,1002 | 0,153 |
| 0,4 | 0,2934 | 0,105 | 0,1604 |
| 0,41 | 0,3032 | 0,209 | 0,1683 |
| 0,42 | 0,313 | 0,1148 | 0,1762 |
| 0,43 | 0,3229 | 0,1198 | 0,1844 |
| 0,44 | 0,3328 | 0,1248 | 0,1926 |
| 0,45 | 0,342 | 0,1298 | 0,2014 |
| 0,46 | 0,3527 | 0,1347 | 0,2098 |
| 0,47 | 0,3627 | 0,1401 | 0,2185 |
| 0,48 | 0,3727 | 0,1451 | 0,2276 |
| 0,49 | 0,3827 | 0,1508 | 0,2368 |
| 0,5 | 0,393 | 0,1559 | 0,2464 |
| 0,51 | 0,403 | 0,1612 | 0,255 |
| 0,52 | 0,413 | 0,1668 | 0,2651 |
| 0,53 | 0,423 | 0,1719 | 0,2751 |
| 0,54 | 0,433 | 0,1773 | 0,2853 |
| 0,55 | 0,443 | 0,1828 | 0,2956 |
| 0,56 | 0,453 | 0,1883 | 0,3069 |
| 0,57 | 0,462 | 0,183 | 0,3157 |
| 0,58 | 0,472 | 0,1988 | 0,3263 |
| 0,59 | 0,482 | 0,2038 | 0,3374 |
| 0,6 | 0,492 | 0,2098 | 0,3466 |
| 0,6 | 0,492 | 0,2098 | 0,3466 |
| 0,62 | 0,512 | 0,2202 | 0,3717 |
| 0,63 | 0,522 | 0,2251 | 0,3828 |
| 0,64 | 0,5310. | 0,2305 | 0,3949 |
| 0,65 | 0,54 | 0,2354 | 0,4062 |
| 0,66 | 0,55 | 0,241 | 0,4162 |
| 0,67 | 0,559 | 0,2461 | 0,4312 |
| 0,68 | 0,569 | 0,251 | 0,4444 |
| 0,69 | 0,578 | 0,2561 | 0,457 |
| 0,7 | 0,587 | 0,2607 | 0,47 |
| 0,71 | 0,696 | 0,2659 | 0,4831 |
| 0,72 | 0,605 | 0,2705 | 0,4987 |
| 0,73 | 0,614 | 0,2751 | 0,5108 |
| 0,74 | 0,623 | 0,2798 | 0,524 |
| 0,75 | 0,632 | 0,2845 | 0,54 |
| 0,76 | 0,64 | 0,2881 | 0,5543 |
| 0,77 | 0,649 | 0,2928 | 0,5599 |
| 0,78 | 0,657 | 0,297 | 0,6051 |
| 0,79 | 0,666 | 0,3011 | 0,602 |
| 0,8 | 0,674 | 0,3047 | 0,6185 |
| 0,81 | 0,681 | 0,3079 | 0,6348 |
| 0,82 | 0,689 | 0,3115 | 0,6526 |
| 0,83 | 0,697 | 0,3151 | 0,6714 |
| 0,84 | 0,704 | 0,3183 | 0,6898 |
| 0,85 | 0,712 | 0,3212 | 0,7106 |
| 0,86 | 0,719 | 0,3243 | 0,727 |
| 0,87 | 0,725 | 0,3263 | 0,7527 |
| 0,88 | 0,732 | 0,3267 | 0,7767 |
| 0,89 | 0,738 | 0,33 | 0,8017 |
- Tirante normal: O tirante normal é a lâmina d’água no trecho de galeria. É obtido por métodos iterativos ou por tabelas. Serve de base para o cálculo dos níveis d’água nos poços e trechos de galeria. Além disso, tem grande função na caracterização do escoamento, sendo no projeto de galerias calculado de modo que sempre seja menor que o tirante crítico, garantindo a fluvialidade do canal de galeria dimensionado.
- Tirante crítico: Valor da altura de água relativa ao escoamento crítico da galeria. O tirante crítico poderá ser determinado pelo cálculo do módulo crítico
$$
M = \frac{Q}{\sqrt{g}} \tag{26}
$$
O valor do módulo crítico é utilizado para o cálculo do parâmetro , de acordo com a seguinte equação:
$$
c_3 = \frac{M}{D^{5/2}} \tag{27}
$$
5.4.3.1 – Classificação do Escoamento
- Velocidade de escoamento: Obtida pela razão entre a vazão total a escoar e a área.
A partir da comparação entre o valor do tirante normal e o valor do tirante crítico, classifica-se o escoamento em:
$y_c > y~\rightarrow~$Regime supercrítico torrencial
$y_c = y~\rightarrow~$Regime crítico
$y_c < y~\rightarrow~$Regime sub-crítico fluvial
A área é obtida pelo produto do diâmetro com o tirante normal, já calculado.
-
- Verificação da velocidade de escoamento: A velocidade de escoamento deve estar situada entre a máxima e a mínima.
- Extensão: Comprimento medido em planta no traçado da rede
- Tempo de percurso: Obtido pela razão entre o comprimento entre PVs e a velocidade.
$$
t_p = \frac{L}{60.v} \tag{28}
$$
L: [m]
v: [m/s]
5.4.4 – ABA Sarjetas

5.4.4.1 – Geometria da Rua
-
-
- Largura da via: Largura da via medida no sentido transversal ao eixo da via.
- Altura da guia: Valor da altura do meio-fio, retirado do plano diretor do município.
- Distância máxima entre bocas de lobo: Demonstrado anteriormente, a distância máxima entre bocas de lobo é dada pela seguinte equação:
-
5.4.4.2 – Dados da Sarjeta
Altura da lâmina adotada: Valor da lâmina d’água admitida no projeto da sarjeta
Largura da sarjeta: Valor estabelecido de acordo com a norma vigente do município. Pode ser alterado em função da necessidade de se alocar menos ou mais bueiros. Além disso este valor deve ser tal que uma pessoa normal consiga atravessa-la com apenas um passo.
Z: Tangente do ângulo entre a guia e a largura da sarjeta.
$$
\Delta x = \frac{2.Q}{C.i.L_r} \tag{29}
$$
Q: [m³/s]
C: Coeficiente de runoff modificado
$L_r$: Largura da rua [m]
5.4.4.3 – Ligação das Sarjetas
Caso a ligação dos lotes seja feita na sarjeta, a sarjeta deve ter capacidade hidráulica para resistir tanto a vazão proveniente do greide, quanto da bacia de montante. Nesse caso, a estimativa da distância entre bocas de lobo é dada por:
$$
\Delta x = \frac{Q}{\frac{C_s.L_r}{2} + \frac{Q_{esc}}{L}} \tag{30}
$$
Onde Q é a capacidade da sarjeta em função da geometria, lâmina de projeto e rugosidade, Cs é o coeficiente de escoamento superfiical da via e $Q_esc$ é a vazão que escoa da bacia de montante para a sarjeta. Assume-se que a vazão que escoa para a sarjeta é proporcional à distância entre sarjetas.
5.4.4.4 – Velocidade do Escoamento em Sarjetas
Verificação quanto a máxima e a mínima velocidade: Se a velocidade da sarjeta for inferior a mínima ou superior a máxima, redimensionar a sarjeta.
Verificação do trecho: Se alguma das verificações do trecho falhar, o trecho não está verificado, se não o trecho está verificado
-
- Velocidade de escoamento: A velocidade de escoamento é determinada pela relação de Izzard.
$$
V = 0,958(Z^{-1/4}.S^{1/2}.Q^{1/4}) \tag{31}
$$
Z: Inclinação da sarjeta [m/m]
S: Declividade da rua [m/]
Q: Vazão a escoar pela sarjeta [m³/s]
6.0 – Conclusões
Uma vez elaborado um sistema de equações que resolva dinamicamente as equações de continuidade e momento em galerias de águas pluvias, nós podemos automatizar e otimizar o projeto de galerias e sarjetas pluviais.
Nossa planilha nesse vídeo abaixo mostra como podemos dimensionar um sistema de drenagem em 5 minutos, confira
Caso queira uma ferramenta 100% automática que faz todos os cálculos mencionados anteriormente entregando tanto perfis longitudinais quanto memoriais de cálculo, adquira já nossa ferramenta!
Dimensionamento de galerias de águas pluviais, sarjetas e bocas de lobo – Microdrenagem Completa

Mestre e Doutor em Engenharia Hidráulica e Saneamento pela USP – São Carlos. Pesquisador de Pós-Doutorado na University of Arizona, USA. Aluno de Doutorado na University of Texas at San Antonio, USA e Engenheiro Civil pela Universidade Estadual de Maringá. Fundou o canal Engenheiro Planilheiro em 2017 após perceber que suas planilhas poderiam dar uma contribuição real para diversos engenheiros, arquitetos e profissionais da área.


8 respostas
GOSTARIA DE COMPRAR
Olá FELINESIO. Já retomamos o estoque dela. Pode fazer a compra normalmente. Às vezes acabam as planilhas e daí precisamos repor o estoque. De qualquer forma, pode comprar agora, sem problemas!
Abraços,
Marcus.
Olá Marcus
Gostaria de saber o custo e como se dá o suporte técnico da planilha.
Ola! Eu me deixo 100% a disposicao para tirar duvidas da planilha pelo whatsapp.
Boa noite, com essa planilha consigo fazer cálculo com aduelas?
A planilha apenas faz cálculos de trechos? Não faz cálculo da rede completa?
Tenho interesse em adquirir.
Gostaria de adquirir esta planilha. Excelente trabalho, uma joia rara.
Como faço para adquir esta planilha de drenagem urbana e mais a da hidráulica?