Modelo de Streeter-Phelps – Autodepuração de Rios
Princípio Físico-Biológico – Autodepuração
A ideia básica desse modelo é que existem dois fenômenos conflitantes na geração e no consumo de oxigênio dissolvido e de DBO.
Primeiro, os microrganismos presentes na água precisam de oxigênio dissolvido para consumir a matéria orgânica.
Assim, quanto maior o oxigênio dissolvido, maior a taxa de consumo de micro-organismos e, portanto, maior vai ser a redução da DBO.
Isso implica que, se introduzirmos mais oxigênio na água, haverá maior oportunidade de reduzir a carga de DBO, pois haverá menos competição por OD.
Num cenário oposto à ausência de OD e à alta carga de DBO (e.g., eutrofização), a competição elevada pelo OD faz com que sua taxa decaia rapidamente, eventualmente chegando inclusive a valores negativos.
Nesses casos, o modelo de Streeter-Phelps já não funciona.
Modelo Diferencial
A equação da continuidade molar é geralmente usada para expressar a taxa de variação da concentração de uma determinada informação ao longo do espaço, nas dimensões x, y, z, de modo que:
$$
\frac{\partial(C u)}{\partial x}+\frac{\partial(C v)}{\partial y}+\frac{\partial(C w)}{\partial z}-r=-\frac{d C}{d t} \tag{1}
$$
Onde $u$, $v$, e $w$ são as velocidades nos eixos $x$, $y$ e $z$. A variável $r$ é a taxa de reação ou taxa de geração da informação e tipicamente é assumida como uma reação de primeira ordem.
Dessa maneira, podemos aplicar a equação anterior tanto para oxigênio dissolvido $OD$ quanto para a $DBO$ última ($L$), resultando em:
$$
\frac{\partial(O D \cdot u)}{\partial x}+\frac{\partial(O D \cdot v)}{\partial y}+\frac{\partial(O D \cdot w)}{\partial z}-r_{O D}=-\frac{d O D}{d t} \tag{2} \label{equ:OD1}
$$
$$
\frac{\partial(L u)}{\partial x}+\frac{\partial(L v)}{\partial y}+\frac{\partial(L w)}{\partial z}-r_L=-\frac{d L}{d t} \tag{3} \label{equ:OD2}
$$
Finalmente, assumindo taxas de reação de primeira ordem tanto para $L$ quanto para $OD$, temos que:
$$
r_L=-k_1 L \tag{4}
$$
$$
r_{O D}=k_2\left(C_S-C_{O_2}\right) – k_1 L \tag{5}
$$
Onde $C_s$ é a concentração de saturação de oxigênio, que depende tanto da altitude quanto da temperatura.
Abaixo temos uma tabela tirada do Von Sperling que relaciona essa variável com a altitude e a temperatura.
$$
\begin{aligned}
&\text { Concentração de Saturação (mg/L) }\\
&\begin{array}{ccccc}
\hline \text { Temperatura } & \text { Altitude }(\mathrm{m}) & & & \\
& 0 & 500 & 1000 & 1500 \\
\hline 10 & 11.3 & 10.7 & 10.1 & 9.5 \\
11 & 11.1 & 10.5 & 9.9 & 9.3 \\
12 & 10.8 & 10.2 & 9.7 & 9.1 \\
13 & 10.6 & 10 & 9.5 & 8.9 \\
14 & 10.4 & 9.8 & 9.3 & 8.7 \\
15 & 10.2 & 9.7 & 9.1 & 8.6 \\
16 & 10 & 9.5 & 8.9 & 8.4 \\
17 & 9.7 & 9.2 & 8.7 & 8.2 \\
18 & 9.5 & 9 & 8.5 & 8 \\
19 & 9.4 & 8.9 & 8.4 & 7.9 \\
20 & 9.2 & 8.7 & 8.2 & 7.7 \\
21 & 9 & 8.5 & 8 & 7.6 \\
22 & 8.8 & 8.3 & 7.9 & 7.4 \\
23 & 8.7 & 8.2 & 7.8 & 7.3 \\
24 & 8.5 & 8.1 & 7.6 & 7.2 \\
25 & 8.4 & 8 & 7.5 & 7.1 \\
26 & 8.2 & 7.8 & 7.3 & 6.9 \\
27 & 8.1 & 7.7 & 7.2 & 6.8 \\
28 & 7.9 & 7.5 & 7.1 & 6.6 \\
29 & 7.8 & 7.4 & 7 & 6.6 \\
30 & 7.6 & 7.2 & 6.8 & 6.4 \\
\hline
\end{array}
\end{aligned}
$$
A solução da continuidade molar nas 3 dimensões pode ser excessivamente complexa e, no caso de rios, geralmente não é utilizada.
De fato, em rios onde o escoamento 2-D ou 3-D é dominante, modelos mais completos deveriam ser utilizados.
No entanto, rios são um exemplo em que soluções 1-D são razoáveis e esse será o foco desse texto daqui para frente.
Solução Analítica – Caso 1-D Permanente:
Autodepuração
O caso de regime permanente assume que a velocidade permanece constante ao longo de todos os subtrechos do rio.
Imagine que temos um rio de comprimento $L$ e o dividimos em intervalos discretos de tamanho $\Delta x$
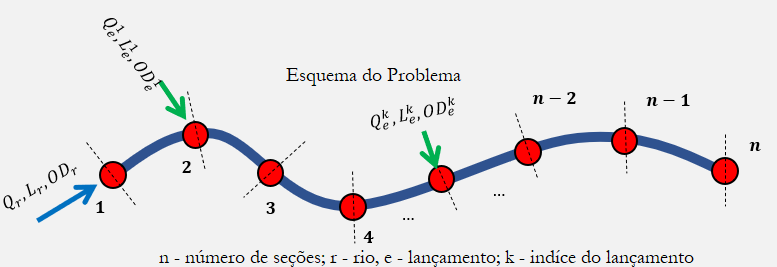
Onde $Q_r$, $L_r$, $OD_r$ são as propriedades de entrada do rio e $Q_e$, $L_e$, $OD_e$ são as propriedades do lançamento de efluente.
Vamos desprezar nessa etapa o lançamento de efluentes ao longo dos trechos, de modo que apenas o lançamento na entrada da seção 1 é considerado no cálculo da autodepuração.
Desse modo, temos $N_x = L \Delta x + 1$, onde $N_x$ é o número de nós ou seções de rio.
Vamos resolver as equações para cada um desses pontos no espaço e no tempo.
Porém, como o regime é permanente, o tempo é uma combinação linear do espaço, de modo que $t = u.x$, onde $x$ é a coordenada da seção.
Assim, resolver para $t$ ou para $x$ é equivalente, isto é, basta substituirmos $t = x.u$ nas equações de Steeter-Phelps.
O primeiro passo é simplificar as Eqs. \eqref{equ:OD1} e \eqref{equ:OD2} para o caso 1-D ao longo de $x$, resultando em:
\frac{\partial L}{\partial x}=-\frac{k_1}{u} L \tag{6}
$$
Essa equação tem solução analítica dada por:
$$
L(x)=L(0) e^{-\frac{k_1}{x} x} \tag{7} \label{equ:L0}
$$
Onde $L_0$ é a $DBO$ última no ponto inicial.
Assim, dada a concentração de $DBO$ da mistura no ponto inicial, basta resolver Eq. \eqref{equ:L0} para cada $x$.
Agora, precisamos resolver a equação do oxigênio dissolvido, que tem a seguinte solução
$$
D(x)=D_0 e^{-\frac{k_2}{u} x}+\frac{k_1 L_0}{k_2-k_1}\left[e^{-\frac{k_1}{u} x}-e^{-\frac{k_2}{u} x}\right] \tag{8}
$$
Onde $D(x) = C_s – OD(x)$.
Perceba que essas equações são válidas apenas para um único lançamento e que o eixo $x$ é orientado a partir do ponto de lançamento.
Em casos com mais lançamentos, precisamos alterar o sistema de referências. Isso é fundamental para o uso adequado das equações em casos de vários lançamentos.
Exemplo 1)
Qual a DBO última e a concentração de oxigênio dissolvido a $300~km$ de um rio que tem concentrações de $OD$, $DBO_5$ e Vazão de 7 $mg/L$, 10 $mg/L$ e 0.5 $m^3/s$.
Além disso, utilize um intervalo de discretização de 1000 m.
Esse rio sofre um lançamento pontual na entrada da seção com $OD$, $DBO_5$ e vazão de 0 $mg/L$, 300 $mg/L$ e 0.1 $m^3/s$.
A temperatura do rio e sua altitude média são de $25~C^{\circ}$ e $1000~m$, respectivamente, resultando em $C_s = 7.5~mg/L$.
Assuma também $K_1 = 0.48/dia$ e $K_2 = 4/dia$, ambos a $20~C^{\circ}$.
Solução:
Antes de resolvermos as equações analíticas do modelo de Streeter-Phelps, precisamos primeiro corrigir $K_1$ e $K_2$ para a temperatura de $25~C^{\circ}$. Desse modo, corrigimos ambos com:
$$
\begin{aligned}
& K_{1, T}=K_{1,20} \theta_1^{T-20} \\
& K_{2, T}=K_{2,20} \theta_2^{T-20}
\end{aligned}
$$
Onde $\theta_1 = 1.047$ e $\theta_2 = 1.024$, resultando em $K_{1,25} = 0.60$ e $K_{2,25} = 4.5$.
Agora, precisamos calcular as concentrações da mistura. Essa etapa consiste em calcular médias ponderadas em função da vazão.
Assim, a vazão total $Q_{tot} = 0.5 + 0.1 = 0.6~m^3/s$, $L_{5,mix} = 58.33~mg/L$ e $OD_{mix} = 5.83~mg/L$.
No entanto, precisamos corrigir entre o valor da $DBO_5$ para a $DBO_u$, fazendo:
$$
K_T=\frac{1}{1-\exp \left(-5 K_1\right)}=\frac{L_0}{L_{5, \text { mix }}}=\frac{D B O_5}{D B O_u} \Rightarrow L_0=L_{5, \text { mix }} K_T \tag{9}
$$
O que implica que $L_{5,mix} = 61.39~mg/L = L_u(0)$.
Agora, basta resolvermos a equação do oxigênio dissolvido para diversos valores de x, o que resulta nos gráficos abaixo.
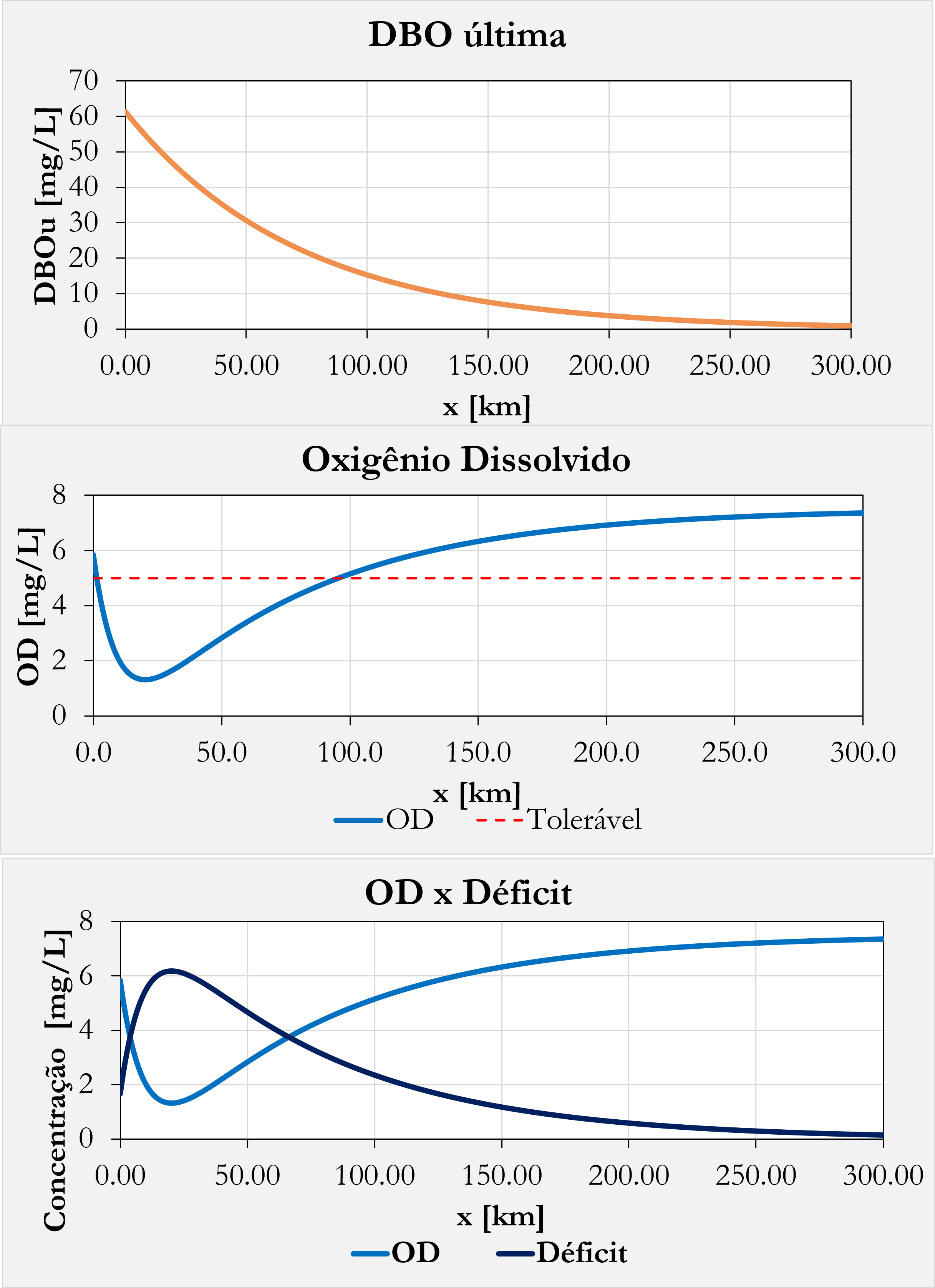
Portanto, o $OD$ e a $L_u$ em 300 km são de $7.35~mg/L$ e $0.96~mg/L$. Já o valor mínimo de OD foi de 1.35 mg/L e ocorreu à 1.35 km do lançamento.
Solução Numérica – Caso 1-D Quasi-Permanente
Um dos maiores problemas encontrados nas modelagens simples, como mostradas anteriormente, é assumir que apenas 1 lançamento irá ocorrer no cálculo de autodepuração de rios.
Na verdade, as equações de Streeter-Phelps só são válidas no caso homogêneo de lançamento único.
Na prática, isso pode não acontecer, especialmente em rios maiores com vários lançamentos.
Desse modo, precisamos resolver as equações numericamente, em vez de analiticamente.
Em outras palavras, ao invés de resolver a equação no domínio do tempo, resolvemos elas no domínio do espaço, discretizando-a no espaço.
Para isso, vamos imaginar há vários $n$ lançamentos em posições conhecidas $\mathbf x_{ref}$ tal que $\mathbf x_l = [x_{ref,1}, x_{ref,2}, \dots x_{ref,n}]^\mathrm T$.
No entanto, como mencionado anteriormente, as equações de Streeter-Phelps só são válidas para trechos homogêneos com 1 lançamento e com o eixo x local orientado a partir da coordenada desse lançamento.
Assim, vamos definir essa coordenada relativa $x_*^i = x – x_{ref,i}$ para todos os lançamentos de $i = 1$ a $ i = n$.
Além disso, caso as velocidades mudem (i.e., vão mudar se o regime for quasi-permanente), $K_2$, pode ser calculado pelos métodos de O’CONNOR e DOBBINS, OWENS et al. e CHURCHILL et al.
Finalmente, podemos escrever uma equação que vale para cada coordenada x mas que leva em conta os eixos locais de cada lançamento, de modo que:
$$
D_t\left(x^*\right)=\frac{K_1 L_0\left(x_{r e f}\right)}{K_2-K_1}\left[\exp \left(-K_1 \frac{x^*}{u}\right)-\exp \left(-K_2 \frac{x^*}{u}\right)\right]+D_0\left(x_{r e f}\right) \exp \left(-K_2 \frac{x^*}{u}\right) \tag{10}
$$
De maneira semelhante, a concentração de DBO última também será calculada da seguinte forma:
L\left(x^*\right)=L_0\left(x_{r e f}\right) \cdot \exp \left(-K_1\left(\frac{x^*}{u}\right)\right) \tag{11}
$$
Exemplo 2)
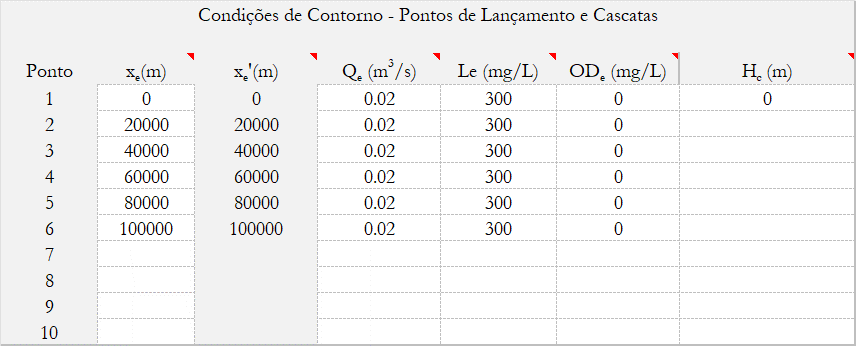
O mesmo rio do exemplo anterior agora recebe 5 lançamentos de 20 L/s, 300 mg/L de DBO e 0 mg/L de ODe a cada 20 km. Determine o perfil de OD e de DBO ao longo do rio.
Assuma $x_f$ = 300 km e intervalos de 0.5 km.
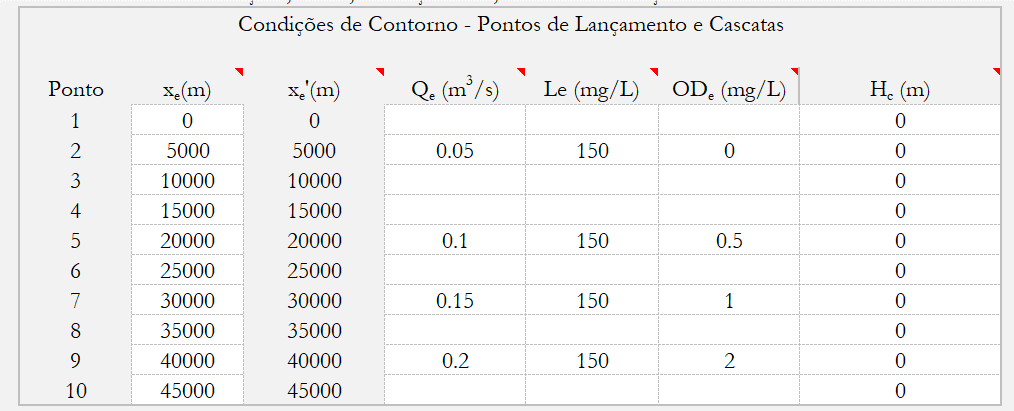
Onde $Q_e$ é a vazão de lançamento, $L_e$ a $DBO_5$, $OD_e$ a concentração de $OD$ no lançamento.
Assuma também que o rio tem uma seção transversal aproximadamente retangular, com largura e altura constantes de 2 m e 0,5 m, respectivamente, sendo a velocidade variável ao longo do comprimento.
Assim, dada uma vazão $Q$ conhecida, a velocidade pode ser calculada como $u = Q/(b.h)$.
Resultados
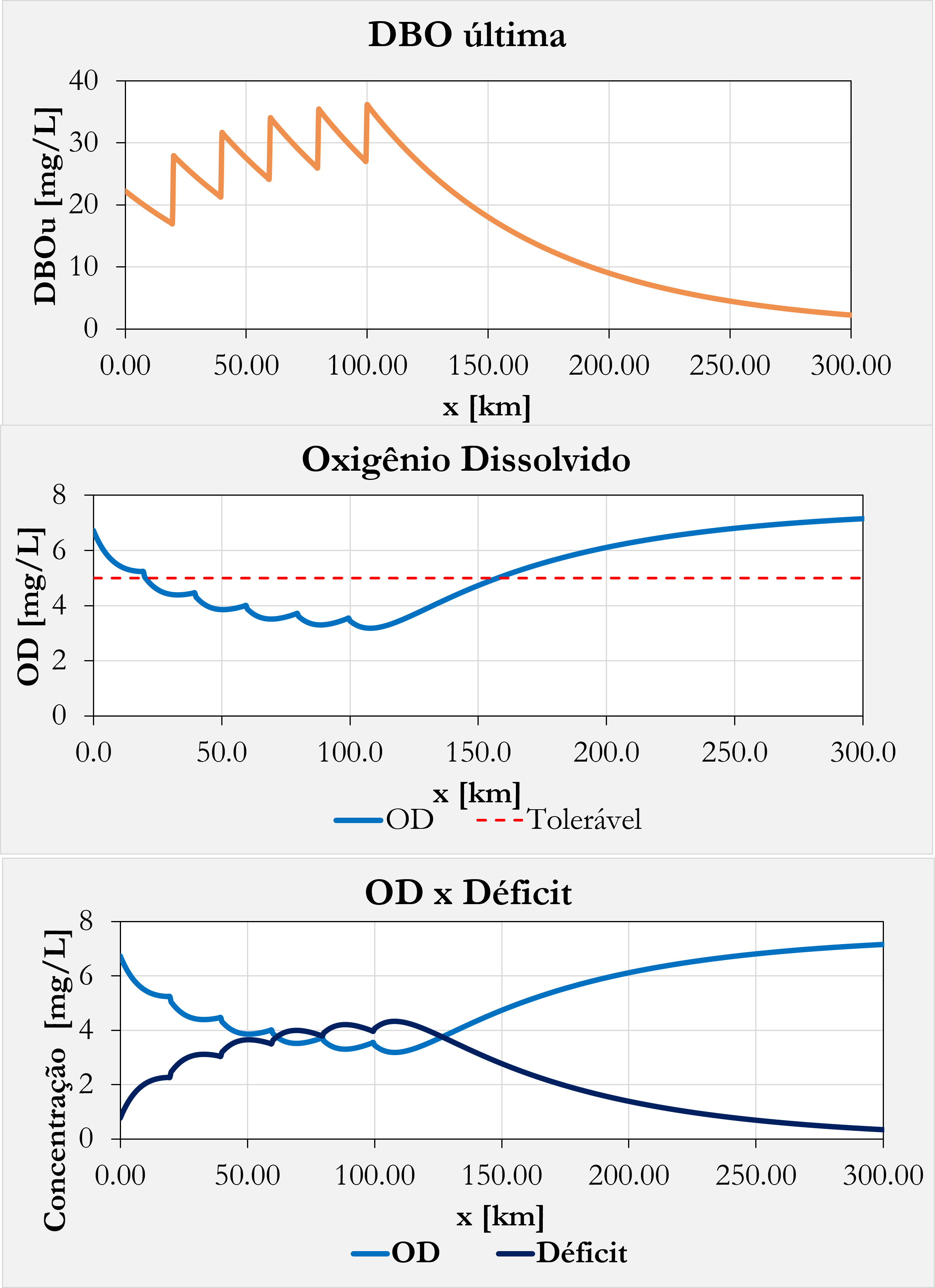
Perceba que o rio sofreu excessivamente com os lançamentos e não é capaz de estabelecer valores aceitáveis de OD ao longo de grande parte de seu comprimento.
Precisamos propor alguma solução.
Por isso, a planilha pode ser uma ferramenta útil para avaliar novas soluções para atender aos requisitos de qualidade da água.
Planilha Excel – Autodepuração por Streeter-Phelps
Na planilha, você pode testar soluções colocando cascatas, alterando os valores de $K_1$, testando diversos pontos de lançamento, variando o valor de $K_2$ para cada trecho e muito mais!
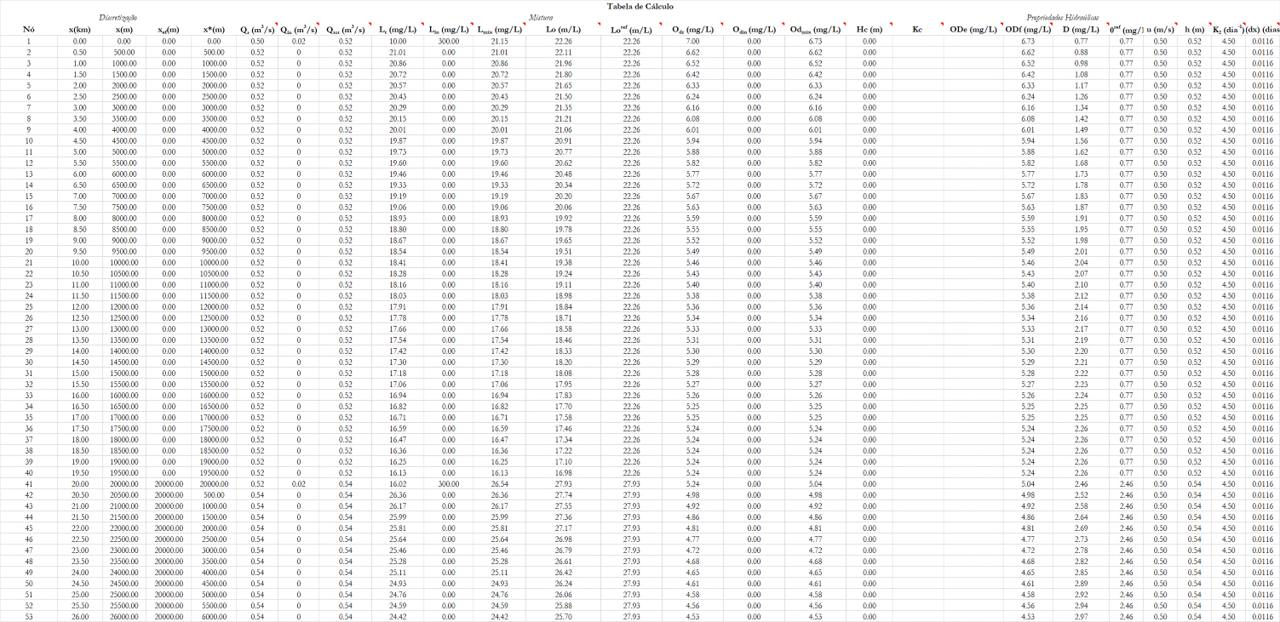
Quer fazer cálculos de autodepuração em rios em 5 minutos e garantir projetos seguros, eficientes e dentro das normas?
Adquira já a planilha!
Parcelamos em até 12x sem juros!
Entre em contato direto comigo clicando aqui que vou lhe passar todas informações, tirar suas dúvidas e te anteder pessoalmente.
Ou entre em contato pelo whatsapp do meu site que minha equipe também vai lhe atender o mais rápido possível.
Espero que esse texto lhe seja útil!
Um grande abraço,
Marcus.

Mestre e Doutor em Engenharia Hidráulica e Saneamento pela USP – São Carlos. Vencedor do Prêmio Tese Destaque de teses da USP (2024) e autor de diversos artigos nacionais e artigos internacionais. Pesquisador de Pós-Doutorado II na University of Arizona, Department of Hydrology and Atmospheric Sciences, USA. Engenheiro civil formado pela Universidade Estadual de Maringá. Fundou o canal Engenheiro Planilheiro em 2017 após perceber que suas planilhas poderiam dar uma contribuição real para diversos engenheiros, arquitetos e profissionais da área, contando com mais de 100 mil planilhas já baixadas e diversos clientes atendidos no Brasil e no mundo.



Uma resposta
Boa tarde
Gostei da planilha.
Gostaria de saber o preço da planilha.