Distribuição de Gumbel – Hidrologia Estatística
Fundamentação da Distribuição de Gumbel
A distribuição de Gumbel é usualmente aplicada a valores extremos com coeficiente de assimetria positivo.
Ela basicamente leva em conta dois dados de entrada: o desvio padrão e a média.
A distribuição Gumbel pode ser descrita pelas seguintes relações:
$$\mathrm{Prob}(x \leq x_m) = \mathrm{e}^{-\mathrm{e}^{-b}}$$
onde $b$ é um parâmetro da disrtibuição de Gumbel que vamos discutir logo adiante.
De maneira análoga a equação anterior, podemos dizer que:
$$\mathrm{Prob}(x \geq x_m) = 1 – \mathrm{Prob}(x \leq x_m)$$
onde agora expressamos a probabilidade de um evento superar ou igualar o valor de $x_m$.
O parâmetro $b$ depende das propriedades da amostra. Em particular, depende da média $\bar{x}$ e do desvio padrão $s$, e é dado como:
$$b = \frac{1}{0.7797s}(x – \bar{x} + 0.45 s) \tag{1}$$
Se usarmos a relação que:
$$ \mathrm{TR} = \frac{1}{\mathrm{Prob}(x \geq x_m)} \tag{2}$$
podemos aplicar a primeira equação e isolar a variável aleatória $x$, de modo que:
$$x = \bar{x} – s(0.45 + 0.7797 \mathrm{ln} \Bigl[\mathrm{ln}\Bigr(\frac{\mathrm{TR}}{\mathrm{TR}-1} \Bigl) \Bigr]) \tag{3}$$
Perceba que a equação anterior nos dá, para qualquer valor de $x$ (i.e., 100 mm se for chuva ou 200 $\mathrm{m^3/s}$ se for vazão, por ex), em função do tempo de retorno e da característica da amostra, isto é, seu desvio padrão e média.
Exemplo 1)
Dada a série de precipitações $\mathbf{P} = [100,~120,~200,~150,~160,~175,~155,~170,~165,~190,~175,~200]^T$, determine o valor esperado de precipitações máximas para um tempo de retorno de 10 anos.
Solução:
Calculando a média e o desvio padrão chegamos em 163.33 mm e 29.9 mm.
Agora, basta ordenar os dados e montar uma tabela em que consigamos determinar o valor de $b$ para cada valor de $x$.
Coloquemos:
Col 1 – Ordenação de 1 a 12, representando os 12 maiores valores da série.
Col 2 – Valores ordenados da variável aleatória começando do maior para o menor
Col3 – Valor de b calculado por $b = \frac{1}{0.7797s}(x – \bar{x} + 0.45 s)$
Col 4 – Valor da probablidade de excedência $\mathrm{Prob}(x \geq x_m)$
Col 5 – Tempo de retorno associado calculador por $\mathrm{TR} = \frac{1}{\mathrm{Prob}(x \geq x_m)}$.
A aplicação dessa tabela pode ser vista abaixo:
| Ordenação | P (mm) | b | $P(x>= x_m)$ | TR |
| 1 | 200 | 2.15 | 0.11 | 9.07 |
| 2 | 200 | 2.15 | 0.11 | 9.07 |
| 3 | 190 | 1.72 | 0.16 | 6.09 |
| 4 | 175 | 1.08 | 0.29 | 3.46 |
| 5 | 175 | 1.08 | 0.29 | 3.46 |
| 6 | 170 | 0.86 | 0.34 | 2.90 |
| 7 | 165 | 0.65 | 0.41 | 2.46 |
| 8 | 160 | 0.43 | 0.48 | 2.10 |
| 9 | 155 | 0.22 | 0.55 | 1.81 |
| 10 | 150 | 0.01 | 0.63 | 1.59 |
| 11 | 120 | -1.28 | 0.97 | 1.03 |
| 12 | 100 | -2.14 | 1.00 | 1.00 |
Histograma de Frequências
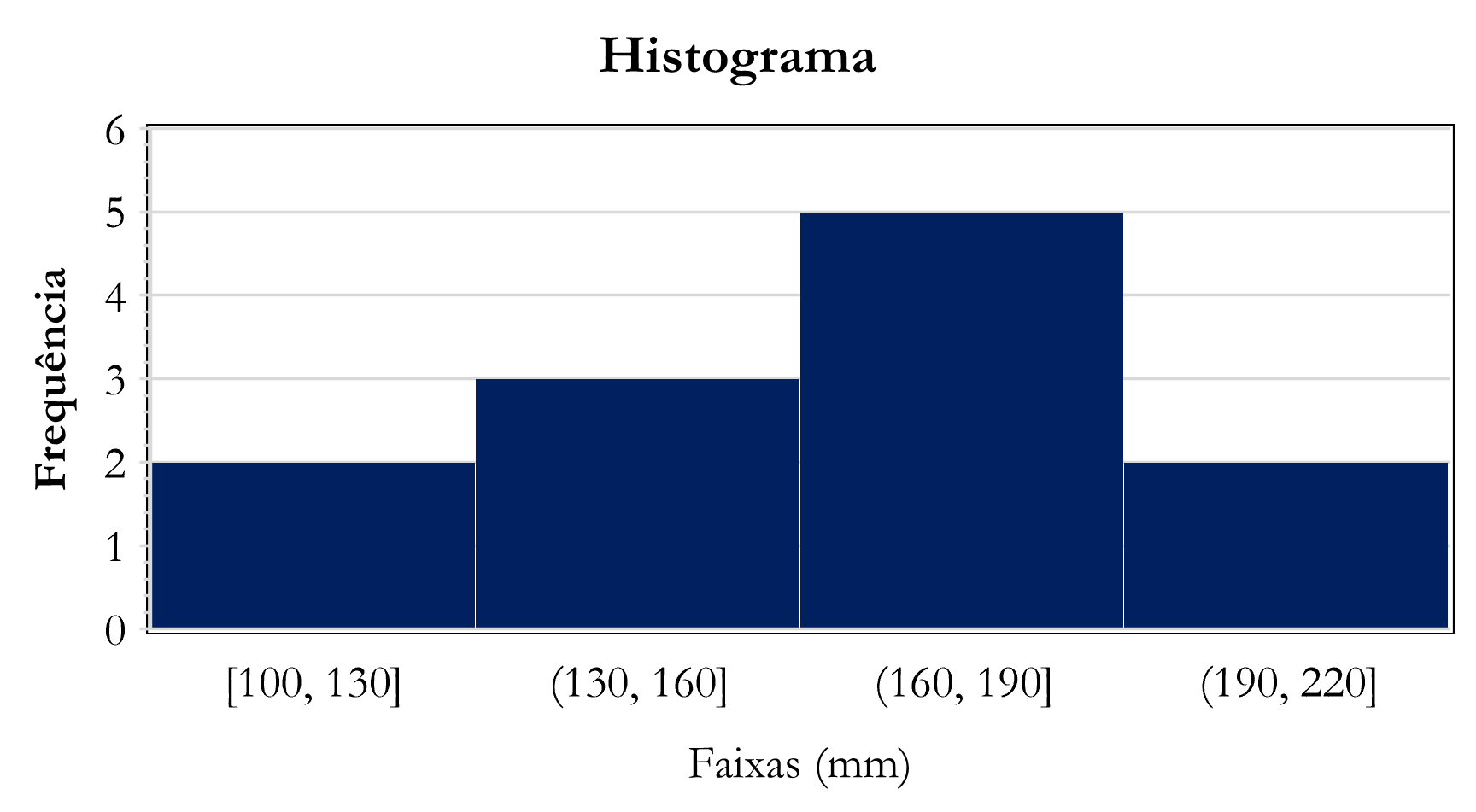
Perceba que há, aparentemente, um deslocamento da séria para valores extremos.
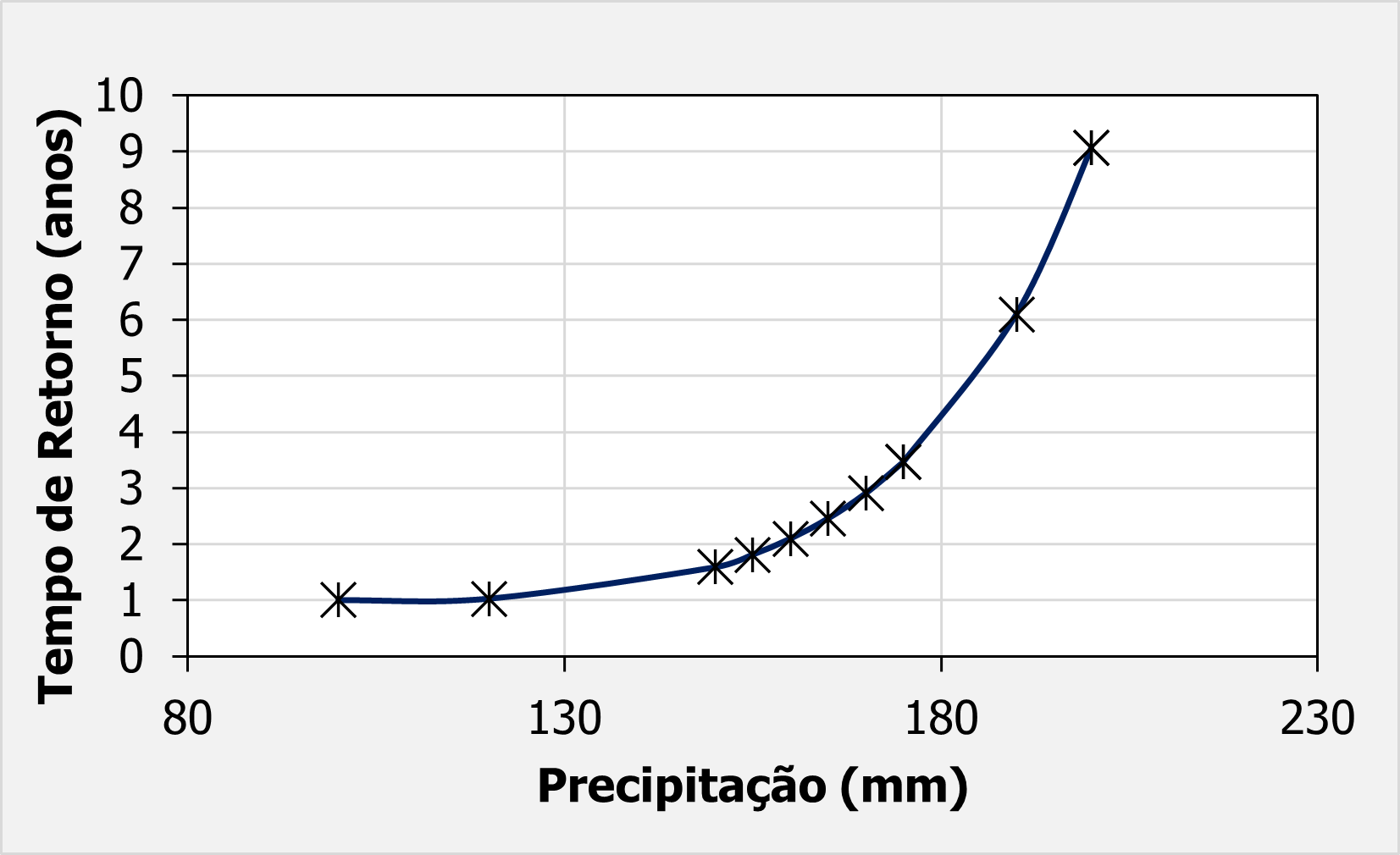
Finalmente, se formos calcular o valor da chuva para qualquer tempo de retorno, é só calcular $b$ para o valor da variável $x$, calcular a probabilidade de excedência e depois resolver $ \mathrm{TR} = \frac{1}{\mathrm{Prob}(x \geq x_m)}$.
O processo inverso também vale. Dado um tempo de retorno $\mathrm{TR}$, a probabilidade excedência, depois o valor de $b$ e por último o valor de $x$.
No caso de 10 anos, o resultado 202.4 mm
O mesmo processo vale para qualquer valor de precipitação.
Exemplo 2)
Ajuste uma distribuição de probabilidades tipo Gumbel para a seguinte série de precipitações máximas anuais, já classificadas do maior para o menor valor:
| Precipitações Máximas Anuais (mm) |
| 150.8 |
| 123.7 |
| 121.7 |
| 109 |
| 102.9 |
| 102.4 |
| 102.4 |
| 101.8 |
| 101.8 |
| 100 |
| 96.4 |
| 95.1 |
| 93.4 |
| 93.3 |
| 93 |
| 92.2 |
| 92.2 |
| 88.4 |
| 88.2 |
| 86 |
| 85.1 |
| 85 |
| 84 |
| 83.8 |
| 83.2 |
| 81.3 |
| 80.3 |
| 75.3 |
| 74 |
| 73.1 |
| 71.7 |
| 71.4 |
| 71.2 |
| 67.3 |
| 67.3 |
| 66.3 |
| 66.3 |
| 66.2 |
| 65.7 |
| 65.7 |
| 64.7 |
| 59.7 |
| 59.6 |
| 59.2 |
| 55.4 |
| 25.5 |
| 25.5 |
Para resolvermos o problema basta calcular $b$ para cada valor de precipitação observada. Para isso, primeiro precisamos calcular a média (82.309 mm) e o desvio padrão (22.5 mm) da amostra e depois calcular as probabilidades de excedência para cada valor observado.
| Cálculo para os dados observados | ||||
| Ordenação | P (mm) | b (Eq. 1) | $\mathrm{Prob}(x\leq x_m)$ (Eq. 2) | TR (Eq. 3) |
| 1 | 150.8 | 4.47 | 0.01 | 88.16 |
| 2 | 123.7 | 2.93 | 0.05 | 19.27 |
| 3 | 121.7 | 2.82 | 0.06 | 17.25 |
| 4 | 109 | 2.10 | 0.12 | 8.64 |
| 5 | 102.9 | 1.75 | 0.16 | 6.26 |
| 6 | 102.4 | 1.72 | 0.16 | 6.10 |
| 7 | 102.4 | 1.72 | 0.16 | 6.10 |
| 8 | 101.8 | 1.69 | 0.17 | 5.91 |
| 9 | 101.8 | 1.69 | 0.17 | 5.91 |
| 10 | 100 | 1.58 | 0.19 | 5.39 |
| 11 | 96.4 | 1.38 | 0.22 | 4.49 |
| 12 | 95.1 | 1.30 | 0.24 | 4.21 |
| 13 | 93.4 | 1.21 | 0.26 | 3.87 |
| 14 | 93.3 | 1.20 | 0.26 | 3.85 |
| 15 | 93 | 1.19 | 0.26 | 3.80 |
| 16 | 92.2 | 1.14 | 0.27 | 3.65 |
| 17 | 92.2 | 1.14 | 0.27 | 3.65 |
| 18 | 88.4 | 0.92 | 0.33 | 3.05 |
| 19 | 88.2 | 0.91 | 0.33 | 3.02 |
| 20 | 86 | 0.79 | 0.37 | 2.73 |
| 21 | 85.1 | 0.74 | 0.38 | 2.63 |
| 22 | 85 | 0.73 | 0.38 | 2.62 |
| 23 | 84 | 0.67 | 0.40 | 2.50 |
| 24 | 83.8 | 0.66 | 0.40 | 2.48 |
| 25 | 83.2 | 0.63 | 0.41 | 2.42 |
| 26 | 81.3 | 0.52 | 0.45 | 2.23 |
| 27 | 80.3 | 0.46 | 0.47 | 2.14 |
| 28 | 75.3 | 0.18 | 0.57 | 1.76 |
| 29 | 74 | 0.10 | 0.59 | 1.68 |
| 30 | 73.1 | 0.05 | 0.61 | 1.63 |
| 31 | 71.7 | -0.03 | 0.64 | 1.56 |
| 32 | 71.4 | -0.04 | 0.65 | 1.54 |
| 33 | 71.2 | -0.05 | 0.65 | 1.53 |
| 34 | 67.3 | -0.28 | 0.73 | 1.37 |
| 35 | 67.3 | -0.28 | 0.73 | 1.37 |
| 36 | 66.3 | -0.33 | 0.75 | 1.33 |
| 37 | 66.3 | -0.33 | 0.75 | 1.33 |
| 38 | 66.2 | -0.34 | 0.75 | 1.33 |
| 39 | 65.7 | -0.37 | 0.76 | 1.31 |
| 40 | 65.7 | -0.37 | 0.76 | 1.31 |
| 41 | 64.7 | -0.42 | 0.78 | 1.28 |
| 42 | 59.7 | -0.71 | 0.87 | 1.15 |
| 43 | 59.6 | -0.71 | 0.87 | 1.15 |
| 44 | 59.2 | -0.74 | 0.88 | 1.14 |
| 45 | 55.4 | -0.95 | 0.93 | 1.08 |
| 46 | 25.5 | -2.65 | 1.00 | 1.00 |
| 47 | 25.5 | -2.65 | 1.00 | 1.00 |
Além disso, podemos obter uma relação geral que nos fornece, para cada tempo de retorno, o valor de precipitação, de modo que:
$$P = \bar{P} – s(0.45 + 0.7797 \mathrm{ln} \Bigl[\mathrm{ln}\Bigr(\frac{\mathrm{TR}}{\mathrm{TR}-1} \Bigl) \Bigr]) $$
Aplicando os valores:
$$P(\mathrm{TR}) = 82.309 – 22.5(0.45 + 0.7797 \mathrm{ln} \Bigl[\mathrm{ln}\Bigr(\frac{\mathrm{TR}}{\mathrm{TR}-1} \Bigl) \Bigr]) $$
Conclusão
É relativamente fácil ajustar um modelo de distribuição de probabilidade de valores extremos, tipo Gumbel.
Mas a pergunta que fica é:
Como saber se o método de Gumbel se ajusta de fato a essa série de precipitações?
Vamos aprender isso nos próximos artigos na hora de fazer os Testes de Aderência.
