Modelagem de Poluentes: Build-up e Wash-off
O transporte de poluentes no escoamento superficial depende de diversos fatores, entre eles o tipo de poluente, velocidade do escoamento e características fisiográficas da bacia.
Em casos mais complexos, as equações de advecção e convecção são suficientemente adequadas para representar os processos de transporte de poluentes no escoamento superificial.
No entanto, a completa solução dessas equações requer uma descrição muito detalhada da bacia hidrográfica, isto é, dados detalhados são necessários para resolve-las.
Assim, modelos simplificados como o modelo de Build-up e Wash-off são alternativas práticas para a estimativa de concentrações e cargas de poluentes carreados no escoamento superficial.
Dinâmica do Modelo de Build-up e Wash-off
Build-up refere-se a massa de poluentes que está disponível na bacia hidrográfica.
Assim, duas fases ocorrem para o build-up.
Primeiro, durante períodos de seca, a massa de poluente na bacia tende a se acumular seguindo uma função exponencial com uma assíntota em $B_{max}$.
Segundo, durante períodos chuvosos, essa massa é varrida e lavada em direão ao exutório em função da capacidade de varrimento ou lavagem desse poluente, denominada taxa de Wash-off (exlicada adiante).
Assim, podemos escrever a dinâmica de acumulação durante períodos de seca como:
$$
B_d=C_1\left(1-\exp \left(-C_2 A D D\right)\right) \tag{1} \label{equ:buildup}
$$
Além disso, durante períodos com escoamento superficial:
$$
B(t+\Delta t)=B(t)-w(t) \Delta t+\Delta B(t) \tag{2}
$$
onde $C_1$ (kg/ha) e $C_2$ são os parâmetros do modelo de build-up, $w$ é a taxa de Wash-off e $\Delta B$ é a massa de build-up acumulada no intervalo $\Delta t$.
A taxa de Wash-off pode ser calculada como:
$$
w(t)=C_3 q^{C_4} B(t) \tag{3}
$$
onde $C_3$ e $C_4$ são os coeficientes do modelo de Wash-off e q é a vazão por unidade de área da bacia hidrográfica (mm/h).
Perceba que a taxa de lavagem é diretamente proporcional a massa disponível.
Para calcularmos a concentração de poluentes, basta dividir a taxa de lavagem pela vazão, resultando em:
$$
C(t)=w(t) / Q \tag{4}
$$
Exemplo
Determine o polutograma, a massa de sólidos suspensos totais, a carga e o diagrama de first flush que chega em um reservatório de detenção para a chuva de tempo de retorno de 1 ano e duração de 60 minutos.
Dados da Bacia
- $C_1$ = 50 kg/ha
- $C_2$ = 0.3/dia
- $C_3$ = 0.03
- $C_4$ = 1.2
- $ADD$ = 10 dias
- $t_f$ = 180 min
- $t_0$ = 0 min
- IDF: K = , a = 1519, b = 0.236 , c = 16, TR = 1 ano
- CN = 80, Área de Drenagem = 5 $km^2$.
- Chuva distribuída em Blocos Alternados
Resultados – Modelo Hidrológico
- Distribuição Temporal – Blocos Alternados
- Infiltração (SCS-CN)
- Conversão de Chuva Efetiva em Vazão – Hidrograma Unitário SCS
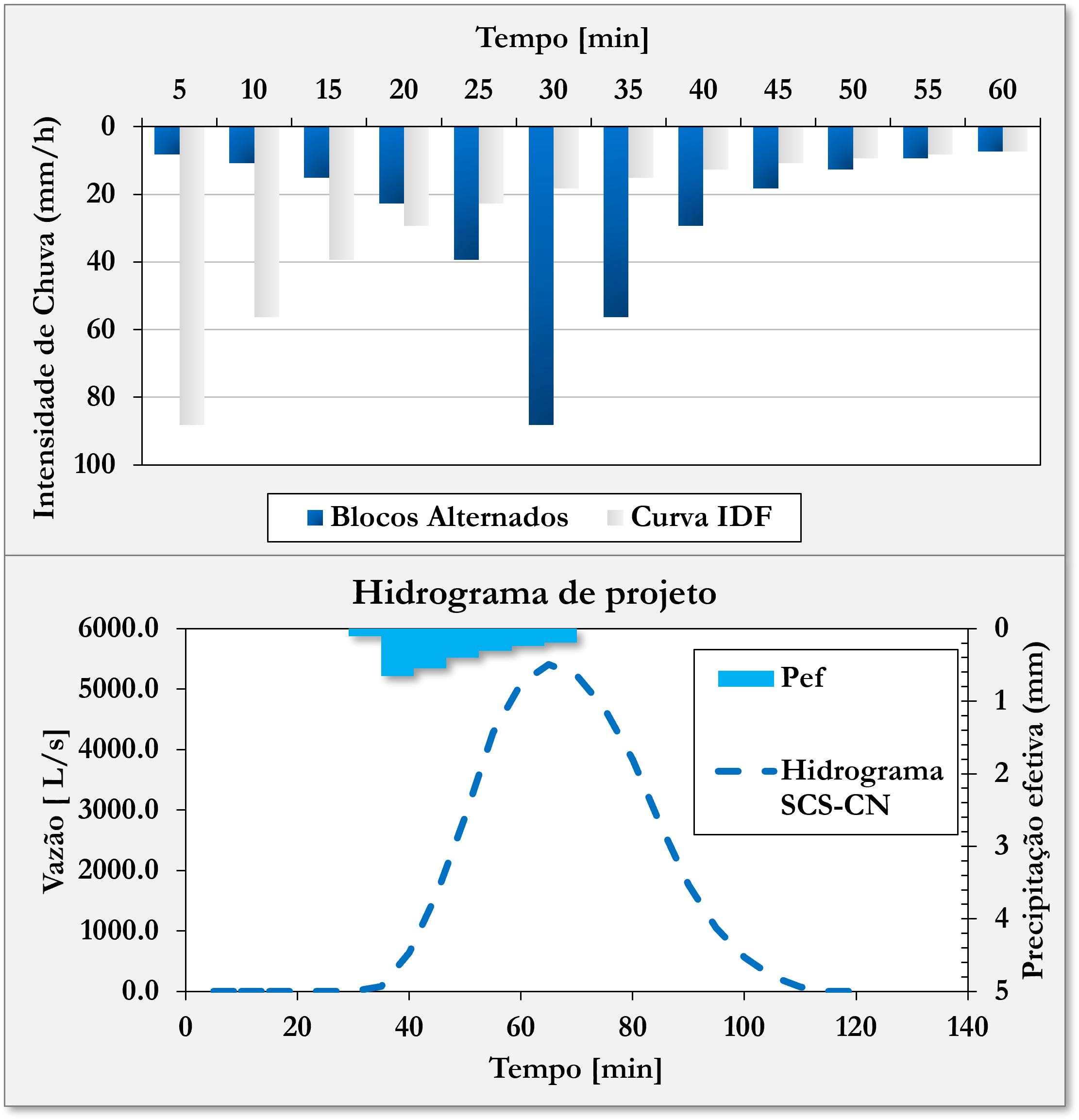
Em resumo temos:
- Vazão de Pico – 5.4 $m^3/s$
- Tempo de Pico – 65 min
- Volume de Escoamento – 0.25 $\mathrm{m^3}$ para cada 100 $\mathrm{m^2}$ de área
- Volume de Chuva – 2.65 $\mathrm{m^3}$ para cada 100$ \mathrm{m^2}$ de área
- Coeficiente de Runoff de 0.09
Agora, usamos esse hidrograma de escoamento superficial dentro do modelo de Build-up e Wash-off para estimarmos o transporte de poluentes, no caso Sólidos Suspensos Totais, durante esse evento de chuva.
Massa Inicial de Sólidos Suspensos
Nesta etapa iniciamos o processo de modelagem de poluentes.
Assim, primeiro calculamos a massa de poluentes resolvendo \eqref{equ:buildup}, resultando em $B_d = 47.51 kg/ha$, ou seja, em cada hectare de área de drenagem é esperado uma acumulação de 47 kilos de sólidos suspensos totais.
Resultados do Modelo de Build-up e Wash-off
Os resultados da simulação resolvendo as equações de wash-off mencionadas nesse artigo resultam nas seguintes figuras:
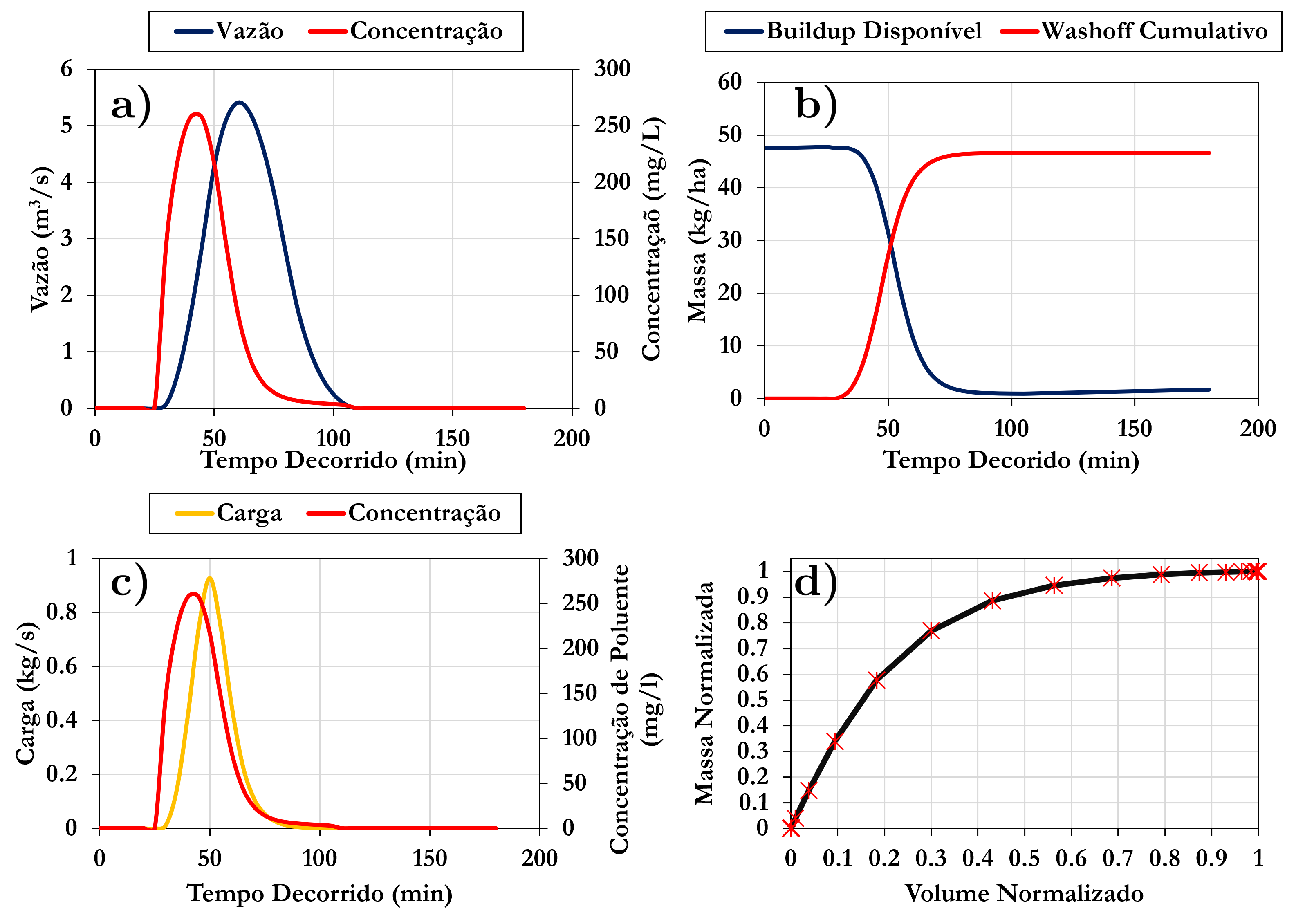
Em resumo, um evento de tempo de retorno de 1 ano, nessa bacia de 5 km2, lava 98% dos poluentes disponíveis, gerando uma concentração de pico de cerca de 250 mg/L e carga máxima de aproximadamente 0.8 kg/sec.
