Balanço Hídrico Anual

Princípios

O balanço hídrico anual é controlado pela competição entre disponibilidade hídrica e disponibilidade energética, medida pelo índice de aridez.

O clima, expressado como variável de primeira ordem pelo índice de aridez, captura mudanças de local para local, assim como os efeitos de mudanças climáticas.

Hipóteses Adotadas no Balanço Hídrico Anual

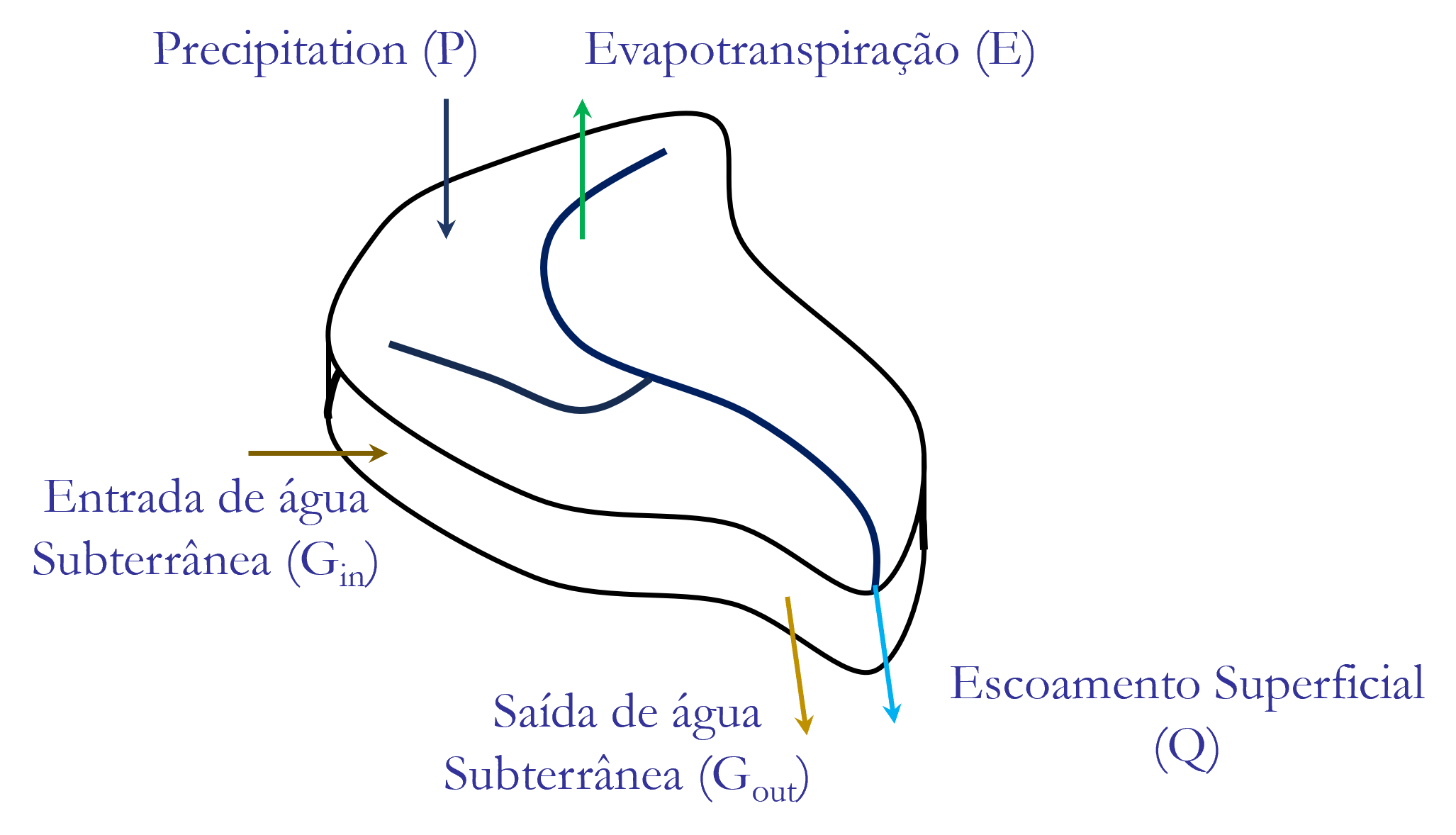
Assumindo intervalos de tempos discretos, o balanço hídrico dessa bacia pode ser descrito como:

$$
\frac{\Delta S}{\Delta t}=\bar{P}+\overline{G_{\text {in }}}-\left(\bar{E}+\bar{R}+\overline{G_{\text {out }}}\right)
$$

onde os valores com supercrito em barra representam valores médios anuais de longo termo, $\Delta t$ é um intervalo de tempo como por ex 1 ano e $S$ é o armazenamento de água interno na bacia.

Nas médias de longo termo, isto é, anos, décadas, os termos de escoamento subterrâneo tendem a se cancelar.

Além disso, a variação do volume armazenado também é considerada como nula em médias de longo termo, o que simplifica a equação anterior a:

$$ \bar{P} = \bar{Q} + \bar{E}$$

Exemplo 1 

A partir de registos hidrológicos de mais de 50 anos numa área de captação de 500 km², a precipitação média anual foi estimada em 990 mm e o escoamento médio anual em 330 mm. Um reservatório localizado logo à jusante do exutório da bacia, com uma área média de 1700 hectares (100 hectares = 1 km²), é projetado para coletar o escoamento disponível para fornecer água a uma comunidade próxima.

Além disso, a evaporação anual sobre a superfície do reservatório é estimada em 1200 mm.

Não há perdas de ou entrada de água subterrânea no reservatório.

Determine a retirada média anual disponível do reservatório para abastecimento de água em mm sob a suposição de que 90% da água que entra no reservatório será liberada para sustentar o fluxo a jusante.

Solução

Área do reservatorio = 17 km2, convertendo

Volume de escoamento superficial que chega no reservatorio = 300 mm * (500 km² / 17 km²) = 9705 mm

Volume total que chega no reservatório = Volume afluente de escoamento superficial – Evaporação + Precipitação

Volume total que chega no reservatório = 9705 – 1200 + 330 = 9495 mm

90% desse volume passa como escoamento de jusante do reservatório, ou seja, apenas 10% do volume disponível é utilizado para retirada. Assim

Volume retirado = 10% de 9495 mm = 949 mm 

Exemplo 2 

Uma bacia localizada na Geórgia, Estados Unidos, tem as seguintes observações de precipitação, evapotranspiração e vazão médias observadas:

Mês	$P$ [mm]	$E$ [mm]	$Q$ [mm]
1	135	24	58
2	131	34	62
3	155	56	79
4	122	79	72
5	114	112	55
6	103	124	39
7	121	121	34
8	115	103	30
9	93	71	28
10	90	47	32
11	99	29	37
12	125	23	50

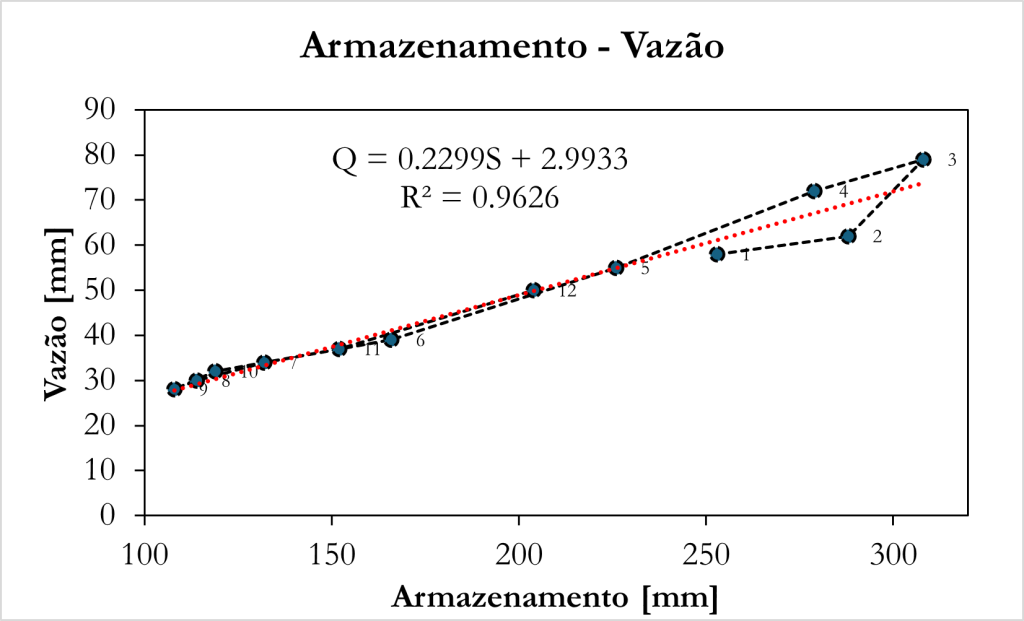
Calcule a climatologia de 1 ano e a relação entre armazenamento e vazão (storage-discharge relationship). Assuma que o armazenamento inicial, ou seja, ao final de dezembro do ano anterior, é 200 mm.

Solução:

Primeiro montamos uma coluna extra que calcule o armazenamento $S$, de modo que $S(t+\Delta t) = S(t) + \Delta P – \Delta E – \Delta Q$, todos num intervalo de 1 mes, assim como na tabela abaixo.

 

Mês	$P$	$E$	$Q$	$S(t)$	$S(t +\Delta t)$	$\Delta S$
	[mm]	[mm]	[mm]	[mm]	[mm]	[mm]
1	135	24	58	200	253	53
2	131	34	62	253	288	35
3	155	56	79	288	308	20
4	122	79	72	308	279	-29
5	114	112	55	279	226	-53
6	103	124	39	226	166	-60
7	121	121	34	166	132	-34
8	115	103	30	132	114	-18
9	93	71	28	114	108	-6
10	90	47	32	108	119	11
11	99	29	37	119	152	33
12	125	23	50	152	204	52

 

Plotando os resultados chegamos na climatologia de 1 ano.

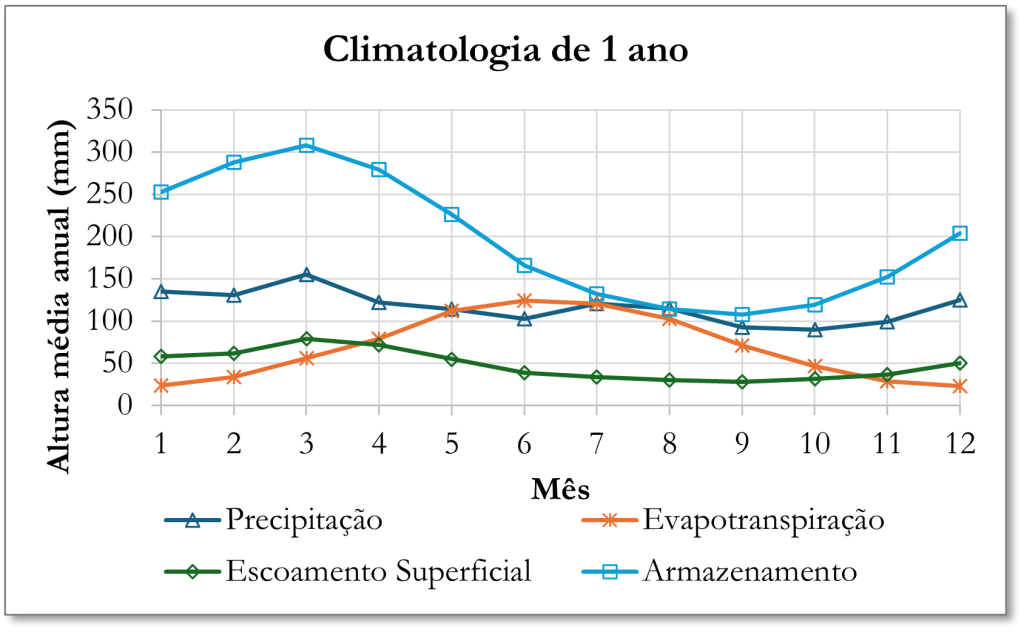
Podemos também avaliar como se da a relação entre a vazão e o armazenamento da seguinte forma:

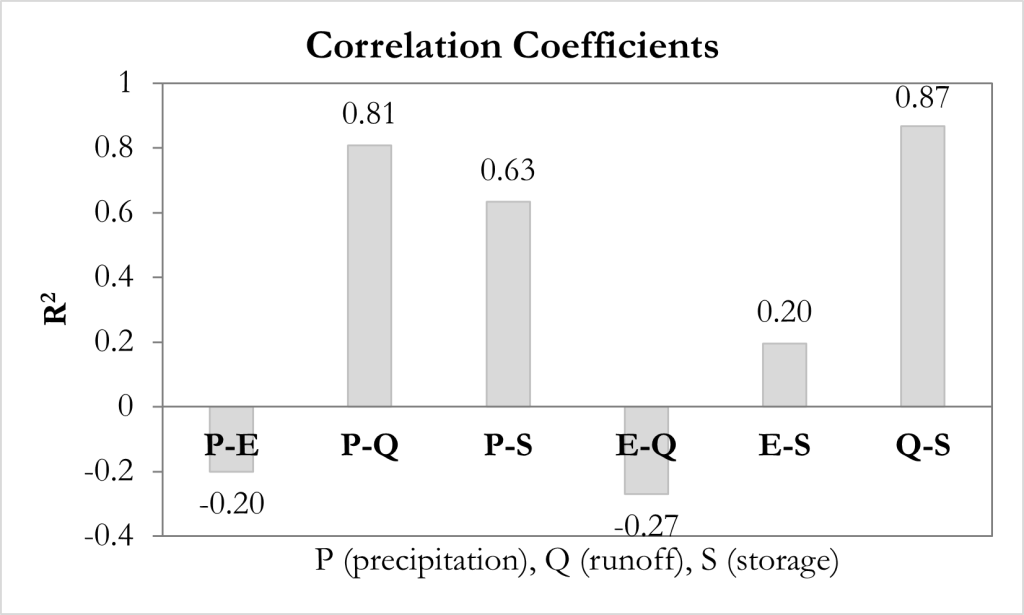
Se relacionarmos as correlações entre cada variável, chegamos em:

Competição entre Disponibilidade Hídrica e Evaporação

Retomando a equação do balanço hídrico e dividindo ambos os lados pela precipitação, obtemos:

$$ 1 = Q/P + E / P$$

onde $Q/P$ é a razão entre o escoamento superficial e a precipitação, definido como coeficiente de runoff e $E/P$ é a razão entre a evaporação e a precipitação da bacia, definido como o índice de aridez.

Assim, resolvendo a equação anterior para diversos valores de $E/P$ desde de 0 até $+ \infty$, construímos o seguinte gráfico:

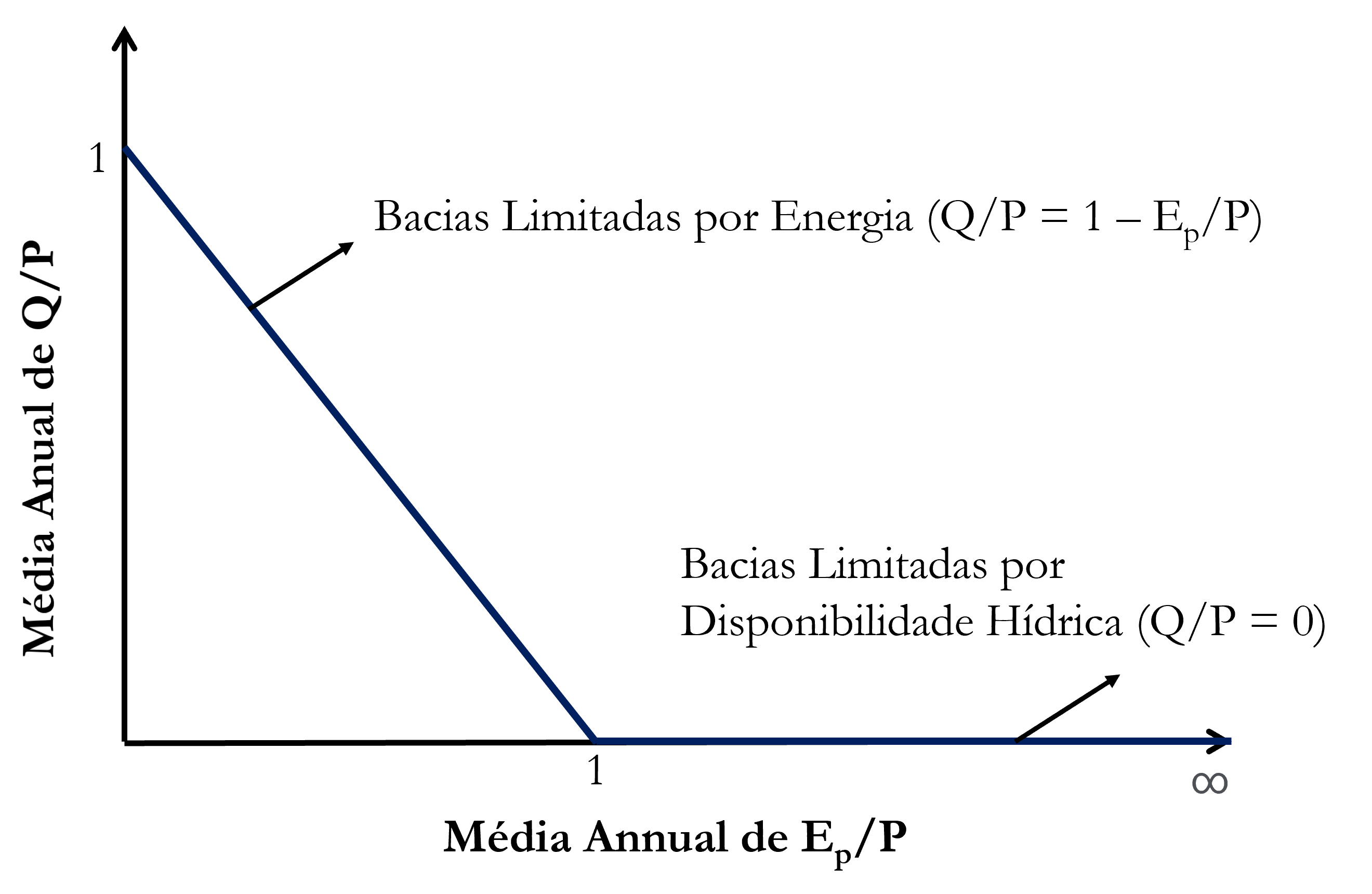
Esse é o modelo ideal caso apenas uma das forçantes seja limitada.

No entanto, na realidade, em muitos casos há a limitação de ambas forçantes ocorrendo simultaneamente, o que levanta a hipótese de que uma curva, superior a essa envoltória, seja necessária.

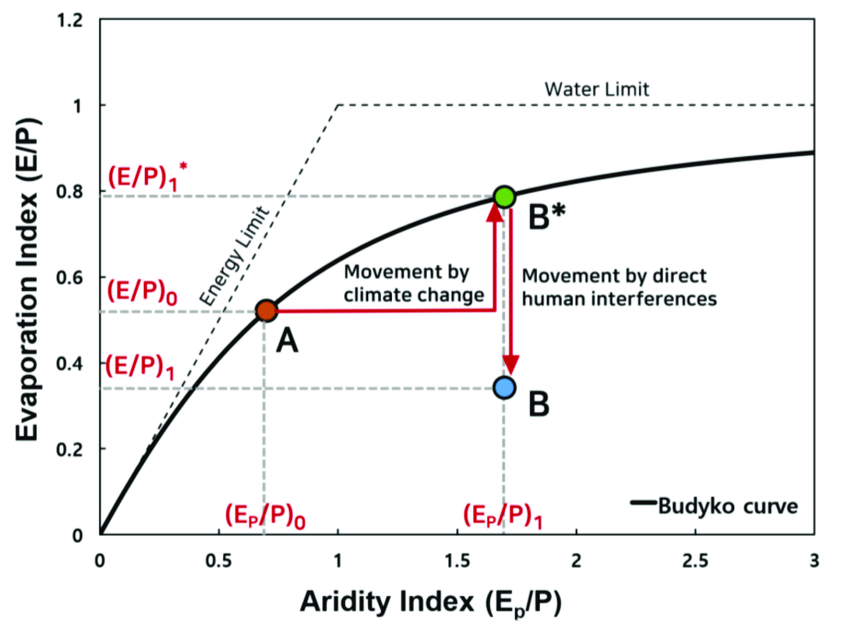
Observação de Budyko

Budyko foi um climatologista russo que percebeu que havia uma relação não linear entre o índice de aridez de uma bacia e sua geração de escoamento.

A partir de observações extensas da climatologia de diversas bacias ao redor do mundo, Budyko aproximou uma curva que explica a competição entre o índice de aridez e a disponibilidade hídrica, expressa pelo coeficiente de escoamento superficial.

Formulação de Budyko

$$
\frac{E}{P}=\left\{\frac{E_p}{P}\left[1-\exp \left(-\frac{E_p}{P}\right)\right] \tanh \left[\left(\frac{E_p}{P}\right)^{-1}\right]\right\}^{0.5}
$$  

onde a relação entre a evapotranspiração ou evaporação e a precipitação de uma bacia depende apenas do índice de aridez, que por sua vez é apenas função da climatologia local, isto é, da evapotranspiração potencial de uma área e de sua precipitação.

Exemplo 3

Uma bacia no Brasil tem índice de aridez atual de 0.7. Calcule a expectativa de produção de escoamento superficial apenas com essa informação.

Essa bacia tem expectativa de sofrer impactos das mudanças climáticas, o que eventualmente acarretaria a alteração do índice de aridez em 20% para cima, isto é, de 0.7 para 0.84. Além disso, estime a variação percentual do coeficiente de runoff em valores relativos.

Solução: 

Resolvendo a eq. de Budyko para Ep/P = 0.7, obtém-se E/P = 0.56 e, portanto, Q/P = 1 – E/P = 0.44

Ou seja, um indice de aridez de 0.7, que indica que a energia potencial de evaporação é capaz de evaporar 70% da precipitação, na verdade evapora 56% e produz 44% da precipitação como escoamento superficial.

Caso aumentemos o índice de aridez em 20%, o novo coeficiente de runoff passa a ser 37%, o que representa uma redução de 15%.

Conclusão

Nesse artigo é demonstrado uma forma rápida de se estimar a geração de escoamento superficial de uma bacia, dada sua simples climatologia de longo termo.

Além disso, a curva de Budyko tem sido usada extensivamente como um modelo alternativo à simulação complexa de todos fenomenos hidrológicos que acontecem em bacias hidrográficas.

Finalmente, apesar de simples, o modelo já foi validado e testado em milhares de bacias ao redor do mundo e, inclusive, recentemente nesse artigo elaborado em coautoria com colegas da USP São Carlos.