Rompimento de Barragens – Princípios da Modelagem Hidrodinâmica

O rompimento de barragens é um fenômeno altamente crítico que põe em risco não somente a sociedade, mas também todo o ecossistema envolvido.

Muitas vezes, inclusive, efeitos locais de rompimento de barragem são propagados por centenas de quilômetros à jusante, como foi o caso de Brumadinho, por exemplo.

O carreamento de rejeitos ao longo do curso hídrico receptor reduziu e contaminou abruptamente sua qualidade da água, que por sua vez impactou diversos setores que dependiam diretamente da fauna e flora associada ao recurso hídrico.

Sendo de uma importância extrema, o estudo dos impactos de rompimento de barragens hoje, especialmente no Brasil, é fundamental e necessário para definir estratégias de rápida adaptação perante a um evento dessa magnitude.

Assim, nesse artigo você irá aprender sobre como podemos elaborar estudos de modelagem hidrodinâmica para avaliar os efeitos do rompimento de barragens.

Introdução

De maneira geral, o movimento de um fluido ocorre de maneira tridimensional, isto é, ele conta com acelerações e velocidades que podem ter variações nas 3 direções principais.

Esse é o caso de uma pluma de poluente que se desloca no ar via uma chaminé, por exemplo.

No caso de fluidos como a água, por exemplo, é mais comum vermos sua propagação em uma ou duas direções predominantes.

O caso mais simples e geralmente o mais aplicado é o do escoamento em uma direção.

Nesses casos, o fluido tem acelerações e velocidades desprezíveis nas outras duas direções.

O caso mais típico desse escoamento é a propagação de cheias em canais, como ilustra a figura abaixo.

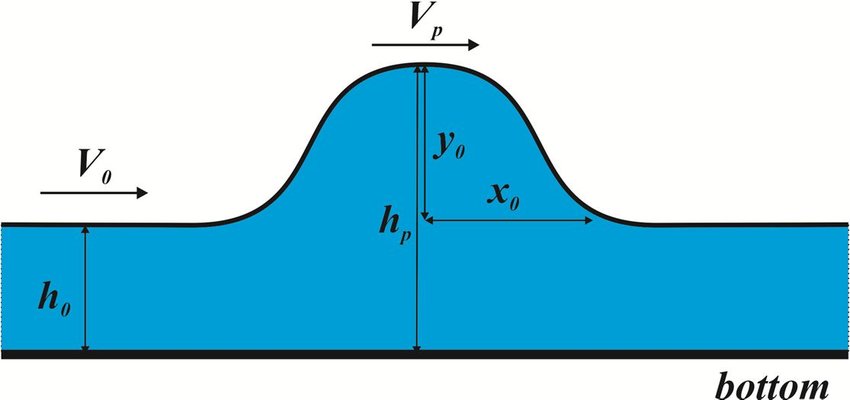
Naturalmente, é relativamente difícil de se explicar extravasamentos ou troca de fluido pelas laterais do canal, nos chamados overbanks, usando esse modelo.

Em casos onde as velocidades na outra direção do plano não são desprezíveis, é necessário um modelo 2D que pode contar com a parcela de velocidade e momento trocada nas laterais.

Nesse artigo, vamos detalhar o caso do escoamento unidimensional e em outros, vamos abordar o caso 2D.

Modelagem Hidrodinâmica 1D

A modelagem de rompimento de barragens 1D segue o mesmo princípio do caso onde modelamos a propagação de cheias em canais.

Apesar de se houver soluções analíticas para as equações hidrodinâmicas, em casos práticos, usa-se de uma solução numérica que discretiza essas equações em intervalos de tempo e de espaço discretos.

Simplificando as equações de Navier-Stokes no caso onde apenas a componente na direção do escoamento é importante, é possível de se chegar nas equações de Saint-Venant, descritas abaixo:

$$
\frac{\partial Q}{\partial x}+\frac{\partial A}{\partial t}= q_l
$$

$$
\frac{1}{A} \frac{\partial Q}{\partial t}+\frac{1}{A} \frac{\partial}{\partial x}\left(\frac{Q^2}{A}\right)+g \frac{\partial y}{\partial x}-g\left(S_o-S_f\right)=0
$$

Onde $A$ é a área molhada do canal, $Q$ é a vazão, $y$ é a altura d’água, $q_l$ é a vazão lateral por unidade linear de canal, $g$ é a aceleração da gravidade, $S_0$ é a declividade de fundo do canal e $S_f$ a declividade da linha de energia.

Detalhamento dos Termos da Equação

O termo $\frac{1}{A} \frac{\partial Q}{\partial t}$ representa o termo de aceleração local pois indica o grau de variação da vazão ao longo do tempo.

Já o termo $\frac{1}{A} \frac{\partial}{\partial x}\left(\frac{Q^2}{A}\right)$ representa a aceleração convectiva do escoamento, de modo que ela indica o quanto a vazão muda ao longo do comprimento do canal. Mesmo em regime permanente, a velocidade pode mudar ao longo do comprimento do canal e, portanto, essa parcela pode ser não nula. 

Já o termo $g \frac{\partial y}{\partial x}$ representa o termo de pressão hidrostática da água e, finalmente, o termo $g\left(S_o-S_f\right)$ representa o equilibrio ou não entre as forças gravitacionais (expressas por $s_o$) em relaçao as forças de fricção (expressas por $s_f$).

A equação anterior é do tipo diferencial parcial hiperbólica e, de novo, só tem soluções analíticas para casos muito particulares que fogem muitas vezes da realidade de uma aplicação prática.

Desse modo, para resolvê-la, podemos usar uma solução numérica que a discretiza no espaço $x$ e no tempo $t$.

Discretização Numérica

De maneira geral, imagine uma malha onde o eixo x é o eixo do canal, discretizado em intervalos $\Delta x$ e no  eixo $y$ é o tempo, discretizado em intervalos $\Delta t$.

A solução da equação no tempo $t$ pode ser escrita como função explícita, isto é, dependendo apenas do tempo $t – \Delta t$ ou de forma implicita onde um sistema de equações não lineares deve ser resolvido a cada time-step.

Para não ficar um artigo muito técnico e matemático vou parando a burocracia e papo de nerd por aqui, e, caso você queira, você pode se aprofundar mais.

Veja um artigo meu que trata exatamente sobre a criação de um modelo que discretiza essa equação.

Link do artigo – https://www.sciencedirect.com/science/article/pii/S1364815223001196

 

Assim, a qualidade da discretização do espaço e do tempo está totalmente ligado com o detalhamento da solução numérica.

Toda solução numérica tem erros e esses erros são minimizados quanto melhor for a discretização da malha computacional usada para resolver as equações diferenciais.

Aproximações das Equações de Saint-Venant

A solução das equações completas é as vezes computacionalmente desafiadora e, em alguns casos, demasiadamente detalhada dada a natureza do fenomeno do escoamento estudado.

Assim, diversas simplificações podem ser feitas levando em conta os fenômenos preponderantes no escoamento.

A escolha da aproximação adequada depende do conhecimento prévio do sistema.

Por exemplo, em canais de alta declividade, o uso de modelos cinemáticos que levam em conta o efeito da gravidade como critério principal pode ser uma boa e simples aproximação.

Logo abaixo vamos ver um detalhe dessas simplificações.

Dados de Entrada

Para se resolver soluções hidrodinâmicas de rompimento de barragem é necessário alguns dados de entrada como:

• Seções transversais razoavelmente espaçadas para que se consiga capturar mudanças importantes na topografia
• Declividade entre duas seções transversais
• Coeficientes de rugosidade de Manning, que pode ser um só por seção ou pode ter valores variando com a altura ou com as áreas de várzea
• Condições de contorno de entrada, que pode ser um ou vários hidrogramas de entrada, bem como uma série observada de níveis d’água em nós específicos da malha
• Condição de contorno de ruptura da barragem. Nesse caso, um hidrograma de falha ou de brecha pode ser usado para simular a entrada de água dentro do domínio do canal.
• Condições de contorno do exutório, que pode trabalhar em regime normal, crítico ou com cota conhecida ao longo do tempo

De maneira simplificada, precisamos ter uma fonte de “entrada” de água, um modo de controlar essa “saida” de água do domínio e um modo de computar as resistências que a água vai sofrer ao se propagar ao longo da planície de inundação de jusante da barragem.

Programas de Análise

Programas que resolvem as equações de Saint-Venant completas são bons candidatos. A exemplo temos:

• Stormwater Management Model (SWMM). Apesar de ser para drenagem urbana, seu solver das equações de águas rasas pode ser usado para avaliar a propagação da onda de cheia. Download disponível em: https://www.epa.gov/water-research/storm-water-management-model-swmm
• Hydrologic Engineering Center River Analysis System (HEC-RAS 1D). Esse é um ótimo candidato para avaliar a propagação 1D de ondas de cheia. Download disponível em: https://www.hec.usace.army.mil/software/hec-ras/download.aspx
• Softwares de linguagem aberta como o desenvolvido por mim nesse artigo, disponível na minha conta do github aqui.

Processo de Calibração e Validação

Todo modelo tem incertezas. Na verdade, é argumentável que precisaríamos de uma memória infinita nos computadores para que consigamos rodar um modelo de precisão infinita.

Assim, é papel do engenheiro(a) avaliar a aptidão de seu modelo em representar a realidade.

Desse modo, uma maneira corriqueira de se avaliar a qualidade do modelo é compará-lo com observações de vazões, níveis, velocidades ou qualquer outra variável de estado observada no exutório ou em pontos internos do domínio.

O processo de calibração consiste definir, seguindo uma lógica ou aleatoriamente, os parâmetros do modelo de modo que seus resultados se aproximem o máximo possível das observações.

Não é foco desse artigo aqui, mas é verdade que uma combinação infinita de parâmetros pode produzir resultados iguais ou muito parecidos.

Esse fenômeno é chamado de equifinalidade, que também fora recentemente estudado em texto elaborado por mim, em revisão e disponível aqui.

Assim, é importante lembrarmos de adotar parâmetros que estejam dentro da física do problema; caso contrário teremos modelos calibrados mas que fogem da realidade quando validados.

A validação, por sua vez, consiste na aplicação do modelo para intervalos de observação fora dos dados usados para calibrar o modelo.

O objetivo dessa etapa é descobrir se o modelo não somente consegue representar aquilo que lhe fora dado como informação para seu ajuste, mas também se ele tem sua principal função, isto é, a função de prever o comportamento do sistema fora das observações usadas para sua calibração.

Pros e Contras da Modelagem 1D

Algumas dicas das vantagens e desvantagens dessa abordagem já pode ser mais ou menos inferidas da teoria passada nos tópicos anteriores.

Primeiro modelos 1D são mais simples.

Desse modo, absolutamente mais rápidos que modelos 2D e 3D, o que pode ser uma grande vantagem, especialmente em sistemas em que uma resposta rápida é precisa para uma tomada de decisão.

Além disso, modelos 1D requerem menos dados detalhados sobre a topografia, uma vez que o levantamento de algumas seções transversais tende a ser mais barato que um levantamento em LiDAR de uma área extensa de interesse onde a onda de cheia pode se propagar.

No entanto, modelos 1D tem problemas importantes quando áreas de várzea começam a interferir na hidrodinâmica da propagação. 

Além disso, quando bifurcações excessivas com desníveis entre os canais começam a ser importantes, modelos 1D podem sofrer muito com problemas de instabilidade numérica.

Por muitas vezes usar-se de soluções implícitas das equações, modelos 1D devem ter critérios de estabilidade rígidos para garantir a acurácia da solução numérica.

Apesar dessas desvantagens, essa é ainda uma alternativa relativamente barata para a elaboração de estudos hidrodinâmicos, especialmente os estudos relacionados ao rompimento de barragens.

Em outro artigo vamos abordar esses mesmos tópicos mas sob a ótica de modelos 2D.

Exemplo – Modelagem de Brumadinho (2019)

Nesse examplo vou lhe mostrar uma aplicação de um modelo unidimesional (HydroHP-1D) para a avaliação hidrodinâmica do rompimento da barragem de brumadinho. 

Mais detalhes dessa abordagem podem ser vistos nesse pre-print do artigo em revisão.

Brumadinho foi parametrizada em modelada assumindo seções transversais espaçadas e levantadas antes do rompimento da barragem.

Os coeficientes de Manning foram calibrados a partir de observações do tempo de chegada da onda de cheia e de sua altura, em algums pontos à jusante da barragem.

Perfil lateral da superfície da linha d’água, velocidade do escoamento e força hidrodinâmica de arrasto

Vista superior da onda de cheia e perfi lateral da superfície da linha d’água.

Conclusões

O estudo do impacto do rompimento de barragens requer o uso de modelos hidrodinâmicos.

Uma das modalidades de modelo mais usadas são os modelos unidimensionais, isto é, modelos que assumem que a onda de cheia propaga-se predominantemente em uma única direção

Nesse artigo vimos o princípio, os dados de entrada, a base da calibração e validação, bem como alguns softwares disponíveis e as vantagens e desvantagens dessa abordagem.

Em outros artigos abordaremos as mesmas características, mas para modelos 2D.