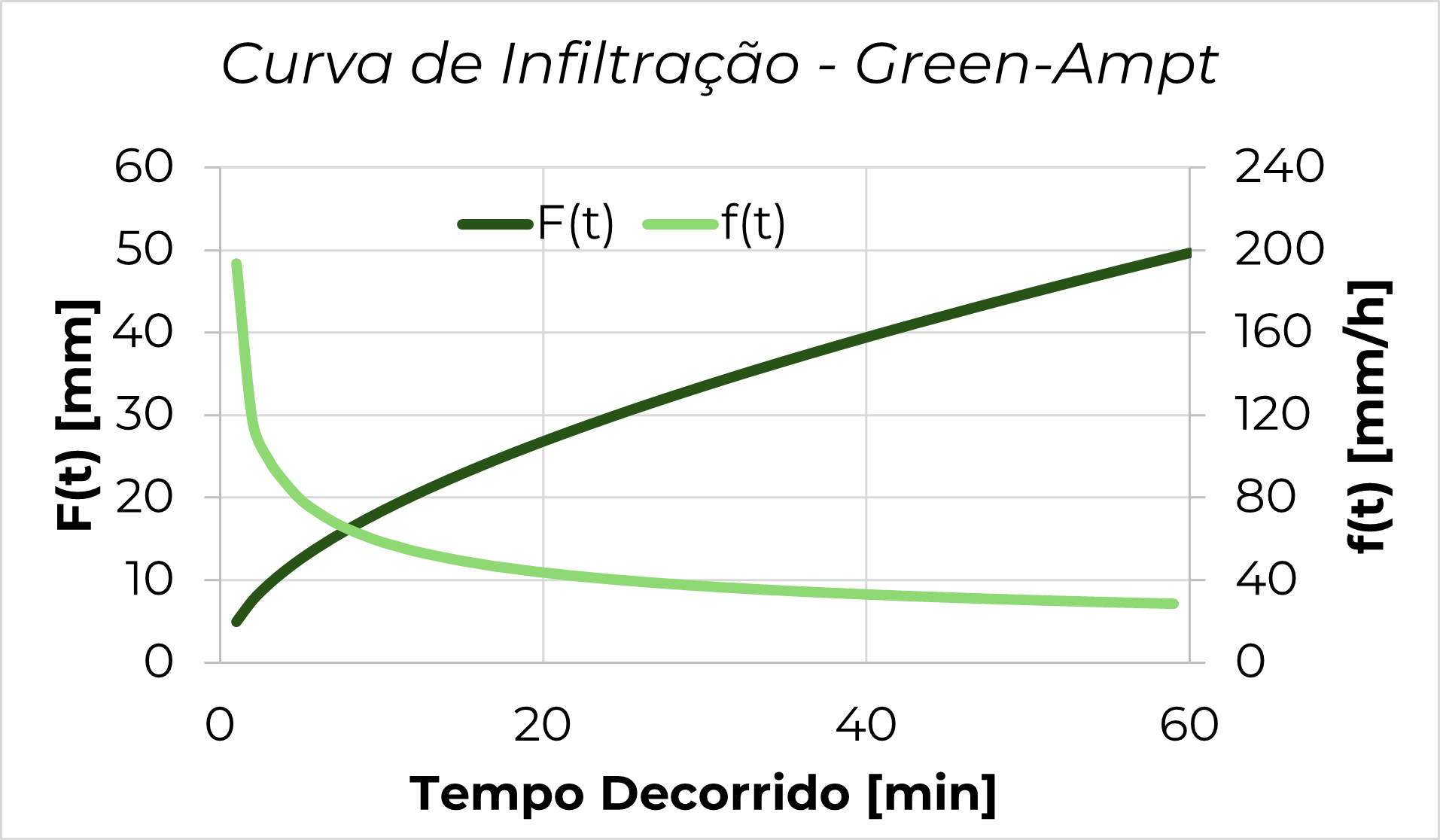
Modelo de Infiltração – Green-Ampt
O Modelo de Infiltração de Green-Ampt representa uma contribuição significativa para a compreensão matemática do movimento da água no solo.
Até então, 1911, apenas o modelo de Darcy houvera sido proposto e servira de base para a formulação de Green-Ampt
Este modelo, desempenha um papel crucial na Engenharia Hidrológica, especialmente na análise de geração de escoamento superficial.
Importância do Modelo de Green-Ampt
A importância do Modelo de Green-Ampt reside na sua capacidade de proporcionar uma abordagem matemática relativamente precisa e fisicamente baseada para o fenômeno complexo e não-linear da infiltração de água no solo, considerado um meio poroso.
Ao considerar fatores como a condutividade hidráulica, porosidade do solo e pressão de sucção, o modelo oferece uma visão detalhada do processo de entrada da água no solo.
Um modelo de base física, mas ainda assim simples
O Modelo de Green-Ampt destaca-se como um dos mais utilizados na Engenharia Hidrológica devido à sua simplicidade, precisão e aplicabilidade em uma variedade de contextos.
Sua capacidade de modelar eficientemente a infiltração torna-o uma ferramenta versátil, aplicada em estudos hidrológicos, gestão de recursos hídricos, projetos de drenagem e diversas outras áreas.
Princípios Básicos e Formulação do Modelo de Green-Ampt
O modelo de Green-Ampt é uma simplificação do processo de infiltração de água no solo, especialmente em relação a como a frente de umedecimento é concebida.
Imaginando um pistão que se desloca verticalmente para baixo, o modelo de Green-Ampt considera haver uma frente bem definida onde a separação entre o que é não saturado e o que é saturado é bem clara.
Essa franja, ou frente, é chamada de frente de sucção. Nela, é assumido que uma pressão $-\psi$ é exercida e o deslocamento dessa frente para a direção vertical para baixo é função da condutibilidade hidráulica saturada ($K_{sat}$).
Vamos imaginar que, num determinado instante, o perfil de saturação do solo encontra-se assim:
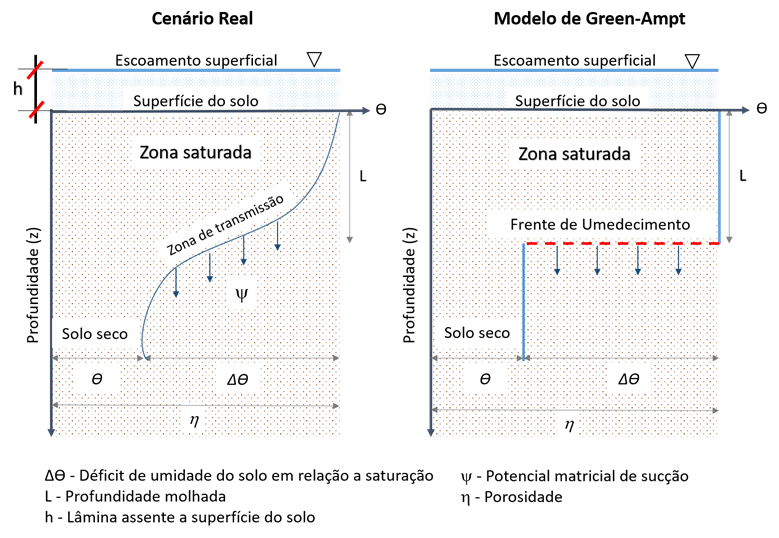
A linha azul curvilínea na figura à esquerda é o perfil real de saturação, que mostra uma não-linearidade do teor de umidade em relação à altura do solo.
Na aproximação de Green-Ampt, essa frente é solidária, horizontal e plana, deslocando-se verticalmente para baixo sem essa curvatura do caso real.
A variável $\eta$ representa a porosidade do meio poroso, enquanto a umidade residual é expressa por $\theta$ e a porosidade efetiva por $\Delta \theta$.
O gradiente hidráulico, isto é, a diferença de pressão total entre o topo da camada superior com água acumulada até a frente de umedecimento é
$$ \Delta h = h + L + \psi $$
onde $\psi$ é o potencial matricial de sucção do solo.
Já a lei de Darcy em meios porosos saturados é dada por:
$$f = k_{\mathrm{sat}} \Bigl( \frac{\Delta h}{L} \Bigr)$$
onde o gradiente hidráulico é denotado por $ \frac{\Delta h}{L}$ e mede a perda de carga por unidade de comprimento que o fluído passa no meio poroso.
Aplicando-se a lei de Darcy em meios porosos, obtemos assim a equação de Green-Ampt, que fora desenvolvida em 1911.
$$ f = k_{\mathrm{sat}} \frac{(h + L + \psi)}{L} $$
Rearranjando-a e assumindo $L = F \Delta \theta$, temos que:
$$ f = k_{\mathrm{sat}} \Bigl( 1 + \frac{(h + \psi) \Delta \theta}{F} \Bigr)$$.
Assumindo que a infiltração vai seguir igual a capacidade de infiltração, isto é, a intensidade de precipitação é maior ou igual a capacidade de infiltração, podemos escrever que ela é $f = \frac{\mathrm{d}F}{\mathrm{d}t}$, e finalmente separar as variáveis e integrar:
$$\int_{F(t_0)}^{F(t)} \frac{F(t)}{F(t)+(h + \psi) \Delta \theta} d F=\int_{t_0}^t k_{\mathrm{sat}} d t$$
Resultando na seguinte expressão implícita que deve ser resolvida por tentativa e erro ou por métodos de gradiente como o método de Newton-Raphson.
$$ F(t)=k_{\mathrm{sat}} (t – t_0)+(h + \psi) \Bigl( \Delta \theta \ln \left[1+\frac{F(t)}{(h + \psi) \Delta \theta}\right] – \Delta \theta \ln \left[1+\frac{F(t_0)}{(h + \psi) \Delta \theta}\right] \Bigr) + F(t_0)$$
A equação anterior assume que o tempo inicial da simulação não é 0 e nem que a infiltração acumulada inicial também não é nula. Nos casos em que ambos são nulos, a equação se resume em:
$$F(t)=k_{\mathrm{sat}} t+\psi \Delta \theta \ln \left[1+\frac{F(t)}{\psi \Delta \theta}\right]$$
Exemplo
Determine a curva de infiltração acumulada e taxa de infiltração em uma parcela de solo que recebe fluxo constante.
Dados:
$\psi = 210$ mm
$\Delta \theta = 0.437 $
$k_{\mathrm{sat}}$ = 10 mm /h
$ h = 0$
$F(t_0) = 5$ mm
$t_0 = 1$ min
$\Delta t = 1$ min
$t = 60$ min
Solução.
A equação de infiltração acumulada pelo método de Green-Ampt é implícita e requer algoritmos de cálculo numérico para sua solução.
Felizmente o Excel conta com um deles, o GRG não-linear. Para isso, vamos configurar o problema no excel e tentar igualar os lados esquerdo e direito de todas as equações indo do tempo $ t = 1$ até $t = 60$.
Setando o solver do excel para decidir quais são os respectivos valores de $F(t)$, com $t = 1$ até $60$, ou seja, 59 variaveis de decisão, e colocando-o para minimizar a soma do erro quadrático entre os valores modelados (lado direito da equação) e escolhidos (lado esquerdo), chegamos na curva de infiltração.
Para calcular a taxa de infiltração entre dois intervalos de tempo, basta fazer $f = dF/dt \approx \Delta f / \Delta t$ e ir calculando a cada dois intervalos.
O resultado final é apresentado como:
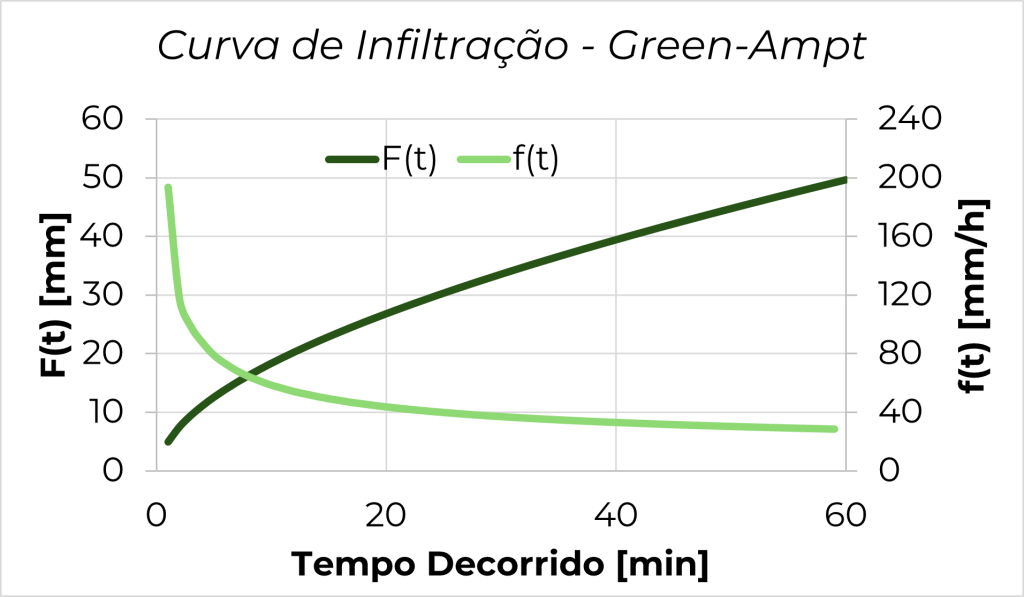
Para baixar a planilha, clique aqui.
