Lei de Darcy em Meios Porosos
Darcy, o mesmo da equação de Darcy-Weisbach para cálculo do fator de atrito em redes pressurizadas, foi um engenheiro francês que viveu no século 19.
Henry Darcy formulou, em seus últimos anos de vida antes de contrair pneumonia, a Lei de Darcy.
A Lei de Darcy é o princípio básico da formulação moderna de escoamento em meios porosos. Vários softwares como por ex o MODFLOW tem por princípio a formulação elaborada por Darcy em 1856.
Mais adiante, novos modelos mais completos de infiltração como o Modelo de Richards ou o Modelo de Green-Ampt foram desenvolvidos tendo a Lei de Darcy como princípio.
Assim como Isaac Newton dissera para Robert Hook, “Se cheguei até aqui foi porque me apoiei no ombro de gigantes”, Richards e Green-Ampt estão para Darcy assim como Newton está para Hook.
Se quiser saber mais sobre o método de Green-Ampt, veja esse artigo abaixo.
Darcy, em sua publicação original, explicita:
Os experimentos demonstram positivamente que o volume de água que passa por um leito de areia de determinada natureza é proporcional à pressão e inversamente proporcional à espessura do leito percorrido.
Introdução a formulação da Lei de Darcy
Imaginemos que um meio poroso recebe um fluxo $Q$ e esse fluxo se desloca uma distância $\Delta L$.
No meio poroso, o atrito do fluido com as partículas gera perda de energia de modo que se medirmos a pressão num ponto 1 ($h_1$) e depois em um ponto 2 ($h_2$), o gradiente de pressão é:
$$ j = \frac{\Delta P}{\Delta L} = \frac{h_2 – h_1}{\Delta L} $$
Darcy observou que:
$$ q \sim \Delta P $$
e que
$$ q \sim \frac{1}{\Delta L} $$
Logo:
$$ q \sim j $$
A constante de proporcionalidade dessas relações é justamente a condutibilidade hidráulica saturada, no caso do fluxo de água ($k_{\mathrm{sat}})$.
A figura baixo representa o esquema do experimento de Darcy.
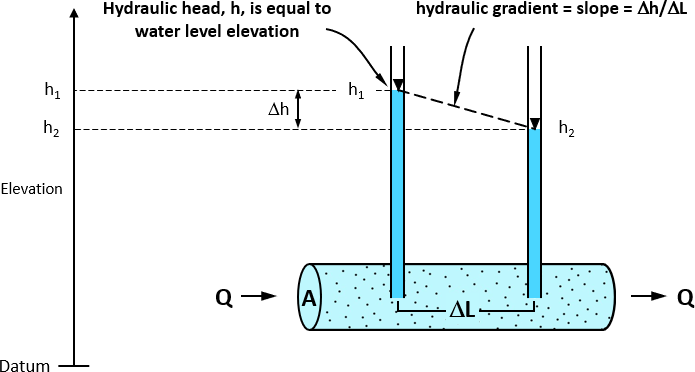
A velocidade, ou taxa de infiltração $q$, nada mais é que a vazão $Q$ dividida pela área de escoamento $A$, de modo que:
$$ Q = -k_{\mathrm{sat}}A \Bigl(\frac{\Delta P}{\Delta L}\Bigr)$$
onde o sinal negativo serve para considerar que a pressão decresce ao longo do comprimento do meio filtrante.
Finalmente, de maneira diferencial, podemos escrever a lei de darcy como:
$$ Q = -k_{\mathrm{sat}}A \Bigl( \frac{\mathrm{d}h}{\mathrm{d}L} \Bigr) $$
Exemplo Prático
Determine a taxa de infiltração em um poço de infiltração inclinado, 45 graus com a horizontal, composto por areia com condutibilidade hidráulica saturada de 20 cm/h e altura de 1.20 m. Assuma que o lençol freático encontra-se bem profundamente.
Determine o tempo necessário para filtrar $1~\mathrm{m^3}$ de água se a área de seção transversal é $20~\mathrm{m^2}$.
Solução
A taxa de infiltração é:
$$ q = -k_{\mathrm{sat}} \Bigl( \frac{\mathrm{d}h}{\mathrm{d}L} \Bigr) \approx -k_{\mathrm{sat}} \Bigl(\frac{\Delta P}{\Delta L}\Bigr)$$
$$ q = -20 \frac{(0 – 120)}{120 \sqrt{2}} $$
$$ q = 14.14~\mathrm{cm/h}$$
ou seja, cerca de 14.14 cm de água se deslocam em 1h no perfil inclinado de area, o que resulta numa vazão de:
$$ q = Q/A \rightarrow Q = q \times A$$
$$ Q = 14.14 \times 2 \times \frac{1}{100} \times \frac{1}{1000} \times \frac{1}{3600} = 0.078~\mathrm{L/s}$$
O tempo para infiltrar $1~\mathrm{m^3}$ é
$$ t = \frac{V}{Q} = 1000 / (0.078) = 12820~\mathrm{sec} = 3.56~\mathrm{h}$$
