Distribuições Empíricas de Probabilidade – Hidrologia Estatística
As distribuições empíricas de probabilidade visam explicar como os dados de chuva, ou qualquer outra variável aleatória, se adequam a uma determina equação de distribuição de probabilidade.
De maneira geral, as equações de distribuição empírica de probabilidade podem ser escritas da seguinte forma:
$$\mathrm{Prob}(x \geq x_m) = \frac{m-b}{n + 1 – 2b}$$
Lê-se (Probabilidade da variável aleatória x ser maior ou igual ao valor $x_m$).
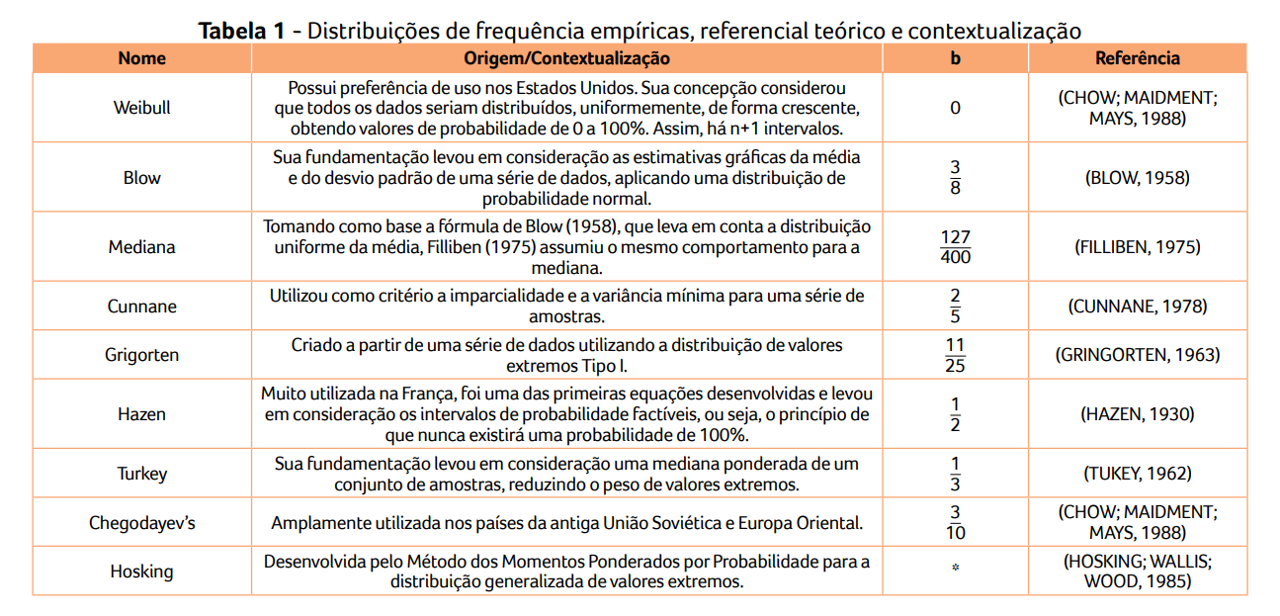
onde $x_m$ representa um determinado valor de precipitação esperada, $m$ é m-ésima ordem crescente da série de precipitações, $n$ é o tamanho da amostra e $b$ é dado pela seguinte tabela:
Exemplo) Tempo de Retorno por Distribuições Empíricas de Probabilidade
Dada uma série história com os valores de precipitação de 100, 120, 90, 150, 200, 75, 125, 50, 90 e 110 mm de máximos anuais, calcule o tempo de retorno empírico de uma precipitação de 90 mm pelos métodos Weibull, Mediana e Califórnia. O método Califórnia simplesmente assume que a probabilidade é $\mathrm{Prob}(x \geq x_m) = \frac{m}{n}$
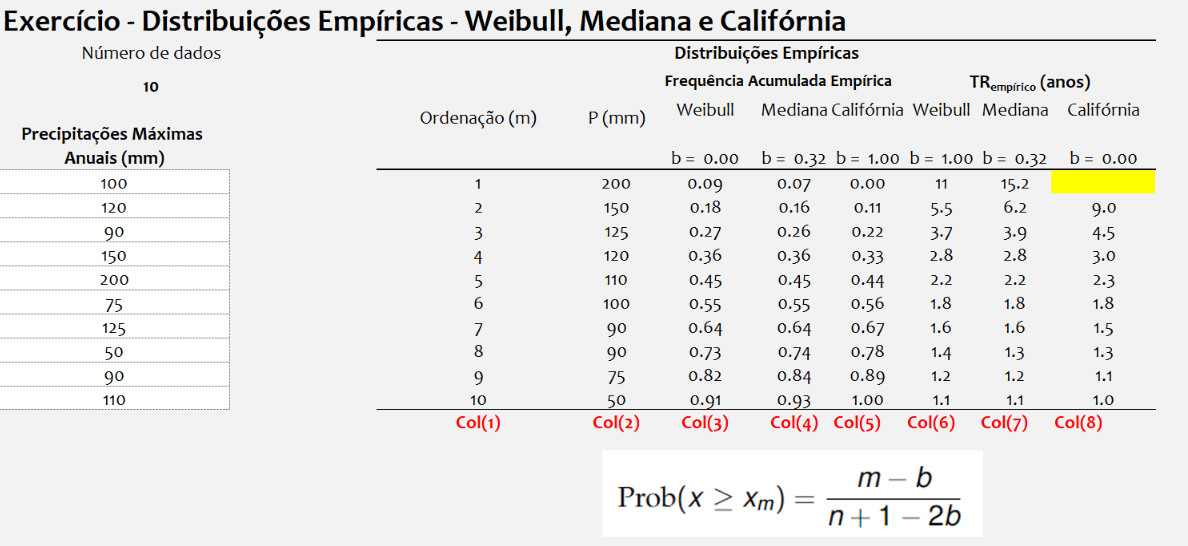
Col(1): Ordenação do maior para o menor.
Col(2): Valores ordenados de precipitação.
Col(3) – Col(4): Frequência acumulada pelos métodos de Weibull, Mediana e Califórnia, respectivamente.
Col(6) – Col(8) tempos de retorno calculados usando a expressão $\mathrm{TR} = 1/(\mathrm{Prob(x \geq x_m)})$.
Perceba haver uma indeterminação para o método da Califórnia para $m = 1$. Isso é facilmente observado por sua expressão.
Graficamente, os resultados ficam:
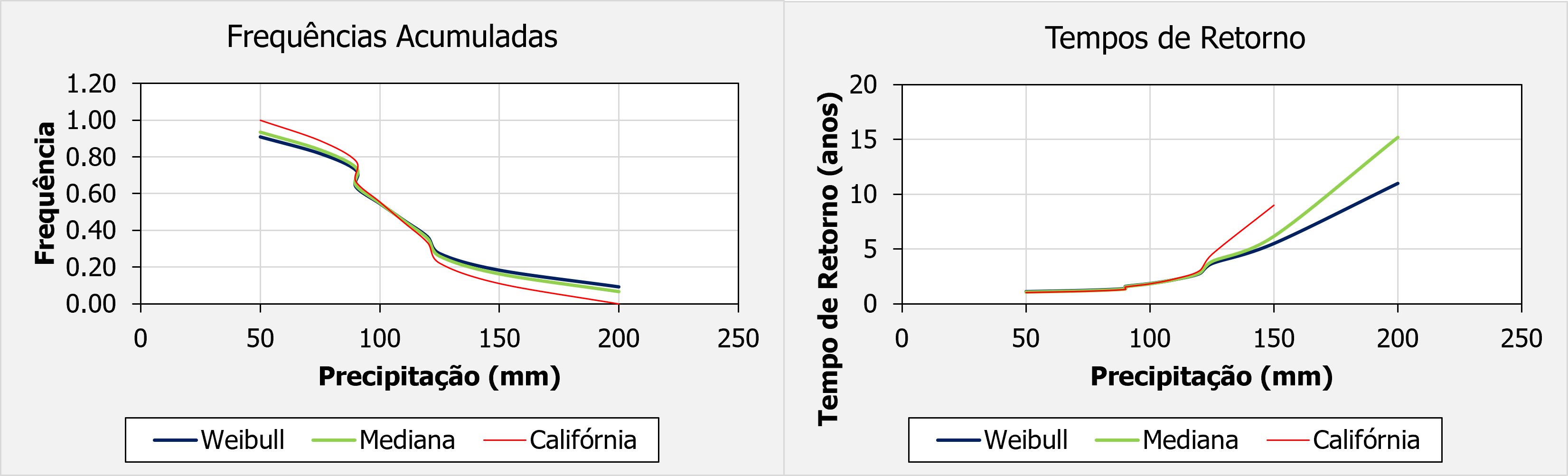
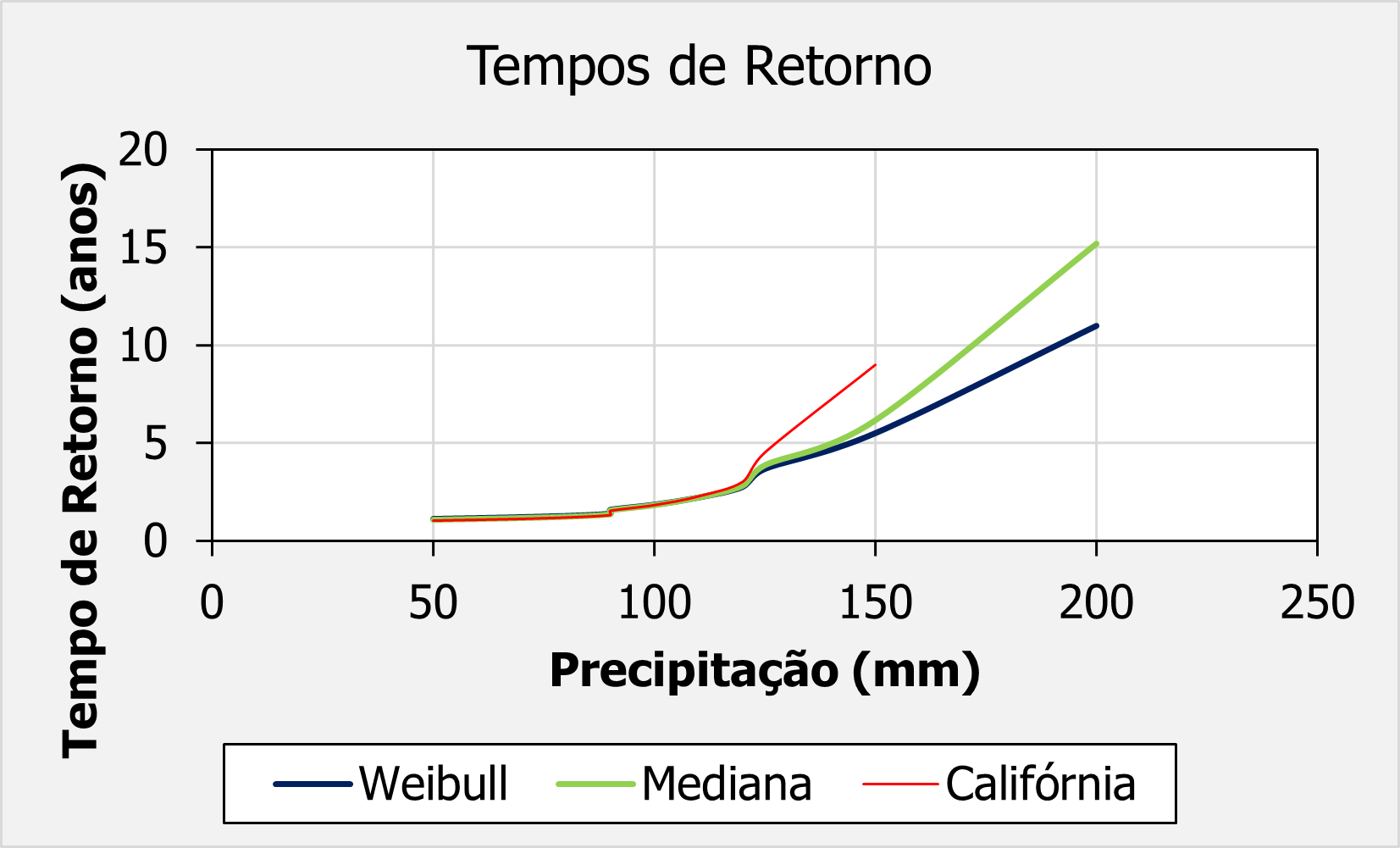
Perceba que para tempos de retorno baixos, os métodos se aproximam bem.
No entanto, para tempos de retorno mais altos, uma grande discrepância nos métodos é observada, sendo o método de Weibull consistentemente o que dá menores tempos de retorno para uma dada precipitação e o de califórnia dando o maior valor.
Ok, pronto, temos um método para estimar o tempo de retorno
Mas e se eu te perguntasse: Qual a precipitação com tempo de retorno de 100 anos, ou qual a precipitação com tempo de retorno de 0.5 anos?
Esses valores definitivamente não são expressos por métodos de distribuição empíricos, especialmente se o tamanho da amostra é limitado.
Além disso, como você determina a probabilidade de um evento que não é exatamente um dos dados da amostra? Talvez você tenha que interpolar valores.
Essa são algumas das desvantagens de distribuições empíricas de probabilidade.
Parece lógico que seria interessante termos uma expressão contínua e analítica para determinar a probabilidade de falha ou tempo de retorno para um dado valor da variável aleatória.
Por isso, nos próximos artigos, vamos aprender métodos estatísticos para determinar valores de nossa variável aleatória para riscos ou frequências acumuladas, ou probabilidades de excedência, além do intervalo de origem da distribuição.
