Fundamentos Básicos de Hidrologia Estatística
Dados de precipitação podem ser fornecidos em escalas diárias ou sub-diárias
No Brasil, exceto em grandes centros urbanos como São Paulo e outras capitais, a maioria dos dados disponíveis são de precipitações diárias.
Para o ajuste de curvas de intensidade-duração-frequência, primeiro devemos obter os valores máximos de precipitação anual.
A mesma análise valeria para um rio em que queiramos, por exemplo, determinar a vazão para um dado tempo de retorno.
Nos dados de precipitações máximas anuais, indicadores estatísticos como Média, Desvio Padrão, Coeficiente de Variância, Coeficiente de Assimetria, Máximo, Mínimo e o intervalo dos histogramas são alguns dos mais comuns em análises de extremos.
Média, Desvio Padrão e Coeficiente de Assimetria
Média
No excel, podemos usar as fórmulas $\texttt{average}$ ou $\texttt{média}$, selecionado a série de dados como entrada nas funções.
Desvio Padrão
Similarmente, podemos usar a função $\texttt{STD.S}$ e $\texttt{DESV.PAD}$ para o cálculo do desvio padrão amostral. Cabe notar que o desvio padrão populacional difere do amostral por ter no denominador um número igual a $n – 1$ ao invés de $n$.
Coeficiente de Assimetria
Para o Coeficiente de Assimetria podemos utilizar a função $\texttt{SKEW}$.
$$S = \frac{1}{s n}\sum_{i=1}^{n}\Bigl(x_i – \bar{x} \Bigr)^3$$
onde $s$ é o desvio padrão, $x_i$ é o i-ésimo dado de precipitação, $n$ é o tamanho da amostra e $\bar{x}$ é o valor médio de precipitações máximas anuais.
Coeficiente de Variação, Máximo, Mínimo
Coeficiente de Variação
$c_v$ é dado pela razão entre o desvio padrão e a média, escrito como:
$$c_v = \frac{s}{\bar{x}}$$
No excel calculamos resolvendo a equação anterior algebricamente.
Máximos e Mínimos
Os valores de máximos e mínimos são dados pela função $\texttt{max}$ ou $\texttt{máximo}$ para valores de máximo e $\texttt{min}$ ou $\texttt{mínimo}$ para valores de mínimo.
Tempo de Retorno
O tempo de retorno, ou algumas vezes chamado de tempo de recorrência, é uma duração, em anos, em que, em média, um evento é igualado ou superado, pelo menos uma vez.
O tempo de retorno é uma variável positiva, maior que zero, que vai até o infinito.
Um tempo de retorno de 1 ano significa que, em média, o evento associado com esse tempo de retorno ocorre pelo menos uma vez por ano.
Matematicamente, escrevemos:
$$ \mathrm{TR} = 1/f$$
onde $f$ é a frequência acumulada do evento associado
Frequência e Frequência Acumulada
Frequência é a quantidade de vezes que um determinado evento ocorreu em uma série histórica
Por exemplo, qual a frequência de chuvas maiores que 100 mm na série $\mathbf{S} = $ [200, 98, 35, 23, 101] mm?
A frequência é 2 pois dois eventos maiores que 100 mm ocorreram
Já a frequência acumulada é a razão entre a frequência e o número de observações, isto é, $$f = F/n$$ onde $F$ é a frequência do evento e $n$ o número de observações.
Histograma de Frequências
Histograma é um gráfico que relaciona a frequência que cada intervalo de uma variável aleatória tem
Por exemplo, veja a figura abaixo:
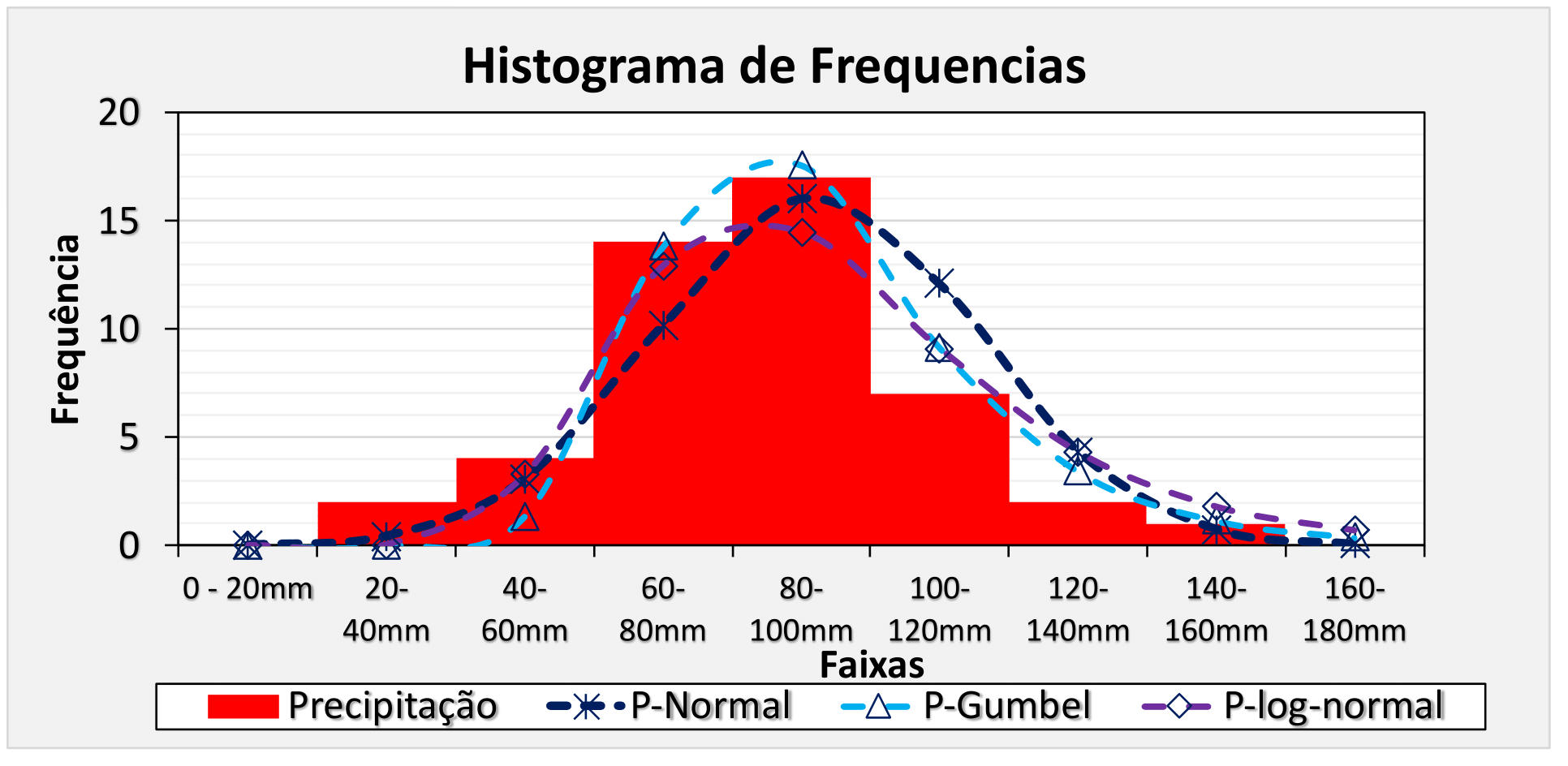
Ele relaciona a precipitação e o número de vezes que ocorreu um valor de precipitação no intervalo adotado (bin)
Intervalo de Histogramas (bins)
O intervalo de um histograma de dados geralmente é calculado pela seguinte razão:
$$k_{\mathrm{min}} = \sqrt{n}$$
Porém, muitas vezes $k_{\mathrm{min}}$ não é inteiro, tampouco múltiplo de um valor usual (e.g., 10 ou 20 mm)
Exemplo 1 – Aplicação dos Fundamentos Básicos de Hidrologia Estatística
Determine todas as estatísticas descritivas da seguinte amostra:
$\mathbf{P} = [100,~120,~90,~150,~200]^T$
Exemplo 2
Determine o intervalo de discretização de um histograma de frequências com 10 para a seguinte série de precipitações observadas nos últimos 10 anos em uma estação pluviométrica
