Desagregação de Chuva e Coeficientes de Desagregação – Hidrologia Estatística
Apesar de muitas vezes trabalharmos com dados diários de precipitação, curvas IDF são geralmente utilizadas para chuvas sub-diárias (e.g., 2h, 30-min, 12h)
Desse modo, surge a pergunta:
Como estimar dados de inexistentes de precipitação sub-horária a partir de dados diários de precipitação?
Podemos responder essa pergunta com os coeficientes de desagregação.
Naturalmente, a relação entre a chuva diária e a chuva sub-horária depende de muitos parâmetros e principalmente da localidade do estudo, isto é, do padrão de chuvas da área de estudo.
Entretanto, muitas vezes aplicamos, ao menos para o Estado de São Paulo, os coeficientes propostos pela CETESB.
A figura abaixo representa um fator de conversão de um valor de chuva diário em um valor sub-diário.
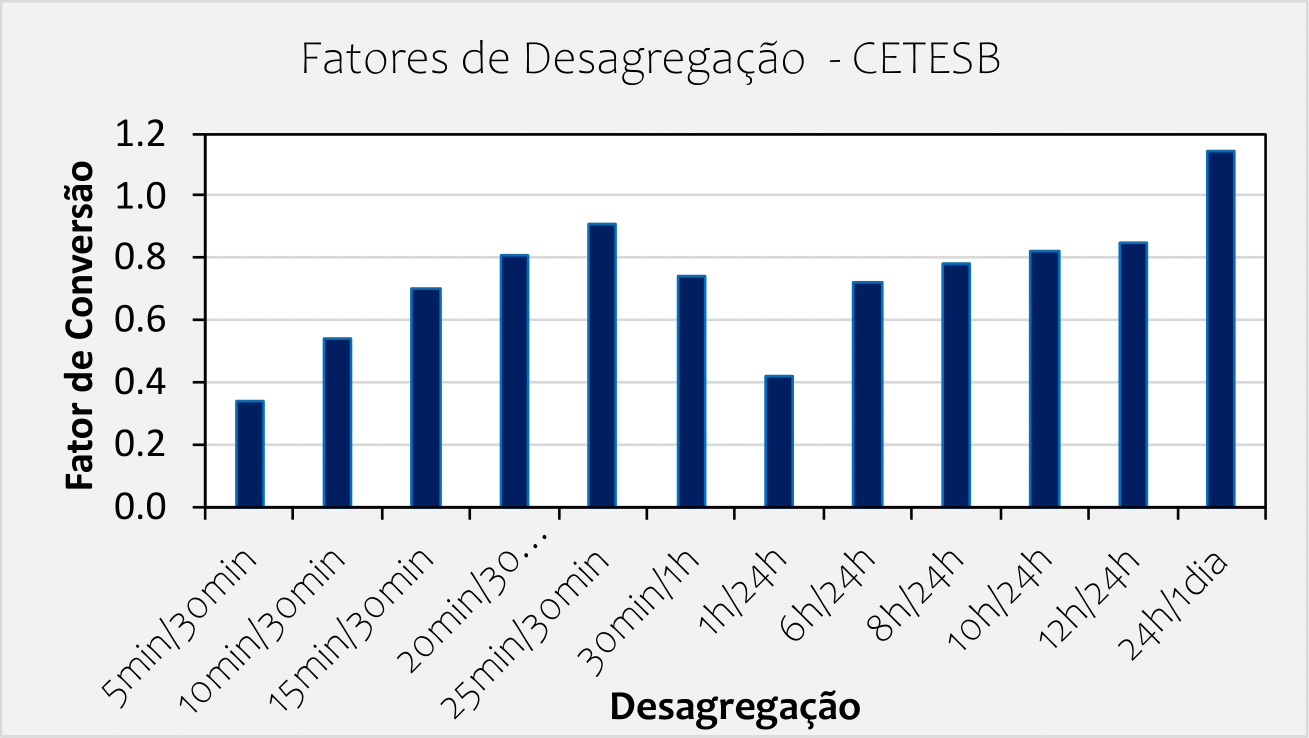
Os valores do gráfico acima são apresentados na tabela abaixo:
| Relação | 5min/30min | 10min/30min | 15min/30min | 20min/30min | 25min/30min | 30min/1h | 1h/24h | 6h/24h | 8h/24h | 10h/24h | 12h/24h | 24h/1dia |
| Coef. Desagregação | 0.34 | 0.54 | 0.7 | 0.81 | 0.91 | 0.74 | 0.42 | 0.72 | 0.78 | 0.82 | 0.85 | 1.14 |
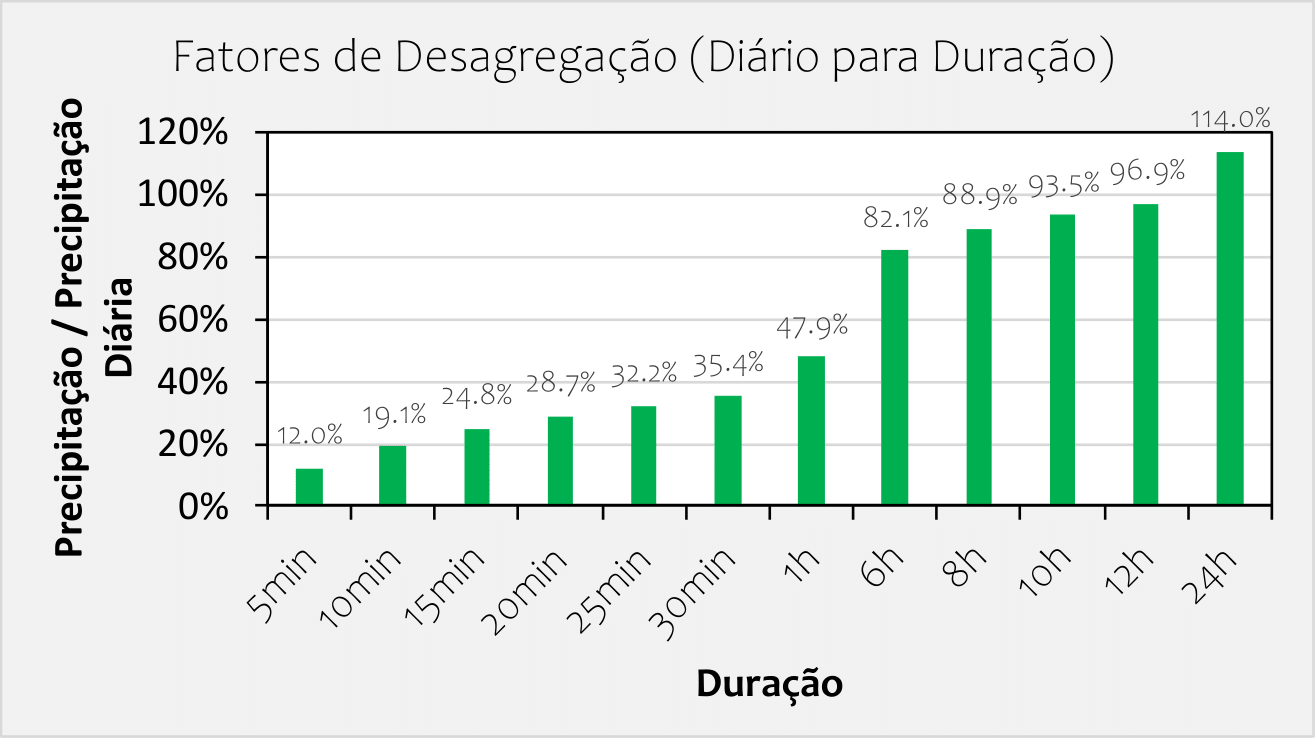
Diferença de Chuva Diária e Chuva de 24h
Nota-se algo interessante da figura anterior.
Você pode se perguntar: qual a diferença de uma chuva diária e de uma chuva de 24h? E qual a razão da chuva de 24h ser 114% da chuva diária?
Se pararmos para analisar, valores medidos por pluviômetros são valos acumulados em 24 h.
Porém, as medidas desses pluviômetros são sempre tomadas em um horário específico do dia (e.g., todo dia as 10h de manhã, por exemplo).
Acontece que muitas vezes a chuva de 24h com maior volume não ocorrerá de fato entre as 10h de um dia e as 10h do outro.
Para considerar esse efeito, um fator de 14% a mais serve de parâmetro para compensar esse efeito.
Aliás, esse parâmetro foi obtido experimentalmente via medições de volume de chuva em alta resolução temporal em pluviômetros.
Geralmente esses dados são a cada 5 ou 15 minutos, o que permite estimar os coeficientes de desagregação de uma maneira mais realista.
Essa seria a razão de se converter de uma chuva diária para uma chuva de 24 h e obter um valor 14% maior.
Exemplo 1)
Dado uma chuva diária de 200 mm com TR = 100 anos, determine o valor da chuva de 15-min e mesmo tempo de retorno usando os coeficientes de desagregação da CETESB.
Solução:
Basta usar o coeficiente de conversão de chuva diária para chuva de 15 minutos, isto é, pela figura anterior, este coeficiente é 24.8%.
Assim, a precipitação de 200 anos, mas com duração de 24.8% é $P = 0.248*200 = 49~\mathrm{mm}$
Exemplo 2)
Determine todas as chuvas sub-diárias para as durações fornecidas nos coeficientes de desagregação da CETESB para uma chuva com tempo de retorno de 100 anos, ajustada pelo método Gumbel para a seguinte série de precipitação $\mathbf{P} = [100,~120,~200,~150,~160,~175,~155,~170,~165,~190,~175,~200]^T$
Solução:
Usando o método desenvolvido no artigo da distribuição de Gumbel, (se você não viu, clique aqui), chegamos na expressão que relaciona o tempo de retorno e valor da variável aleatória em função da média e desvio padrão da amostra, de modo que:
$$P(\mathrm{1~dia},TR) = \bar{P} + s(0.45 + 0.779 \mathrm{ln}\Bigl(\mathrm{ln}(\frac{\mathrm{TR}}{\mathrm{TR}-1})\Bigr)$$
$$P(\mathrm{1~dia},TR) =163.33 + 29.9(0.45 + 0.779 \mathrm{ln}\Bigl(\mathrm{ln}(\frac{\mathrm{TR}}{\mathrm{TR}-1})\Bigr)$$
Se aplicarmos a equação anterior para TR = 100 anos, obtemos:
$$P(\mathrm{1~dia},100) =163.33 + 29.9(0.45 + 0.779 \mathrm{ln}\Bigl(\mathrm{ln}(\frac{\mathrm{100}}{\mathrm{100}-1})\Bigr)$$
$$P(\mathrm{1~dia},100) = 257.3~\mathrm{mm}$$
Agora, de posse da chuva de diária, basta desagregarmos para cada um dos coeficientes da CETESB, resultando em:
| Duração (min) | Duração (hora) | Dia / Duração | P(t) | i(t) |
| 5 | 0.08 | 0.12 | 31.0 | 371.9 |
| 10 | 0.17 | 0.19 | 49.2 | 295.3 |
| 15 | 0.25 | 0.25 | 63.8 | 255.2 |
| 20 | 0.33 | 0.29 | 73.8 | 221.5 |
| 25 | 0.42 | 0.32 | 83.0 | 199.1 |
| 30 | 0.50 | 0.35 | 91.2 | 182.3 |
| 60 | 1.00 | 0.48 | 123.2 | 123.2 |
| 360 | 6.00 | 0.82 | 211.2 | 35.2 |
| 480 | 8.00 | 0.89 | 228.8 | 28.6 |
| 600 | 10.00 | 0.93 | 240.5 | 24.1 |
| 720 | 12.00 | 0.97 | 249.3 | 20.8 |
| 1440 | 24.00 | 1.14 | 293.3 | 12.2 |

Mestre e Doutor em Engenharia Hidráulica e Saneamento pela USP – São Carlos. Vencedor do Prêmio Tese Destaque de teses da USP (2024) e autor de diversos artigos nacionais e artigos internacionais. Pesquisador de Pós-Doutorado II na University of Arizona, Department of Hydrology and Atmospheric Sciences, USA. Engenheiro civil formado pela Universidade Estadual de Maringá. Fundou o canal Engenheiro Planilheiro em 2017 após perceber que suas planilhas poderiam dar uma contribuição real para diversos engenheiros, arquitetos e profissionais da área, contando com mais de 100 mil planilhas já baixadas e diversos clientes atendidos no Brasil e no mundo.


2 respostas
Excelente
Legal Rita, temos também um curso completo de Hidrologia Estatística com 8h envolvendo desde os princípios básicos de chuvas extremas até a elaboração de curvas IDF. Entre em contato para mais informações!