Balanço de Energia (1): fluxos de superfície, leis de radiação e radiação líquida
Este artigo apresenta conceitos básicos para modelar vapor d’água: o que é fluxo na superfície, como energia vira evaporação, as leis de radiação e como calcular a radiação líquida.
1) Conceito, contextualização e importância
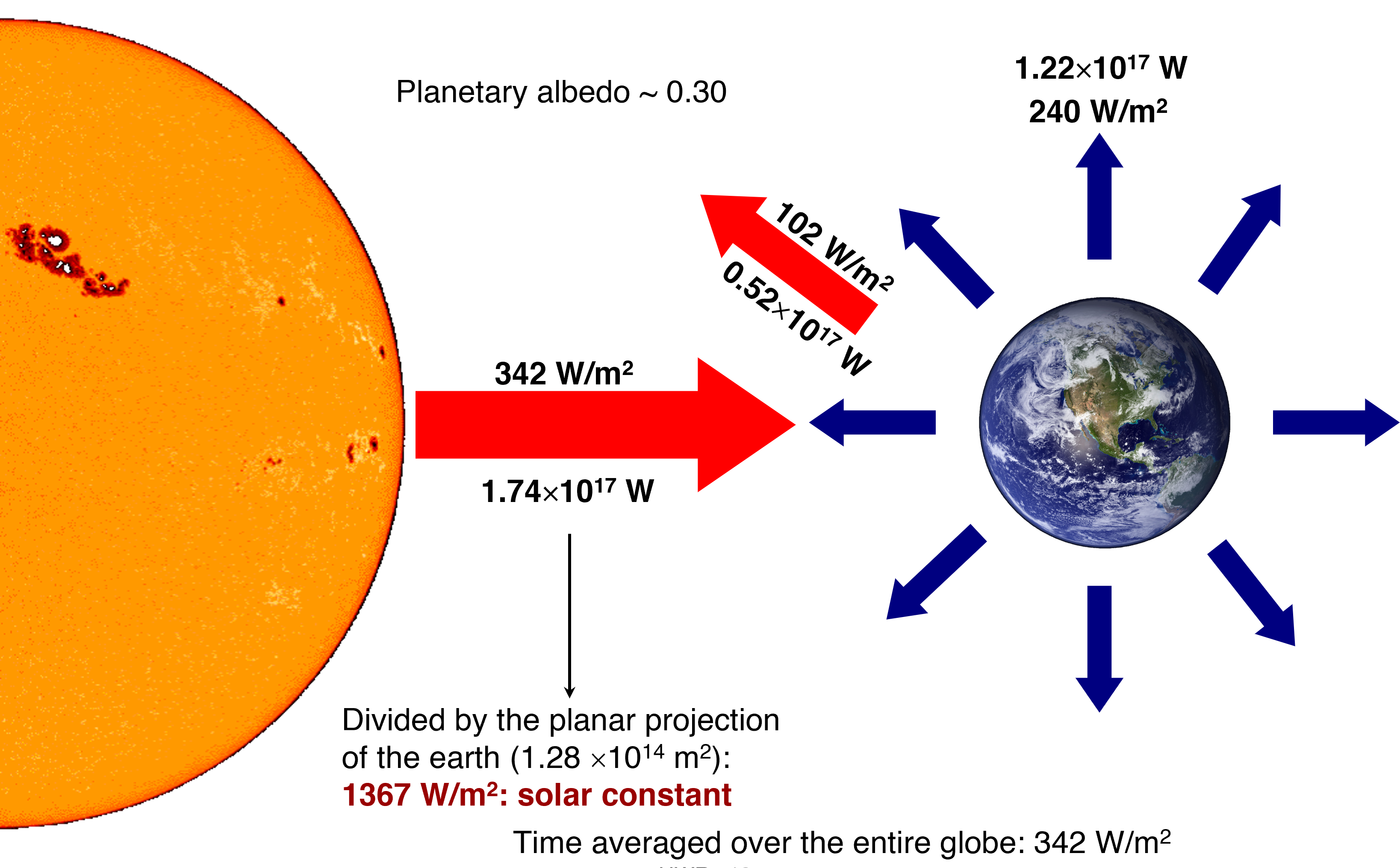
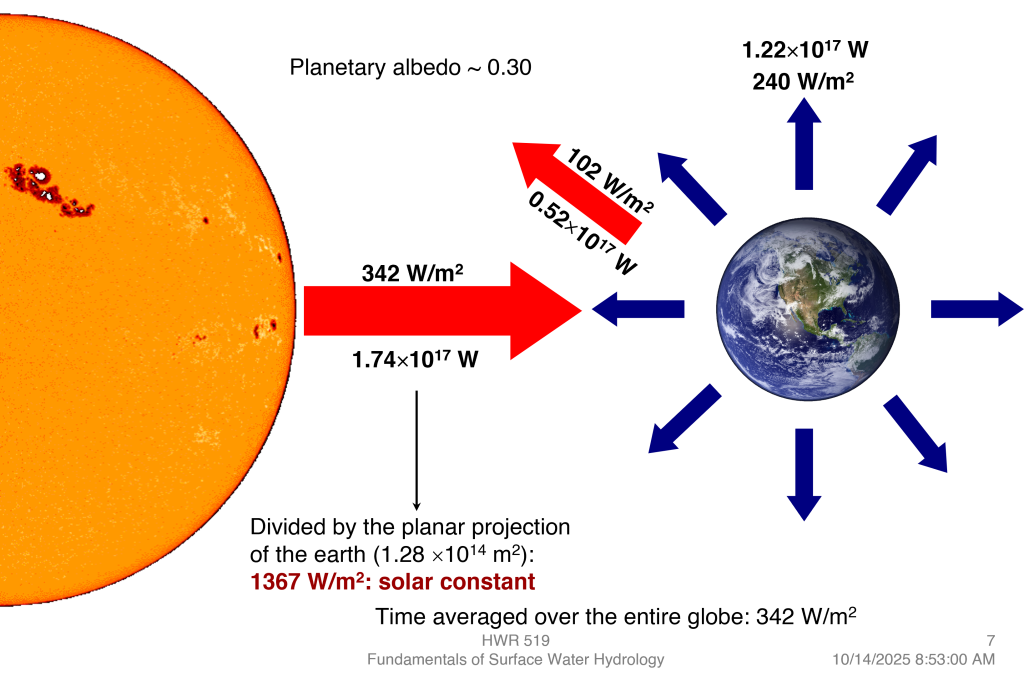
A energia solar é o motor do ciclo hidrológico. Ela aquece a superfície, move o vapor d’água e sustenta a evaporação e a evapotranspiração.
Três perguntas guiam o estudo: Quanto de radiação a Terra recebe por dia? Como se distribui ao longo do ano? O que controla essa variabilidade?
2) Fluxos de superfície (definição e unidades)
2.1. Definição de fluxo
Fluxo é a quantidade que atravessa uma área unitária por unidade de tempo, na direção considerada.
Fluxo é, portanto, perpendicular à área de superfície.
2.2. Principais fluxos superficiais
- Fluxo de evaporação, $E$ — fluxo de massa de água [kg m-2 s-1].
- Fluxo de calor latente — energia associada à evaporação: $\lambda E$ [W m-2], com $\lambda$ o calor latente de vaporização.
- Fluxo de calor sensível, $H$ — fluxo de calor por gradiente térmico [W m-2].
- Fluxo de radiação solar, $S_r$ — fluxo de radiação [W m-2].
Conversão útil: 1 mm dia-1 ≈ 28,6 W m-2 (≈ 30 W m-2).
3) Formulação matemática
3.1. Fluxo de calor latente
$$
Q_\mathrm{lat} = \lambda E
$$
- $Q_\mathrm{lat}$ — fluxo de calor latente [W m-2].
- $\lambda$ — calor latente de vaporização [J kg-1] (use $\lambda \approx 2{,}454\times10^{6}$ J kg-1).
- $E$ — fluxo de evaporação [kg m-2 s-1].
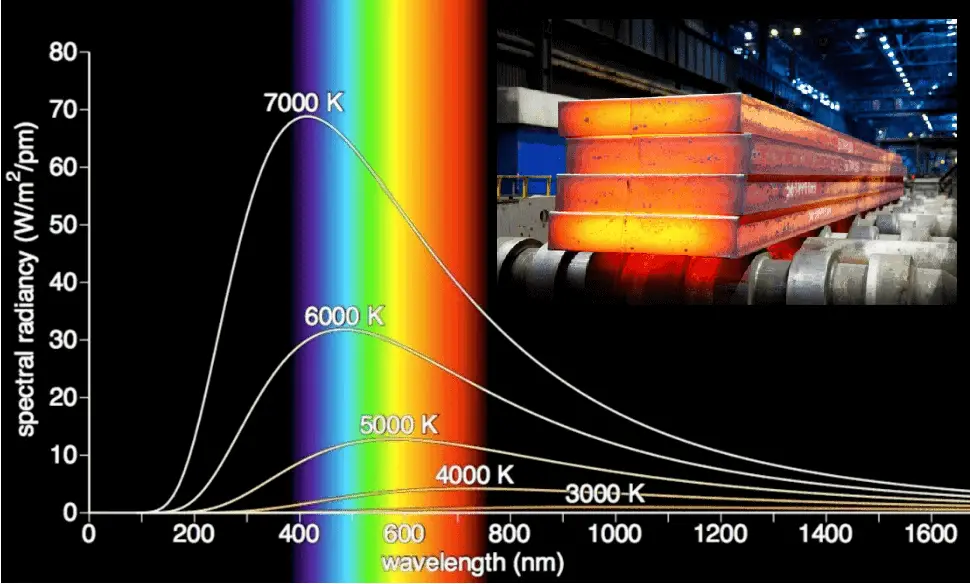
3.2. Lei de Stefan–Boltzmann (corpo negro)
$$
R = \sigma T^{4}
$$
- $R$ — fluxo radiativo emitido por unidade de área [W m-2].
- $\sigma = 5{,}67\times10^{-8}$ W m-2 K-4 — constante de Stefan–Boltzmann.
- $T$ — temperatura absoluta [K].
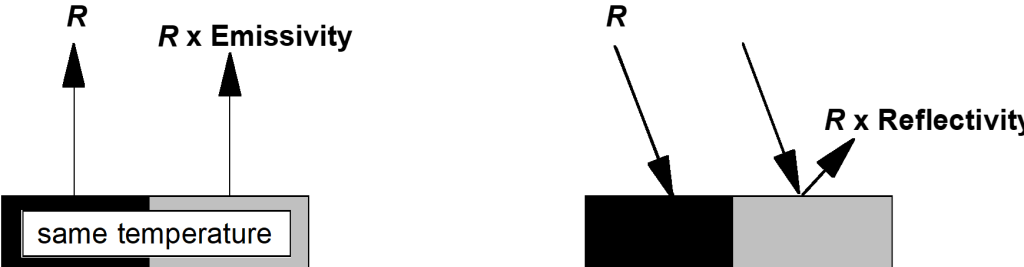
3.3. Superfícies “cinza”: albedo e emissividade
Albedo ($\alpha$): fração da radiação solar de onda curta refletida pela superfície (≈ 0,15–0,25 para vegetação verde, até 0,80–0,90 para neve fresca).
Emissividade ($\varepsilon$): razão entre a radiação emitida pela superfície e a de um corpo negro à mesma temperatura (superfícies naturais: 0,95–0,99).
3.4. Radiação líquida na superfície
$$
R_n = R_s\,(1-\alpha_s) + \varepsilon_s\,R_{ld} – R_{lu}
$$
- $R_n$ — radiação líquida [W m-2].
- $R_s$ — radiação solar de onda curta incidente [W m-2].
- $\alpha_s$ — albedo da superfície [–].
- $R_{ld}$ — radiação atmosférica descendente (onda longa) [W m-2].
- $R_{lu}$ — radiação de onda longa emitida pela superfície [W m-2].
- $\varepsilon_s$ — emissividade da superfície [–].
Observações práticas: $R_n$ pode ser medido por radiômetros líquidos; para maior precisão, estime cada componente separadamente.
4) Exemplo prático — conversão energia–água (Lago Tana)
Dados: evaporação anual $E_\mathrm{anual}=1{,}5$ m ano-1; densidade da água $\rho_w=1000$ kg m-3; calor latente $\lambda=2{,}454\times10^{6}$ J kg-1; radiação solar média incidente $R_s=325$ W m-2.
Passo 1 — fluxo de massa (converter m ano-1 para kg m-2 s-1):
$$
E = \frac{\rho_w \, E_\mathrm{anual}}{365 \times 24 \times 60 \times 60}
= \frac{1000 \times 1{,}5}{31{,}536{,}000}
\;\approx\; 4{,}76\times10^{-5}\ \mathrm{kg\,m^{-2}\,s^{-1}}
$$
Passo 2 — fluxo de energia (calor latente):
$$
Q_\mathrm{lat} = \lambda E
= 2{,}454\times10^{6} \times 4{,}76\times10^{-5}
\;\approx\; 1{,}17\times10^{2}\ \mathrm{W\,m^{-2}}
$$
Passo 3 — balanço de energia (proporção da radiação que “vira” evaporação):
$$
\frac{Q_\mathrm{lat}}{R_s} \approx \frac{117}{325} \approx 0{,}36 \;\; (\text{36%})
$$
O restante vai para reflexão (albedo), aquecimento do ar (calor sensível), aquecimento do solo/água e emissão de onda longa.
Dica: insira aqui a lâmina “Energy–water conversion (Lake Tana)”.
5) Tabelas úteis (ordem de grandeza)
5.1. Albedo de superfícies naturais
| Superfície | Albedo (–) |
|---|---|
| Água profunda | 0,04 – 0,08 |
| Solo escuro úmido | 0,05 – 0,15 |
| Vegetação herbácea verde | 0,15 – 0,25 |
| Grama seca / restolho | 0,15 – 0,20 |
| Floresta de coníferas | 0,10 – 0,15 |
| Floresta decídua | 0,15 – 0,25 |
| Neve (recente) | 0,80 – 0,90 |
5.2. Emissividade de superfícies naturais
| Superfície | Emissividade (–) |
|---|---|
| Solo exposto (mineral) | 0,95 – 0,97 |
| Solo exposto (orgânico) | 0,97 – 0,98 |
| Vegetação herbácea | 0,97 – 0,98 |
| Vegetação arbórea | 0,96 – 0,97 |
| Neve (antiga) | 0,97 |
| Neve (recente) | 0,99 |
6) Incertezas e por que importam
- Medição: calibração e resposta espectral de radiômetros; estimativa de $\alpha$ e $\varepsilon$.
- Variabilidade: heterogeneidade de superfície; sazonalidade.
- Parâmetros: $\lambda$ varia com a temperatura; escolha de $\varepsilon$ e $\alpha$ influencia $R_n$ e, portanto, $E$.
7) Conclusões e observações
Fluxos de superfície conectam energia e água. O calor latente traduz evaporação em watts por metro quadrado. A radiação líquida depende de albedo, emissividade e das componentes de onda curta e longa. Esses conceitos sustentam a modelagem de vapor d’água e a estimativa de E/ET.


Mestre e Doutor em Engenharia Hidráulica e Saneamento pela USP – São Carlos. Vencedor do Prêmio Tese Destaque de teses da USP (2024) e autor de diversos artigos nacionais e artigos internacionais. Pesquisador de Pós-Doutorado II na University of Arizona, Department of Hydrology and Atmospheric Sciences, USA. Engenheiro civil formado pela Universidade Estadual de Maringá. Fundou o canal Engenheiro Planilheiro em 2017 após perceber que suas planilhas poderiam dar uma contribuição real para diversos engenheiros, arquitetos e profissionais da área, contando com mais de 100 mil planilhas já baixadas e diversos clientes atendidos no Brasil e no mundo.