Ciclo da Água e Energia no Planeta “Água”
A Terra é o “planeta água”. Mas quase toda a água é salgada. A água doce é pouca. E apenas uma fração mínima está acessível.
Por que isso importa? Porque a gestão hídrica depende de onde a água está (estoques) e como ela circula (fluxos e energia). Sem essa visão, subestimamos o risco de escassez.
Outra perspectiva: quanta água realmente temos?
- Se toda a água do planeta fosse reunida, formaria uma esfera com diâmetro de ~860 milhas (~1.384 km).
- Apenas ~2,5% é água doce.
- Cerca de ~69% da água doce está em geleiras, snow pack permanente e permafrost.
- ~30% está em aquíferos.
- ~1% da água doce é superficial (lagos e rios).
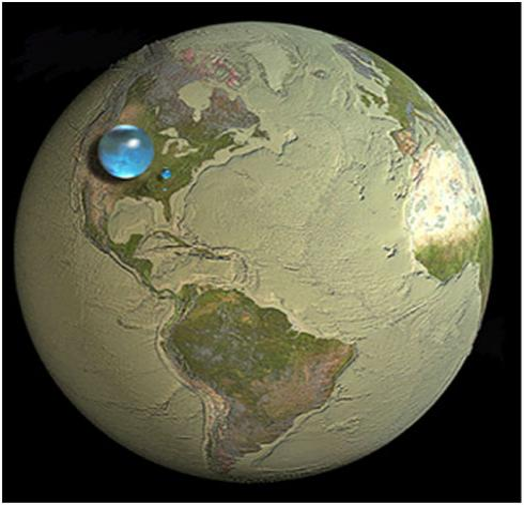
Globe illustration by Jack Cook (©); Adam Nieman)
Equação da esfera equivalente
$$
R = \left(\frac{3V}{4\pi}\right)^{1/3} \quad \text{e} \quad D = 2R
$$
onde:
- $V$ é o volume total de água [ L3 ].
- $R$ é o raio equivalente [ L ].
- $D$ é o diâmetro equivalente [ L ].
Nosso consumo de água e seu impacto no ciclo da água e energia
- Domicílios: ~80 galões por pessoa por dia.
- Consumo total nos EUA: ~2000 galões per capita por dia (pegada hídrica total: alimentos, energia e bens).
- 1 kg de carne bovina: ~4000 galões para produzir.
- A alfafa lidera o consumo de água na Califórnia.
- A Califórnia exporta ~100 bilhões de galões de água por ano (água “virtual” nos produtos).

Balanço hídrico global (volumes e lâminas)
Valores médios anuais (ordem de grandeza) e conversão para lâmina:
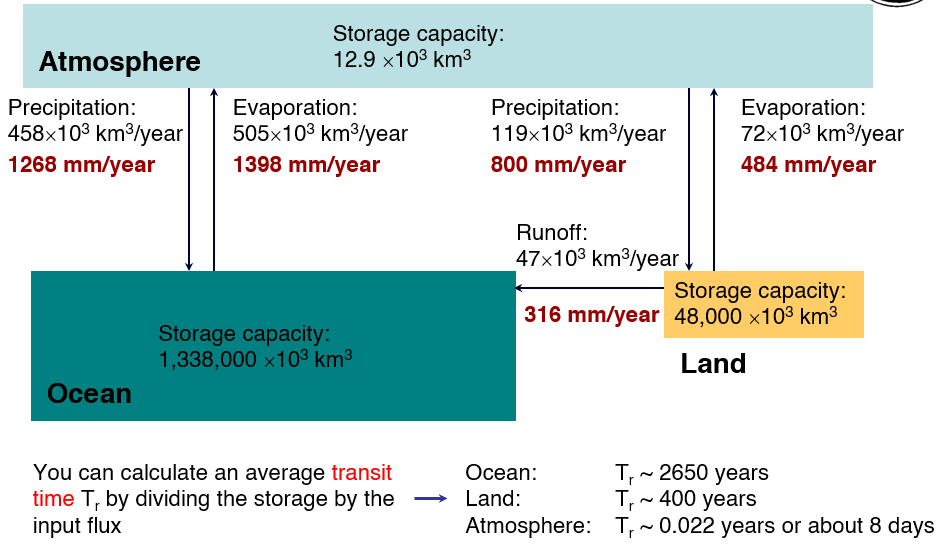
- Atmosfera: capacidade de armazenamento ≈ 12,9 × 103 km³.
- Oceano: armazenamento ≈ 1.338.000 × 103 km³; área $A_\mathrm{oce}$ ≈ 3,61 × 1014 m².
- Continentes: armazenamento ≈ 48.000 × 103 km³; área $A_\mathrm{terr}$ ≈ 1,49 × 1014 m².
Fluxos anuais típicos e suas lâminas:
- Oceano — Evaporação: 505 × 103 km³/ano → 1398 mm/ano; Precipitação: 458 × 103 km³/ano → 1268 mm/ano.
- Continentes — Precipitação: 119 × 103 km³/ano → 800 mm/ano; Evaporação: 72 × 103 km³/ano → 484 mm/ano; Escoamento: 47 × 103 km³/ano → 316 mm/ano.
Como converter km³/ano para mm/ano?
$$
h\;[\mathrm{mm/ano}] \;=\; \frac{V\;[\mathrm{km^3/ano}]\;\times\;10^{12}\;[\mathrm{m^3/km^3}]}{A\;[\mathrm{m^2}]}\;\times\;1000\;[\mathrm{mm/m}]
$$
onde:
- $V$ é o volume anual escoado/precipitado/evaporado.
- $A$ é a área do compartimento (oceano ou terra).
- $h$ é a lâmina média anual equivalente.
Tempo de residência (ou trânsito)
Por definição, é o tempo médio em que um determinado volume de controle tem seu estoque totalmente preenchido.
$$
T_r = \frac{S}{F}
$$
- Oceano: $T_r \sim 2650$ anos.
- Continentes (terras emersas): $T_r \sim 400$ anos.
- Atmosfera: $T_r \sim 0{,}022$ ano ≈ 8 dias.
Aqui percebe-se a dificuldade de se fazer previsões de chuva ou de variáveis atmosféricas de longo prazo.
Em apenas 8 dias, toda a umidade da atmosfera se renova, o que torna o processo de previsão extremamente dependente de condições iniciais e, de certo modo, caótico.
Balanço global de energia (ponte para o vapor d’água)
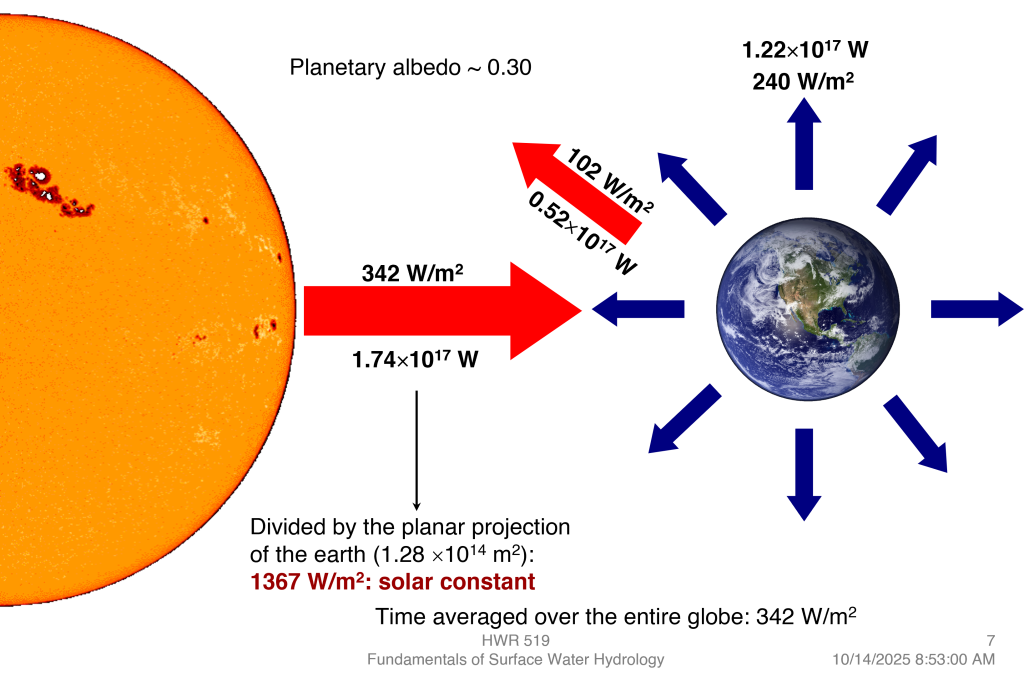
- Constante solar (no topo da atmosfera): ~1367 W/m².
- Média global sobre a superfície (distribuída na esfera): ~342 W/m².
- Albedo planetário ≈ 0,30 → reflexão de ~102 W/m².
- Saída média por radiação de onda longa para o espaço: ~240 W/m².
Ideia-chave
A energia solar disponível controla a evaporação (fluxo de vapor). Ao longo da série de artigos que estamos escrevendo, vamos ligar o balanço de energia à modelagem de vapor d’água e à evapotranspiração potencial.
Exemplos práticos
Exemplo A — diâmetro da esfera de “toda a água”
Dados: $V = 1{,}386\times10^{9}\ \mathrm{km^3}$.
$$
R=\left(\frac{3\times 1{,}386\times10^{9}}{4\pi}\right)^{1/3}\ \mathrm{km}, \qquad D=2R
$$
Resultado: $D \approx 1{,}384\ \mathrm{km}$ (≈ 860 milhas).
Exemplo B — tempo de residência da atmosfera
Dados: $S = 12{,}900\ \mathrm{km^3}$; $F = 505{,}000\ \mathrm{km^3/ano}$.
$$
T_r=\frac{S}{F}=\frac{12{,}900}{505{,}000}=0{,}0255\ \mathrm{ano}\;\approx\;9{,}3\ \mathrm{dias}
$$
Exemplo C — conferindo a lâmina de 1398 mm/ano (evaporação do oceano)
Dados: $V=505\times10^{3}\ \mathrm{km^3/ano}$; $A_\mathrm{oce}=3{,}61\times10^{14}\ \mathrm{m^2}$.
$$
h=\frac{505\times10^{3}\times 10^{12}}{3{,}61\times10^{14}}\times 1000 \;\approx\; 1398\ \mathrm{mm/ano}
$$
Incertezas que importam
- Medição e método: sensores, satélites, estimativas de estoques e fluxos.
- Escalas: médias globais escondem extremos regionais e sazonais; séries curtas aumentam a incerteza.
- Conversões e hipóteses: arredondamentos (km³ ↔ mm/ano) e modelos de “caixa única”.
- Impacto prático: disponibilidade hídrica, comunicação de risco e planejamento de infraestrutura.
Conclusões e observações
“Planeta água” não significa água doce abundante. A fração acessível é pequena. Estoques grandes não garantem disponibilidade local.
O tempo de residência explica respostas rápidas (atmosfera), intermediárias (continentes) e lentas (oceanos). A energia solar governa a evaporação e, portanto, a dinâmica do vapor d’água.
Próximo artigo: Balanço de Energia (1) — radiação, albedo, emissividade e a ligação direta com a evaporação.
O conteúdo desta série de artigos é baseados nas notas de aula do prof. Peter A. Troch, da Universidade do Arizona, Departamento de Hidrologia e Ciências Atmosphericas.

Mestre e Doutor em Engenharia Hidráulica e Saneamento pela USP – São Carlos. Vencedor do Prêmio Tese Destaque de teses da USP (2024) e autor de diversos artigos nacionais e artigos internacionais. Pesquisador de Pós-Doutorado II na University of Arizona, Department of Hydrology and Atmospheric Sciences, USA. Engenheiro civil formado pela Universidade Estadual de Maringá. Fundou o canal Engenheiro Planilheiro em 2017 após perceber que suas planilhas poderiam dar uma contribuição real para diversos engenheiros, arquitetos e profissionais da área, contando com mais de 100 mil planilhas já baixadas e diversos clientes atendidos no Brasil e no mundo.

