Evaporação ao Nível de Parcela: da similaridade turbulenta ao modelo de Penman–Priestley-Taylor

É fim da manhã na parcela. O Sol já entregou energia, a superfície aqueceu e a camada de ar logo acima ficou turbulenta. Para saber quanto vapor sobe, precisamos de três ideias simples: (1) energia disponível na superfície; (2) gradientes de temperatura/umidade no ar próximo; (3) turbulência que “conecta” a superfície ao ar. Com isso, chegamos aos métodos clássicos de campo.

 

---

1) Similaridade turbulenta: por que gradiente → fluxo

Na ASL, a turbulência mistura ar em “redemoinhos”. A hipótese de similaridade diz que um fluxo turbulento é proporcional a um gradiente médio da grandeza transportada. Isso leva às formas “bulk” (duas alturas) ou “perfil” (uma altura + perfis logarítmicos).

1.1. Forma bulk (duas alturas)

$$
\overline{w’ q’} \;=\; -\,C_e\,(u_2-u_1)\,(q_2-q_1)
$$

Usando o valor à superfície ($q_s$) e uma altura $z_1$ acima d’água/vegetação, a evaporação específica fica:

$$
E \;=\; C_e\,\rho\,u_1\,(q_s – q_1)
$$

• $E$ [kg m^-2 s^-1], $\rho$ densidade do ar, $u$ velocidade do vento, $q$ umidade específica.
• Sobre água, $q_s$ é saturado à $T_s$. Sobre dossel, usa-se parametrizações (mais incertas).

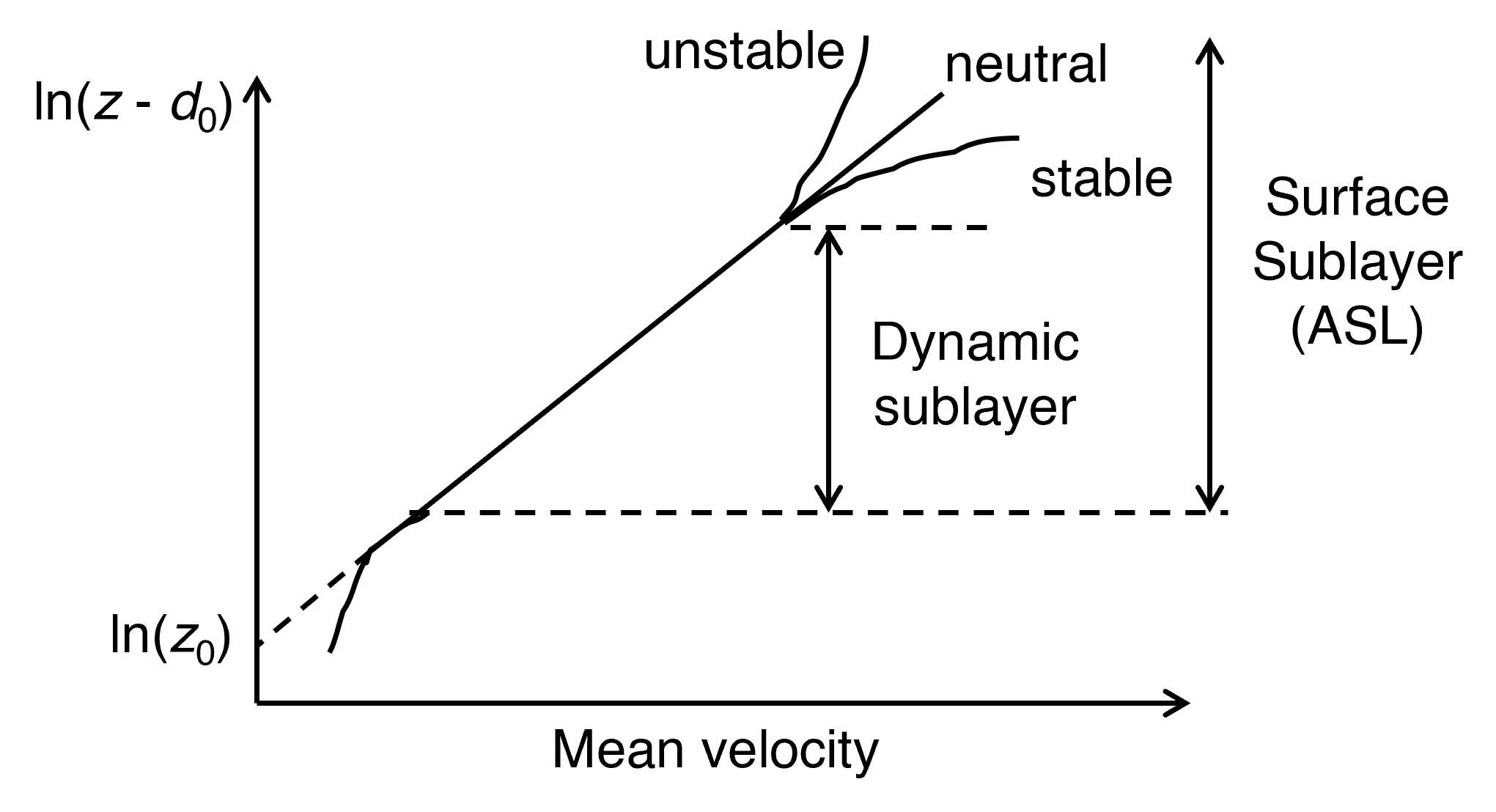
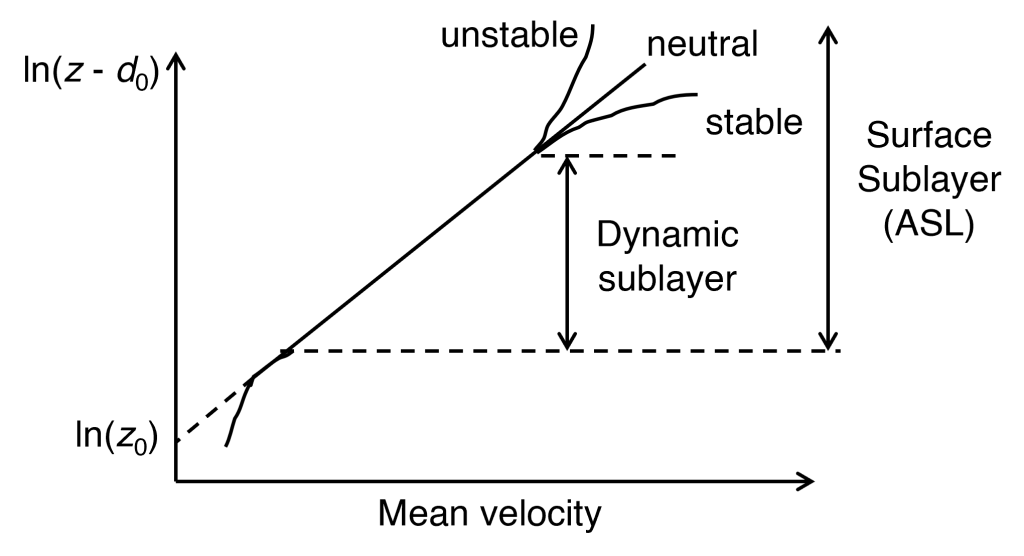
1.2. Perfil logarítmico (uma altura) e coeficiente de troca

Sob condições neutras e superfície homogênea:

$$
u(z) \;=\; \frac{u_*}{k}\,\ln\!\frac{z-d_0}{z_0},
\qquad
C_e \;\approx\; \left[\frac{k}{\ln\!\big((z_1-d_0)/z_0\big)}\right]^2
$$

• $k\!\approx\!0{,}4$ (von Kármán); $z_0$ roughness length; $d_0$ zero-plane displacement (vegetação).
• Quanto mais rugosa a superfície, maior $z_0$ e maior a troca.

---

2) Fechamento energético com razão de Bowen (EBBR)

No saldo de energia diário/horário, a superfície reparte a radiação líquida em latente, sensível e solo/água:

$$
R_n \;=\; \lambda E \;+\; H \;+\; G
$$

A razão de Bowen contorna a falta de medição direta de $E$ e $H$ a partir de perfis de $T$ e $q$:

$$
\mathrm{Bo} \;=\; \frac{H}{\lambda E}
\;\;\;\Rightarrow\;\;\;
\lambda E \;=\; \frac{R_n – G}{1+\mathrm{Bo}},
\qquad
H \;=\; \mathrm{Bo}\,\lambda E
$$

Estimativa prática de Bo com dados de duas alturas (médias de 15–30 min):

$$
\mathrm{Bo} \;\approx\; \gamma\,
\frac{\Delta T}{\Delta e}
\qquad
\text{com}\;\;
\gamma \ \text{(psicrométrica)}\;,\;
\Delta e = e_2 – e_1
$$

Atenção: singularidade em $\mathrm{Bo}\approx -1$ (manhã cedo/anoitecer, $H\!\approx\!0$). Evitar esses períodos.

---

3) Penman para superfícies molhadas

Com superfície molhada ($q_s \approx q^*(T_s)$) e advecção moderada, Penman combina energia e aerodinâmica:

$$
\lambda E \;=\;
\underbrace{\frac{\Delta}{\Delta+\gamma}\,Q_{ne}}_{\text{termo de energia}}
\;+\;
\underbrace{\frac{\gamma}{\Delta+\gamma}\,E_A}_{\text{termo aerodinâmico}}
$$

$$
Q_{ne} = R_n – G,
\qquad
E_A \;\propto\; \rho\,c_p\,f(u)\,\big(e_s^*(T_a)-e_a\big)
$$

• $\Delta$ inclinação da curva de saturação; $\gamma$ psicrométrica; $f(u)$ função do vento.
• Interpretação: parte de energia + parte do “poder de secagem” do ar.

4) Priestley–Taylor: quando a advecção é pequena

Sobre extensas áreas úmidas (oceano/irrigado), a advecção local tende a ser pequena e Penman simplifica:

$$
\lambda E \;=\; \alpha_e\,\frac{\Delta}{\Delta+\gamma}\,Q_{ne},
\qquad
\alpha_e \approx 1{,}26
$$

• Ajuste empírico: $\alpha_e\sim 1{,}2$–$1{,}3$ para “quase equilíbrio”.
• Útil como limite inferior em superfícies muito úmidas (sem advecção local forte).

---

5) Medindo na prática: três rotas rápidas

1. Bulk/profile — requer $u$, $q$ (e às vezes $T$) em 1–2 alturas e parâmetros de rugosidade ($z_0$, $d_0$). Funciona muito bem sobre água; sobre vegetação precisa de cuidados com $q_s$ e estabilidade.
2. EBBR — usa $R_n$, $G$, perfis de $T$ e $q$. Evitar janelas com $H\!\approx\!0$ e checar estacionariedade de 15–30 min.
3. Penman / P–T — requer $R_n$ (ou radiação curta/longa), $T_a$, $e_a$, vento. Penman capta advecção; P–T é “potencial úmido” com advecção mínima.

---

6) Receita mínima (com unidades) para a operação

6.1. Termos termodinâmicos

$$
e^*(T) = 0{,}6108\,\exp\!\left(\frac{17{,}27\,T}{T+237{,}3}\right)\ \ [\mathrm{kPa}],
\qquad
\Delta(T) = \frac{4098\,e^*(T)}{(T+237{,}3)^2}\ \ [\mathrm{kPa\ ^\circ C^{-1}}]
$$

$$
\gamma \approx 0{,}066\ \mathrm{kPa\ ^\circ C^{-1}}\ \text{(nível do mar)},
\qquad
\lambda \approx 2{,}454\times10^6\ \mathrm{J\,kg^{-1}}
$$

6.2. Fechamento escolhido

• EBBR: $\displaystyle \lambda E=\frac{R_n-G}{1+\mathrm{Bo}}$ com $\mathrm{Bo}\approx\gamma\,\Delta T/\Delta e$.
• Penman: $\displaystyle \lambda E=\frac{\Delta}{\Delta+\gamma}Q_{ne}+\frac{\gamma}{\Delta+\gamma}E_A$.
• P–T: $\displaystyle \lambda E=\alpha_e\frac{\Delta}{\Delta+\gamma}Q_{ne}$ com $\alpha_e\!\approx\!1{,}26$.

---

7) O que realmente importa (e dá erro)

• Energia: $R_n$ e $G$ bem medidos são meia-solução. Sombra/tilt do radiômetro e calor no solo dominam o erro.
• Rugosidade e estabilidade: $z_0$, $d_0$ e condição (neutra/estável/instável) mudam os coeficientes de troca.
• Advecção: se o ar chega mais seco/quente, Penman “ganha” do P–T. Em fetch curto, EBBR pode falhar na suposição 1-D.
• Janelas ruins: $\mathrm{Bo}\approx -1$ (alvorada/crepúsculo) e períodos não-estacionários distorcem o balanço.

---