Amortecimento de Cheias em Reservatórios

Métodos, modelos, equações e exemplos

1 – Introdução

O amortecimento de cheias em reservatórios é um processo de cálculo que, se feito de maneira metódica, é relativamente simples e prático.

Nesse artigo vamos aprender a base de como realizar um bom projeto de amortecimento de cheias em reservatórios e entender a razão do método PULS ser utilizado com frequência em projetos hidráulicos de reservatórios

2 – Formulação Matemática – Métodos de Amortecimento de Cheias em Reservatórios 

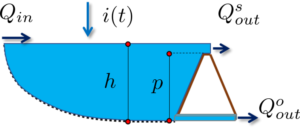
Imagine que temos um reservatório com curva cota-área conhecida, de modo que sabemos uma relação unívoca entre a área do reservatório e sua altura.

O balanço de massa em um reservatório é semelhante ao fluxo de caixa em uma conta corrente.

Em linhas gerais, a diferença entre o que entra e saí em um reservatório é justamente o que se tem armazenado nele, de modo que:

$$
\frac{\mathrm{d}S(t)}{\mathrm{d}t} = Q_{in}(t)~-~Q_{out}(t) \label{equ:mass_balance} \tag{1}
$$

Onde $Q_{in}$ é a vazão que entra no reservatório (e.g., geralmente proveniente do hidrograma de entrada resultante do estudo hidrológico), $Q_{out}$ é a vazão de saída do reservatório e $S(t)$ é o seu volume armazenado.

Percebe-se que todas as variáveis estão indexadas no instante t, indicando que variam ao longo do tempo.

A equação diferencial apresentada anteriormente parece relativamente simples se conhecermos funções que descrevem $Q_{in}(t)$ e $Q_{out}(t)$.

Em relação a vazão de entrada, até conhecemos uma forma de estimar seu resultado de forma discretizada, mas dificilmente temos uma equação contínua e analítica que explique $Q_{in}(t)$ muito pelo fato de que modelos hidrológicos geralmente são bem não lineares.

Por outro lado, temos sim uma equação contínua e diferenciável que define e modela a vazão de saída do reservatório com base na conservação da energia, mas ela não é suficiente para salvar nossa vida de uma matemática um poquinho mais intensa.

Vamos ve-la logo a seguir.

2.1 – Conservação de Massa e de Energia em Reservatórios

Aplicando-se a conservação da energia entre um ponto localizado no espelho d’água do reservatório e outro localizado logo na saída que descarrega em pressão atmosférica, temos que:

$$
\frac{P_1}{\gamma}+ \frac{v_1^2}{2g} + z1 = \frac{P_2}{\gamma} + \frac{v_2^2}{2g} + z_2 + \Delta h_{1,2} \tag{2}
$$

Onde $P$ é a pressão manométrica, $v$ a velocidade média do escoamento, $\gamma$ é o peso específico da água (densidade x gravidade) e $z$ a elevação do ponto em relação a um referencial.

Desprezando-se $v_1$, $P_1$ e $P_2$ e incluindo os efeitos da perda de carga entre os pontos $\Delta h_{1,2}$ em um coeficiente chamado de coeficiente de descarga $C_d$, temos que:

$$
v = C_d\sqrt{2g(z_1 – z_2)} \tag{3}
$$

Além disso, se quisermos transformar a equação anterior em vazão, basta multiplicarmos pela área do orifício, o que resulta em:

$$
Q_{out}^o = C_d.A_{ef}.\sqrt{2g(z_1 – z_2)} \tag{4}
$$

Onde $Q_{out}^o$ é a vazão que saí do orifício, em função do desnível $h = z_1 – z_2$ e $A_{ef}$ é a área efetiva do orifício que se for circular é de $\frac{\pi D^2}{4}$.

Caso tenhamos mais de um orifício, basta acrescentar um fator $n_{orif}$ multiplicando a vazâo gerada por 1 orifício.

2.2 – Detalhes da Equação do Orifício

Algumas nuâncias devem ser consideradas.

1. Um orifício nem sempre está na base do reservatório. Vamos assumir que ele tem uma certa altura $h_o$, tomada do fundo do reservatório
2. A altura efetiva do orifício não é tomada em relação à sua base, mas sim em relação ao seu centro de gravidade ou centro hidráulico

Desse modo, vamos assumir que a carga hidráulica efetiva em orifícios ($\hat{h}$) seja naturalmente função de $h_o$ e do seu centro geométrico

A forma como vamos determinar o centro hidráulico para o cálculo da carga efetiva do orifício pode ser dada como $h_{min} = 0,2.D_h$, onde $D_h$ é o diâmetro hidráulico da seção.

Caso queira saber mais sobre diâmetro hidráulico, veja esse artigo aqui.

Em linhas gerais, o diâmetro hidráulico de uma seção circular é justamente igual ao seu diâmetro $D$.

Assim, podemos escrever a carga efetiva do orifício como:

$$
\hat{h}(t) = \max{\left(h(t) – \max{(h_o + D_h/2,h_o + h_{min})}\right)} \tag{5}
$$

Onde $\max{(x,y)}$ é a função que calcula o máximo entre $x$ e $y$ $\in \mathbb{R}$.

Desse modo, a equação anterior diz que a pressão efetiva no orifício é a altura subtraída de uma altura tal que represente o maior valor entre 20% do diâmetro hidráulico e a altura do orifício.

2.2.1 – Lei dos Orifícios Grandes e Pequenos 

Na verdade, o regime de escoamento em orifícios tem pelo menos 3 tipologias. Primeiro, vamos imaginar que o orifício está no fundo do reservatório e que o reservatório esteja inicialmente vazio.

Nesse caso, como se dá o escoamento caso a lâmina d’água seja menor que $D_h/2$? Essa seria a primeira parte da cota-descarga dos orifícios.

Teoricamente a água não escoaria nesse caso.

Assim, modelamos esse escoamento “empiricamente” como:

$$
Q_{out}^o = f.C_d^o.A_{ef}.\sqrt{(h – h_o)} \tag{6}
$$

Onde $f$ é um fator que pode variar entre 0.1 e 0.5, geralmente.

2.2.2 – Lei dos Grandes Orifícios

Logo adiante, vamos aumentando a altura no reservatório de modo que agora ela segue $D_h/2 \leq h \leq 3D_h$ Essa relação anterior diz respeito a um Grande Orifício, isto é, onde as dimensões do orifício são quase que de mesma ordem de magnitude da altura d’água.

Portanto, nesse caso, a vazão do orifício, caso ele seja retangular, é dada por:

$$
Q_{out}^o = \frac{2}{3}.C_d.A_{ef}.\sqrt{2g}.\frac{\left(h_2^{3/2} – h_1^{3/2}\right)}{(h_2 – h_1)} \tag{7}
$$

Onde $h_2$ é a altura d’água acima do base do orifício e $h_1$ a altura d’água tomada em relação ao topo do orifício.

No caso de orifícios grandes circulares as derivações matemáticas ficam complexas e geralmente essa hipótese é desprezada.

Finalmente, caso tenhamos um orifício afogado de modo que $(h – h_0 – D_h/2) > 3D_h$, usamos a equação básica de orifícios ja mostrada anteriormente.

2.3 – Modelo Hidráulico de Vertedouros para Amortecimento de Cheias em Reservatórios 

Há diversos tipos de veretedouros disponíveis (e.g., francis, creager). 

Um dos mais comunmente aplicados é o vertedor tipo Francis. Vertedores podem ser classificados entre vertedores de soleira delgada e soleira espessa.

O Francis é um que pode ser classificado como vertedor de soleira espessa. Ele basicamente é um corte na região do topo do reservatório que direciona o fluxo.

Esse fluxo ao passar pelo vertedor pode ter contrações laterais ou não.

2.3.1 – Contrações Laterais e Perdas de Carga

Essas contrações aumentam ou diminuem o grau de perda de carga quando o fluxo sai do reservatório. Além disso, há uma região logo abaixo ao tirante de lâmina (veia líquida) que saí do vertedor onde há a entrada de ar.

Fenômenos fluidodinâmicos complexos podem acontecer na saída do vertedor e são geralmente explicados pelo seu coeficiente de descarga $C_d^s$.

Vertedores tipo Francis têm equação cota-descarga dada pela seguinte forma:

$$
Q_{out}^s = C_d^s . L_{ef} . (\max{(h(t) – p,0)})^{3/2} \tag{8}
$$

Onde $Q_{out}^s$ é a vazão que saí pelo vertedor, $L_{ef}$ é o comprimento efetivo da soleira do vertedor e $p$ é a altura do vertedor, tomada do fundo do reservatório.

2.4 – Curva Cota-Descarga de Reservatórios

Finalmente, de posse das curvas cota-descarga de orifícios e vertedores, podemos escrever uma “lei” que prediz para cada altura $h(t)$ qual a vazão, de modo que:

$$
Q_{out}(h(t)) = Q_{out}^o(h(t)) + Q_{out}^s(h(t)) = C_d.A_{ef}.\sqrt{2g(\hat{h}(t))} + C_d^s . L_{ef} . (\max{(h(t) – p,0)})^{3/2} \tag{9}
$$

2.5 – Formas de Resolução da Equação de Balanço de Massa

A equação \eqref{equ:mass_balance} pode ser resolvida de diversas formas. Primeiro vamos resolve-la do jeito mais simples, usando um esquema numérico explícito.

2.5.1 – Método Explícito para Amortecimento de Cheias em Reservatórios 

Um método numérico explícito é tal que toda e qualquer informação modelada no intervalo de tempo ($t + \Delta t$) depende exclusivamente de informações já obtidas no intervalo de tempo ($t$).

Assim, podemos aproximar as equações diferenciais para quantidades finitas, da seguinte forma:

$$
\frac{\mathrm{d}S(t)}{\mathrm{d}t} \approx \frac{S(t + \Delta t) – S(t)}{\Delta t} = Q_{in}(t) – Q_{out}(t) \tag{10}
$$

Não sei se você notou, mas a equação anterior pode ter problemas de instabilidade caso o time-step adotado seja muito grande.

Em métodos totalmente explícitos, devemos garantir estabilidade dos métodos numéricos com as condições de Courant.

Não vou entrar em méritos muito avançados nesse artigo, mas vamos assumir que temos um passo de tempo pequeno demais que não cause instabilidade.

Assim, podemos isolar termos do time-step da frente ao lado esquerdo da equação e os termos que dependem do time-step atual do lado direito da equação, resultando em:

$$
S(t + \Delta t) = S(t) + \Delta t(Q_{in}(t) – Q_{out}(t)) \tag{11}
$$

Essa equação charmosa anterior é facilmente resolvida adotando um time-step pequeno, sabendo os hidrogramas de entrada e modelando o hidrograma de saída pelas equações da hidráulica mostradas anteriormente.

2.5.1.1 – Vantagens e Desvantagens do Método Explícito

O método é simples e relativamente fácil de ser programado.

Não requer tabelas auxiliares.

Porém, o método requer pequenos time-steps que muito provavelmente vao ter resolução maior (i.e., intervalos de tempo menores) que os dados de entrada do hidrograma de entrada.

Isso implica que você talvez tenha que interpolar os dados da vazão de entrada para valores entre intervalos de tempo conhecidos.

Seu hidrograma de entrada seria uma escadinha, com valores constantes entre dois valores conhecidos no hidrograma de entrada.

2.5.2 – Método PULS – Amortecimento de Cheias em Reservatórios

Aparentemente Puls publicou esse método em meados dos anos 30, no século passado.

Frequentemente na literatura internacional, esse método é chamado de Level Pool Routing (LPR).

Ele é, diferentemente do método explícito, é um método semi-implícito.

Isso significa que há uma conexão entre variáveis de estado do tempo da frente com variáveis de estado do tempo atual, de modo que não há uma relação unívoca entre eles.

2.5.2.1 – Formulação Matemática

Vamos retornar a equação básica de balanço de massa dada na Eq. \eqref{equ:mass_balance}.

Uma hipótese razoável é assumir que a equação diferencial pode ser escrita em forma de diferenças finitas, isto é:

$$
\frac{\mathrm{d}S(t)}{\mathrm{d}t} \approx \frac{S(t+\Delta t) – S(t)}{\Delta t} = \frac{Q_{in}(t + \Delta t) – Q_{in}(t)}{2} – \frac{Q_{out}(t + \Delta t) – Q_{out}(t)}{2} \tag{12}
$$

Perceba que sabemos vários termos da equação anterior.

Basicamente, tudo que depende do tempo $t$ é conhecido.

Além disso, $Q_{in}(t+\Delta t)$ também é conhecido e vem justamente do estudo hidrológico que determina o hidrograma de entrada.

Assim, podemos separar termos conhecidos e desconhecidos, um em cada lado da equação. Vejamos:

$$
\frac{2S(t + \Delta t)}{\Delta t} – Q_{out}(t + \Delta t) = \frac{2S(t)}{\Delta t} – Q_{out}(t) + Q_{in}(t + \Delta t) + Q_{in}(t) \tag{13}
$$

As variáveis de estado do tempo $t + 1$ dependem das variáveis do estado $t$, nesse caso, e sabendo-se as condições iniciais (e.g., dados quando $t = 0$) podemos resolver a equação.

Assim, basta resolver essa equação dinâmica por toda a duração do seu tempo indo desde o tempo inicial até o fim da simulação.

2.5.2.2 – Tabelas Auxiliares – Amortecimento de Cheias em Reservatórios (PULS)

Antigamente não se tinha muito poder computacional.

Resolver problemas de otimização eram complicados.

Assim, muitos dos problemas eram resolvidos com gráficos, alguns até adimensionais para facilitar.

Esse é um dos casos do método PULS Em geral, cria-se colunas contendo o seguinte:

Tabela auxiliar
2.S/t + Q (m3/s)	S(h) (m)	Cota (m)	h (m)	2S/t (m3/s)	Qorif (m3/s)	Qvert (m3/s)	Qorif + Qver (m3/s)

1. Primeiro entra-se com uma coluna que tenha as alturas saindo de 0 até o valor da altura máxima do reservatório
2. Com as alturas e com a curva cota-volume, estima-se $S$ para cada $h$, divide-se por $\Delta t$. Perceba que você pode ter a função $S(t)$ tabelada tanto como uma equação contínua (e.g., $S(h) = k.h^n$, onde $k$ e $n$ são calibrados.
3. Calcula-se depois as vazões no orifício e no vertedor usando as equações de orificío e vertedor

Essa tabela auxiliar serve para você entrar com o valor de $2S/\Delta t + Q$ e obter os valores de $Q_{out}^o$ e $Q_{out}^s$.

Você não está fazendo nada mais do que resolvendo um problema que tem uma equação diferencial, quebrada em diferenças finitas, resolvida com um método semi-implícito.

Vamos Resolver um Exemplo

3 – Dimensionamento de Reservatório

3.1 – Exercício 01

Primeiro vamos fazer um exercício bem simples e básico. Suponha que você queira verificar como se da a propagação de vazão em um reservatório pelo método PULS, os seguintes dados: Dados da bacia

1. A = 3 km2
2. $t_c$ = 60 min
3. CN = 85
4. IDF – (K = 826.806, a = 0.143, b = 13.326, c = 0.793)
5. Tempo de Retorno = 25 anos
6. Chuva em Blocos Alternados
7. Volume morto correspondente a 10 cm, ou seja, o orifício inicia-se a 10 cm do fundo
8. Área do Rervatório
9. Abatimento mínimo para TR de 25 anos = 50% do pico
10. Reservatório inicialmente vazio ou seja, h(0) = 0 m

O problema é altamente iterativo. Mas antes, deixa eu te mostra como você pode construir uma tabela que tenha todos os cálculos

3.1.1 – Exemplo de Tabela

1. Crie uma coluna para o passo indo de $1$ até $n$, onde $n$ é o último passo
2. Depois entre com o tempo, de modo que o tempo é o passo multiplicado pelo intervalo de tempo dos cálculos
3. A cota vai ser calculada, mas no caso inicial, vamos imaginar que o reservatório esteja vazio e portanto ela seja a cota de base do reservatório
4. $I_1$ é a entrada que vem do hidrograma de entrada para o tempo atual
5. $I_2$ é a vazão do tempo da frente
6. $h$ é a altura do reservatório
7. $Q_{orif}$ é a vazão do orifício, que vai vir na verdade da tabela auxiliar usando funções de procura como por exemplo o Procv
8. $Q_{vert}$ segue o mesmo raciocínio
9. Q1 é a soma da vazão do vertedor com a vazão do orifício
10. $S_1$ é o volume, que também pode vir da tabela auxiliar, mas no primeiro tempo é conhecido
11. Finalmente vem o fator que é usado na tabela auxiliar. Calcule ele e vá para a tabela auxiliar coletar $Q_{orif2}$, $Q_{vert2}$, $S_2$ e $Q_{out}$
12. Associe os valores calculados anteriormente com os valores iniciais na linha de baixo para $Q_{orif1}$, $Q_{vert1}$, $S_1$ e $Q_{out1}$
13. Repita o processo até propagar todo o hidrograma

3.1.2 – Resultados da Simulação – Amortecimento de Cheias em Reservatórios

A tabela abaixo mostra o resultado numérico da simulação

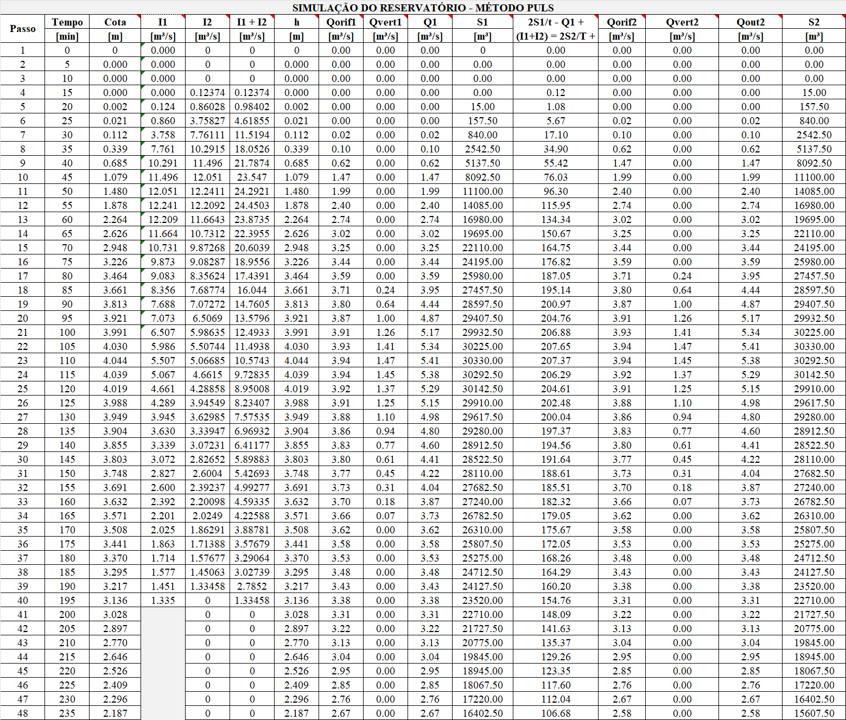
As figuras adiante mostram a curva cota-área, cota-descarga e cota-volume, além do hidrograma efluente ao reservatório. 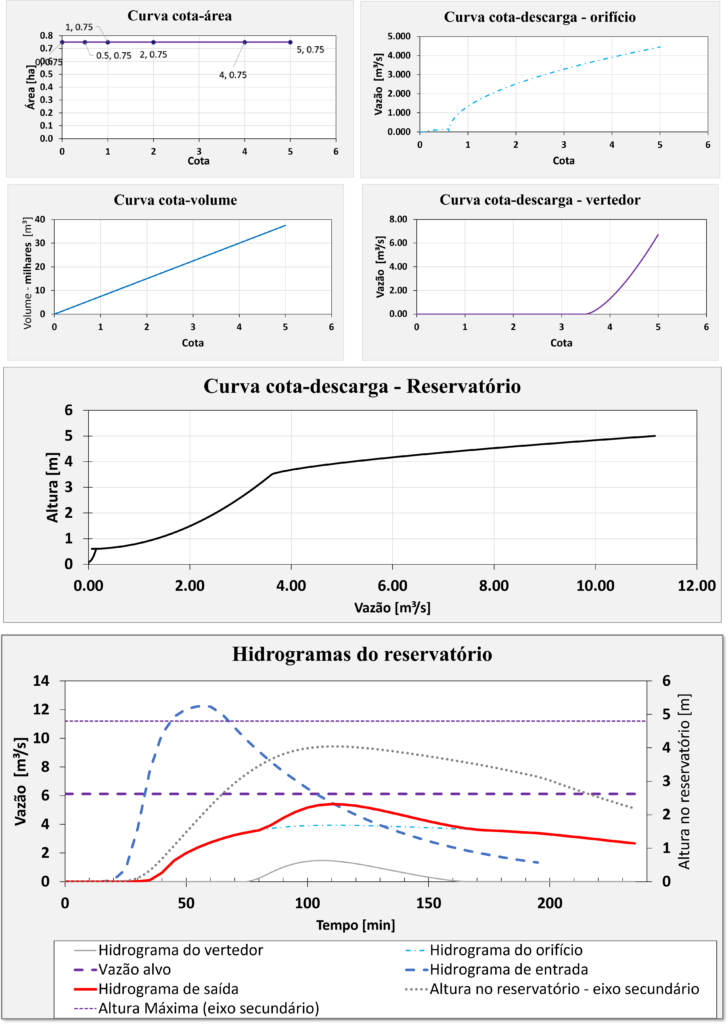Perceba que a linha roxa mede nossa vazão alvo e que estamos abaixo do limite que consideramos 50% da vazão de pico)

Perceba também que, caso tenhamos uma cota máxima maximorum de projeto no valor 4.80 metros, também estamos abaixo do limite.

Além disso, veja que tivemos um pouco de escoamento pelo vertedor na linha cinza.

3.1.3 – Resultados para TR = 100 anos

E se agora uma chuva de 100 anos ocorrece? Qual seria a eficiência do reservatório?

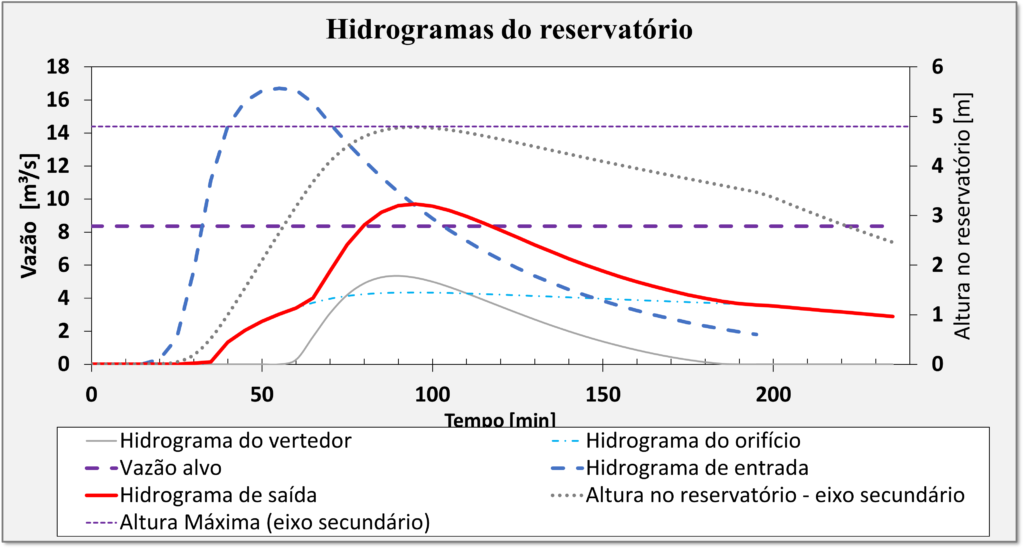
Veja no grafico anterior alguns detalhes:

1. Nosso reservatório falhou em reduzir a vazão de pico em 50% pois a linha vermelha esteve acima da linha roxa em alguns momentos para TR = 100 anos
2. Porém, não atingimos a cota máxima maximorum do reservatório, apesar de quase tangenciarmos ela (perceba a linha roxa pontilhada fina com a linha cinza pontilhada)
3. O vertedor foi bem utilizado chegando a soltar uma vazão de pico de aproximadamente $5~m^3/s$, o que está ok
4. Nessas condições, nosso reservatório tem uma ótima eficiência de projeto para TR = 25 anos e uma eficiência relativamente boa para TR = 100 anos

3.2 – Exempo mais Realista de Projeto – Amortecimento de Cheias em Reservatórios (Otimização)

Vamos imaginar que você vai ganhar R$ 30.000,00 para fazer um projeto de um reservatório, que tenha a menor área possível para uma altura máxima de 4.80 m.

Você vai concorrer com diversos engenheiros que não entendem de otimização, mas você entende. Porém você tem algumas restrições mais ou menos complicadas, vejamos abaixo.

1. Primeiro, ele vai ter que suportar uma chuva de 100 anos mas você vai ter algumas restrições geométricas
2. O máximo comprimento do vertedor é 2 m
3. O orifício deve ser retangular, com base no máximo de 1 m e altura de no máximo 1.20 m
4. O número máximos de orifícios no reservatório é 4
5. A cota do vertedouro pode variar entre 3.00 m e 3.80 m em relação ao fundo do reservatório
6. A altura máxima maximorum do reservatório é 4.80 m
7. Os orifícios serão colocados no fundo do reservatório, ou seja, $h_o$ = $0 m$.
8. A vazão de pico deve ser amortecida em 50% para TR = 100 anos
9. A área máxima disponível para implantação do reservatório é de 3 ha.

A pergunta é: Qual a área mínima do reservatório que atende essas restrições?

3.2.1 – O que você pode alterar?

• Área do Reservatório
• Largura do vertedor
• Sua cota
• Número de orifícios
• Sua altura
• Sua base

Vamos assumir os mesmos dados da bacia do exemplo anterior

1. A = 3 km2
2. tc = 60 min
3. CN = 85
4. IDF – (K = 826.806, a = 0.143, b = 13.326, c = 0.793)
5. Chuva em Blocos Alternados

3.2 – Resolução do problema – Amortecimento de Cheias em Reservatórios

Não tem jeito … Ou criamos um problema de otimização e colocamos as restrições escritas por mim na descrição do problema e resolvemos isso da maneira mais elegante possível ou então vamos para o velho tentativa e erro com uma planilha eletrônica.

Como são muitas restrições, vou formular um problema de otimização para resolver isso. Para isso, devemos definir uma função objetivo.

Nesse caso, queremos minimizar a área do reservatório, portanto nossa função objetivo é justamente minimizar a área dele.

Nossas variáveis de decisão já foram descritas anteriormente, mas podemos formular o problema assim:

1. Minimizar uma função de erro que penalize soluções que extrapolam a vazão de pico
2. Esta função deve estar restrita as condições do problema, que são:
   1. Variáveis de Decisão: Geometria do problema e propriedades dos vertedores e orifícios (e.g., coeficientes de descarga);
   2. Valores mínimos e máximos estabelecidos para cada variável de decisão

Caso queira saber mais sobre a formulação mais precisa de problemas de otimização, veja esse artigo de minha autoria, abaixo:

Disponível gratuitamente em: https://ascelibrary.org/doi/full/10.1061/%28ASCE%29WR.1943-5452.0001588

Para resolvermos esse problema podemos utilizar a ferramenta Solver do Excel.

Nosso problema é não linear e não convexo, portanto vamos resolve-lo utilizando técnicas de algoritmos evolucionários.

Essas teorias mais complexas de otimização não vão ser tratadas aqui nesse artigo, caso tenha mais interesse em otimização, veja esse artigo de minha autoria ou esse vídeo.

Uma solução rápida para esse problema mas com maiores chances de ser um ótimo local é usar o método GRP não linear. Veja a solução otimizada encontrada abaixo:

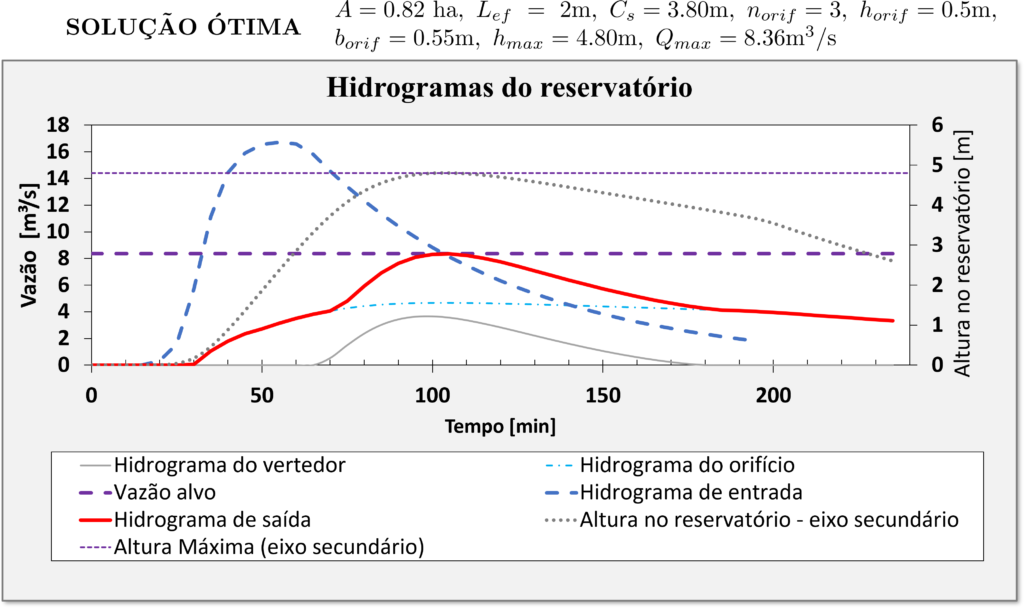
Note algumas coisas:

1. Estamos no limite da vazão tolerável de projeto
2. Também estamos no limite da altura máxima tolerável no reservatório
3. Perceba que só conseguimos atingir os dois itens anteriores pois otimizamos a área do reservatório
4. Caso a área fosse menor, aumentaria-se o nível d’água e não seria possível garantir nossa restrição de nível máximo
5. Além disso, caso diminuíssimos a área aumentaria o nível e por consequência a vazão, fazendo com que nossa restrição de vazão não fosse satisfeita
6. Esse é o valor ótimo, muito provavelmente um ótimo global, mas não temos garantias pelo método
7. Entretanto, o valor é muito bom e nos diz um dimensionamento que dificilmente conseguiriamos fazer na base da tentativa e erro
8. Veja também que o algorítmo de otimização nos deu resultados interessantes para os orifícios. Eles, em linhas gerais, são baixos, mas usamos 4 orifícios. Dessa forma, garantimos uma maior eficiência pois eles trabalharão a maior parte como pequenos orifícios afogados e em grande quantidade

4 – Conclusões

Veja bem, você não precisa ser um gênio da matemática para entender que é muito tedioso resolver problemas dinâmicos em que cálculos têm de ser feitos em tabelas.

As planilhas estão ai pra isso, pra te possibilitar pensar e ter tempo de fazer análises mais criteriosas.

Foi-se o tempo que nós, engenheiros, arquitetos, profissionais em áreas correlatas à engenharia, deveriamos saber apenas como “dimensionar”.

Aliás, a grade dos nossos cursos quase se quer fala em otimizar. Otimizar projetos é muito mais interessante do que apenas dimensionar.

Nesse artigo te mostrei como ter uma base mais sólida é fundamental para entender o que fazer em projetos mais complexos.

Para te ajudar, caso queria ter acesso a minha planilha, deixo o link disponível aqui abaixo: https://engenheiroplanilheiro.com.br/produto/calculo-de-bacias-de-detencao-metodo-puls/

Fico à disposição! Desejo sucesso a você meu caro(a) Um grande abraço e seja bem-vindo ao meu site Marcus.