Pré dimensionamento de Piscinões
Um dos principais objetivos do pré-dimensionamento de piscinões, ou técnicamente bacias de detenção, é determinar seu volume mínimo e sua área média para atender determinada condição de projeto.
Assim, bacias de detenção são estruturas de reservação com o objetivo de armazenar parte do volume de escoamento superifical e, portanto, retardar picos de vazão.
Entretanto, seus métodos de dimensionamento podem variar significativamente com base na etapa de projeto.
Em análises mais sofisticadas, o recomendado é a análise via método PULS. Caso queira ver mais sobre isso, leia esse artigo.
Por outro lado, outros métodos mais rápidos e simples também são de grande valia para análises preliminares e estudos de viabilidade.
Um desses casos é apresentado nesse artigo.
2.0 – Método do Impacto Zero
Vamos imaginar que temos uma condição de impermeabilização e, portanto, de aspectos hidrológicos antes do processo de urbanização.
A esse cenário damos o nome de pré-urbanização.
Devemos dimensionar um reservatório que consiga, de certa forma, fazer com que as condições de escoamento sejam parecidas com as condições de pré-urbanização.
Assim, nosso objetivo é restringir a vazão de saída do reservatório a uma vazão menor ou igual a vazão de pico de pré-urbanização.
3.0 – Metodologia de Cálculo
Como estamos falando de um método simplificado, hipóteses simplificadoras são assumidas:
- Hidrogramas tanto de pré quanto de pós urbanização são estimados pelo método racional
- Tempos de concentração são adotados, podendo ser inclusive iguais tanto para pré-urbanização quanto para pós-urbanização
- O orifício de fundo ou bomba hidráulica deve ser dimensionada para ter a capacidade da vazão de pré-urbanização
3.1 – Hidrogramas de Pré e Pós Urbanização – Pré Dimensionamento de Piscinões
3.1.1 Vazão de pico de pré-urbanização – Método Racional
$$
Q_{pre}^p = C_{pre}.i_{pre}.A \tag{1}
$$
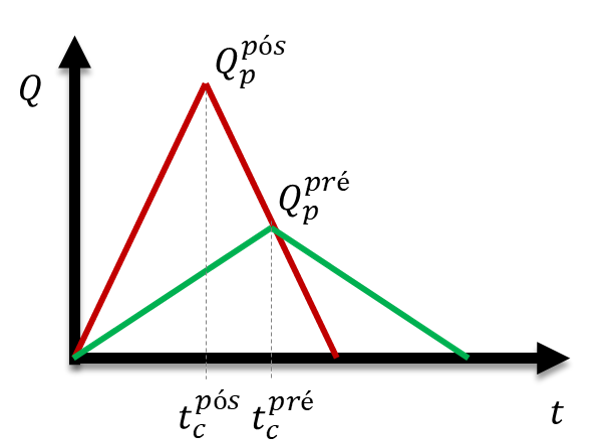
3.1.2 Declividades do Hidrograma e Regras de Escoamento
O hidrograma tem uma fase ascendente e uma descendente.
Ambas fases são descritas pela declividade $\alpha$.
$$
\alpha_{pre} = \frac{Q_{pre}^p}{t_c^{pre}} \tag{2}
$$
$$
Q_{pre}(t) = \alpha_{pre}.t \text{Se }t \leq t_c \label{equ:pre1} \tag{3}
$$
$$
Q_{pre}(t) = Q_p^{pre} – \alpha_{pre}.(t – t_c^{pre}) \text{Se } t_c^{pre} \leq t \leq 2.t_c^{pre} \label{equ:pre2} \tag{4}
$$
$$
Q_{pre}(t) = 0 \text{Se } t \geq 2.t_c^{pre} \label{equ:pre3} \tag{5}
$$
onde $Q_{pre}$ é a vazão de pós urbanização, $i_{pre}$ é a intensidade de precipitação de pré-urbanização, $C_{pre}$ o coeficiente de runoff de pré-urbanização, $A$ é a área de drenagem e $t$ é o tempo.
3.1.3 Vazão de pico de pós-urbanização – Método Racional
De maneira similar ao apresentado na seção anterior, as vazões podem ser estimadas
$$
Q_{pos}^p = C_{pos}.i_{pos}.A \tag{6}
$$
3.1.4 Declividades do Hidrograma e Regras de Escoamento
$$
\alpha_{pos} = \frac{Q_{pos}^p}{t_c^{pos}} \tag{7}
$$
$$
\label{equ:pos1} Q_{pos}(t) = \alpha_{pos}.t \text{Se }t \leq t_c^{pos} \tag{8}
$$
$$
Q_{pos}(t) = Q_p^{pos} – \alpha_{pos}.(t – t_c^{pos}) \text{Se } t_c^{pos} \leq t \leq 2.t_c^{pos} \label{equ:pos2} \tag{9}
$$
$$
Q_{pos}(t) = 0 \text{ Se } t \geq 2.t_c^{pos} \label{equ:pos3} \tag{10}
$$
Onde $Q_{pos}$ é a vazão de pós urbanização, $i_{pos}$ é a intensidade de precipitação de pós-urbanização e $C_{pos}$ o coeficiente de runoff de pós-urbanização.
3.2 – Volume mínimo do reservatório
O volume mínimo do reservatório é dado pela máxima diferença entre os volumes de entrada e saída do reservatório.
Matematicamente falando, podemos escrever que o volume mínimo é:
$$ \label{equ:vol_min}
V_{min} = \mathrm{argmax}_{t \in \tau}{\int_{0}^{t}\left( Q_{pos}(t) – Q_{pre}(t) \right)\text{dt}} \tag{11}
$$
onde $\tau$ representa o sub-espaço representado pelo tempo de análise dos cálculos.
Nós podemos resolver a integral anterior via somatório, utilizando diferenças finitas.
Em outras palavras, basta criar uma coluna calculando o volume acumulado de entrada e outra calculando o volume acumulado de saída.
A diferença máxima entre eles é justamente o volume mínimo do reservatório.
3.3 – Área do Reservatório
Vamos imaginar que o material de enchimento do reservatório tenha uma porosidade $\eta$.
Assim, para determinarmos a área mínima do reservatório podemos utilizar a equação de volume de um prisma, de modo que:
$$
A_r = \frac{V/\eta}{h} \tag{12} \label{equ:area}
$$
onde $h$ é a altura de projeto do reservatório, $A_r$ é a área do reservatório, $V$ é o volume do reservatório e $\eta$ é sua porosidade ($0 \leq \eta \leq 1$).
Por exemplo, caso você esteja dimensionando uma caixa de areia ou um jardim de biorretenção, você pode fazer a média ponderada das porosidades de cada material que compõem o reservatório.
Segue aqui uma recomendação de valores para porosidade.
3.3 – Diâmetro máximo do orifício
Muito bem, o diâmetro do orifício pode ser calculado aplicando-se a conservação da energia saindo do topo do reservatório a linha central do orifício.
No entanto, o orifício pode ter várias seções e, dependendo de sua geometria, pode ser considerado um grande ou pequeno orifício.
Se quiser saber mais sobre isso, leia esse artigo onde detalho mais sobre as condições de escoamento de orifícios.
Assim, podemos assumir que o orifício é um grande orifício e que sua vazão é dada por:
$$
Q = n.C_d. A_{ef} . \sqrt{(2g(h – h_o – h_c))} \tag{13} \label{equ:orificio}
$$
onde $n$ é o número de orifícios, $C_d$ é o coeficiente de descarga do orifício, $A_{ef}$ sua área transversal ao escoamento, $g$ é a aceleração da gravidade, $h_o$ é a altura medida da geratriz inferior do orifício em relação à base do reservatório e $h_c$ é a altura do centro da seção (e.g., no caso de orifícios circulares essa altura é $D/2$).
Isolando $D$ na equação (\ref{equ:orificio}), desprezando a altura $h_c$ e $A_{ef} = \pi.D^2/4$, vem que:
$$
D = \frac{\left(\frac{Q}{n}\right)}{\frac{\pi.C_d}{4}2g(h – h_o)} \tag{13}
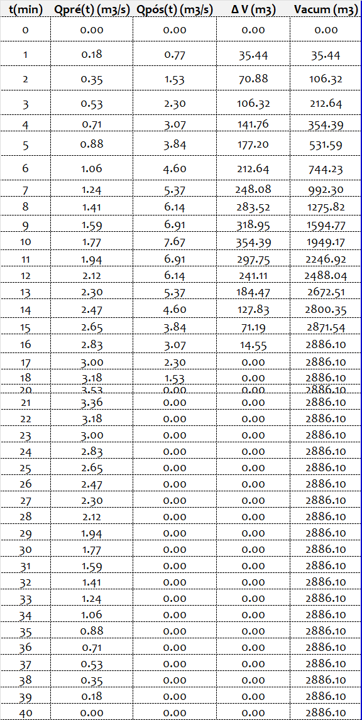
$$
3.4 – Esquema da Planilha
Seguindo a descrição da planilha, podemos resolver o sistema de equações dinâmicas apresentadas acima em uma tabela de excel.
Colocamos o tempo em minutos, a vazão de pré-urbanização, de pós urbanização, a variação dos volumes entre cada caso e o volume acumulado, um em cada coluna.
Ai basta resolver as equações (\eqref{equ:pre1}), (\eqref{equ:pre2}), (\eqref{equ:pre3}), (\eqref{equ:pos1}), (\eqref{equ:pos2}) e (\eqref{equ:pos3}) dinamicamente ao longo do tempo.
Após a duração máxima de cálculo $t_f$, basta aplicar a equação (\eqref{equ:vol_min}), adotar os dados do reservatório e resolver a equação \eqref{equ:area} e \eqref{equ:orificio}.
4.0 – Exemplo de Pré dimensionamento de Piscinões
De antemão, vamos pré-dimensionar um piscinão para atender uma vazão de pré e urbanização equivalente a um tempo de retorno de 10 anos.
Além disso, vamos simplificar e assumir que a mesma curva IDF é válida para as condições de pré e pós urbanização, apesar de teoricamente o padrão de chuvas poder mudar.
Entretanto, vamos assumir diferentes tempos de concentração e consequentemente diferentes intensidades de precipitação.
- $A$= 0.24 km2
- $C_{pre}$ = 0.35
- $i_{pre}$ = 152.42 mm/hr
- $t_c^{pre}$ = 20 min
- $C_{pos}$ = 0.677
- $i_{pos}$ = 170 mm/hr
- $t_c^{pos}$ = 10 min
- $C_d$ = 0.61
- $h_o$ = 0.2 m
- $h$ = 3 m
- $n$ = 1
- Intervalo dos cálculos = 1 min
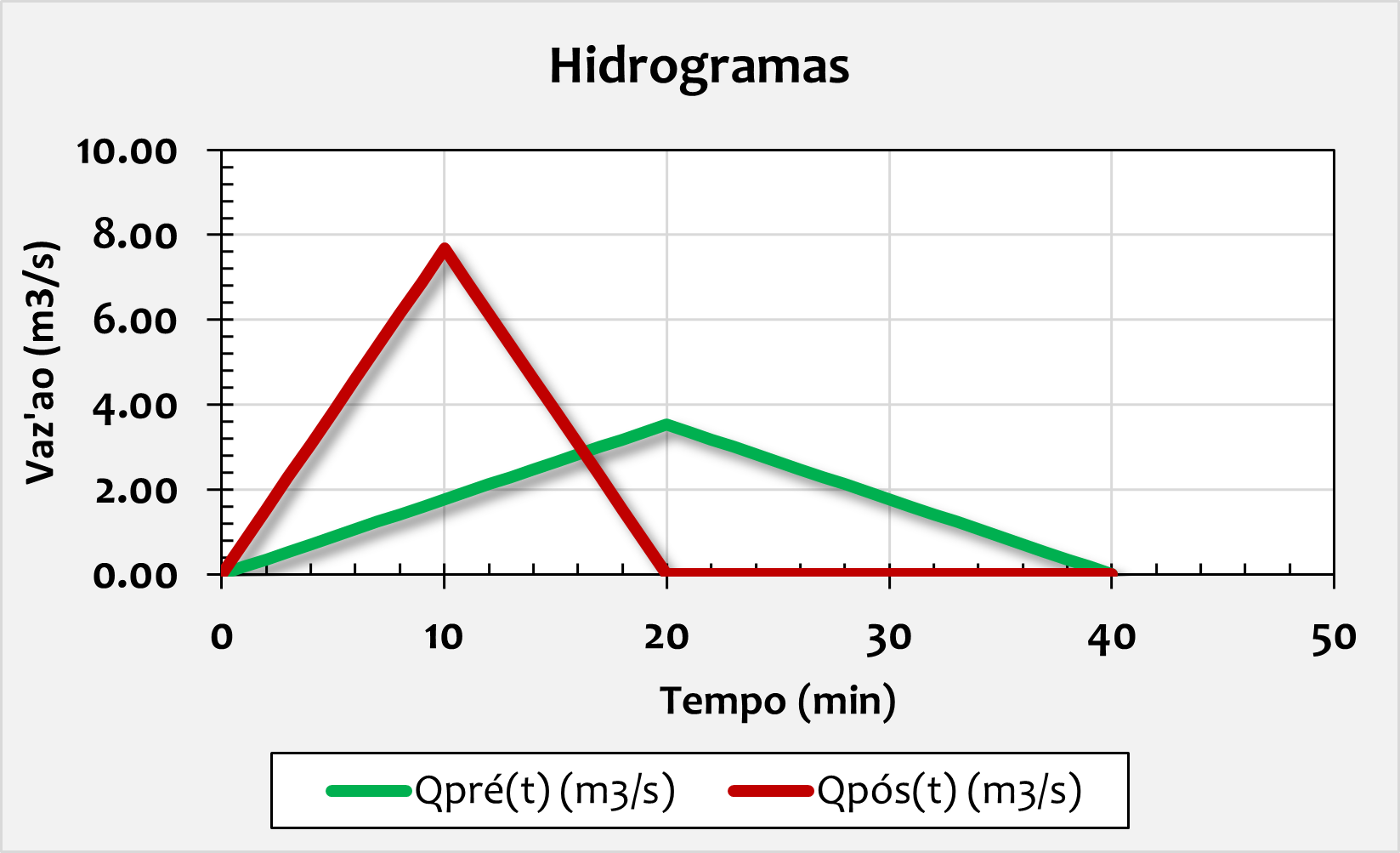
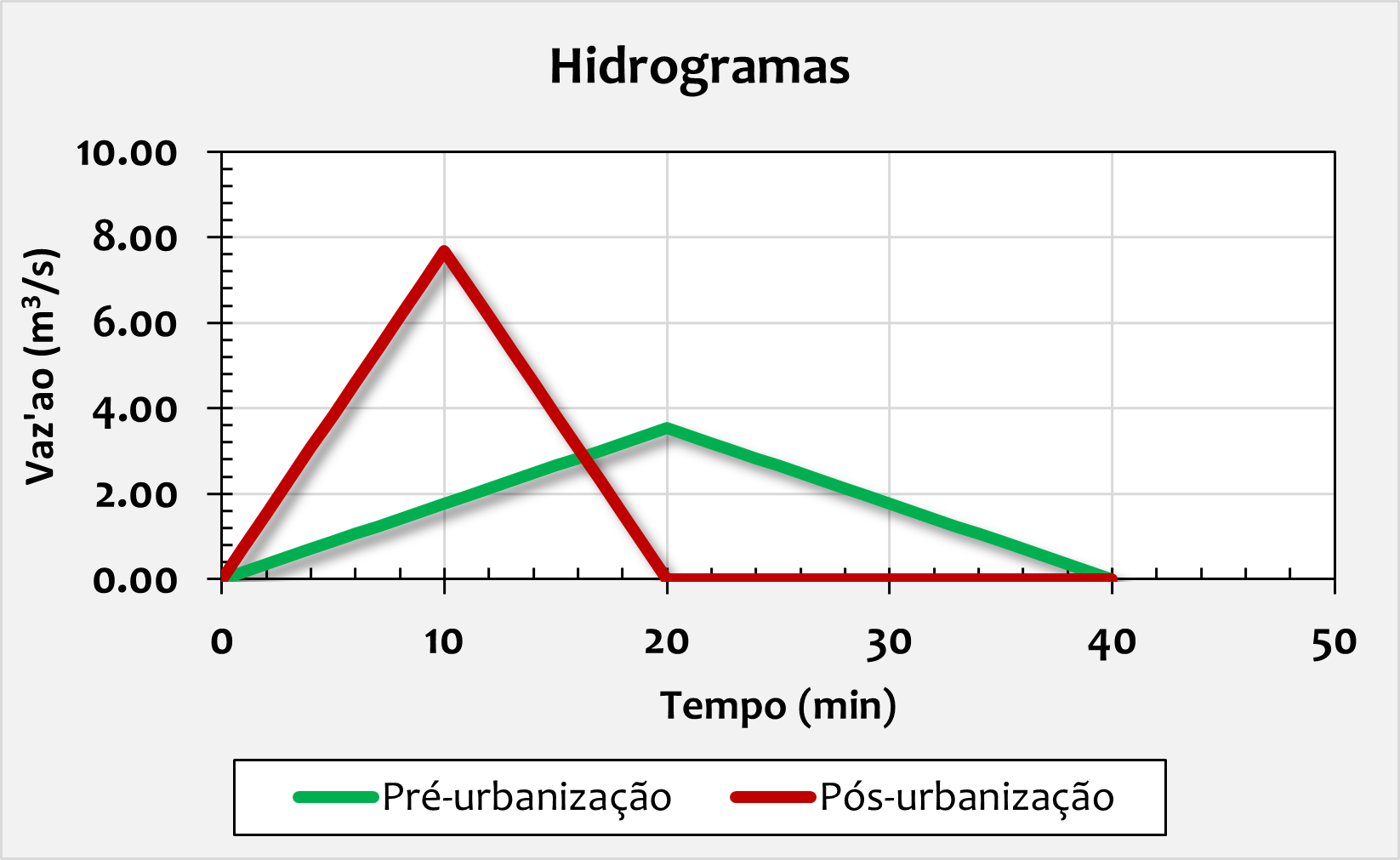
4.1 – Hidrogramas
Desse modo, as figuras a seguir representam os hidrogramas de pré e pós urbanização, além de representar a solução numérica.
5.0 – Conclusões
- Finalmente, reservatórios de detenção podem ser rapidamente dimensionados com métodos relativamente simples e os resultados podem indicar uma boa relação com a realidade.
- O orifício dos reservatórios devem ser dimensionados para a vazão de pré-urbanização
- Para dimesionamentos mais criteriosos, recomendamos a aplicação de métodos hidraulicos de amortecimento de cheias.
- Nesse artigo apresentamos o método do impacto zero que leva tem por objetivo dimensionar um reservatório que atenda as condições de volume e vazão de pré-urbanização.
Caso tenha interesse na planilha, entre em contato comigo pelo whatsapp ou pelo meu email ([email protected])
