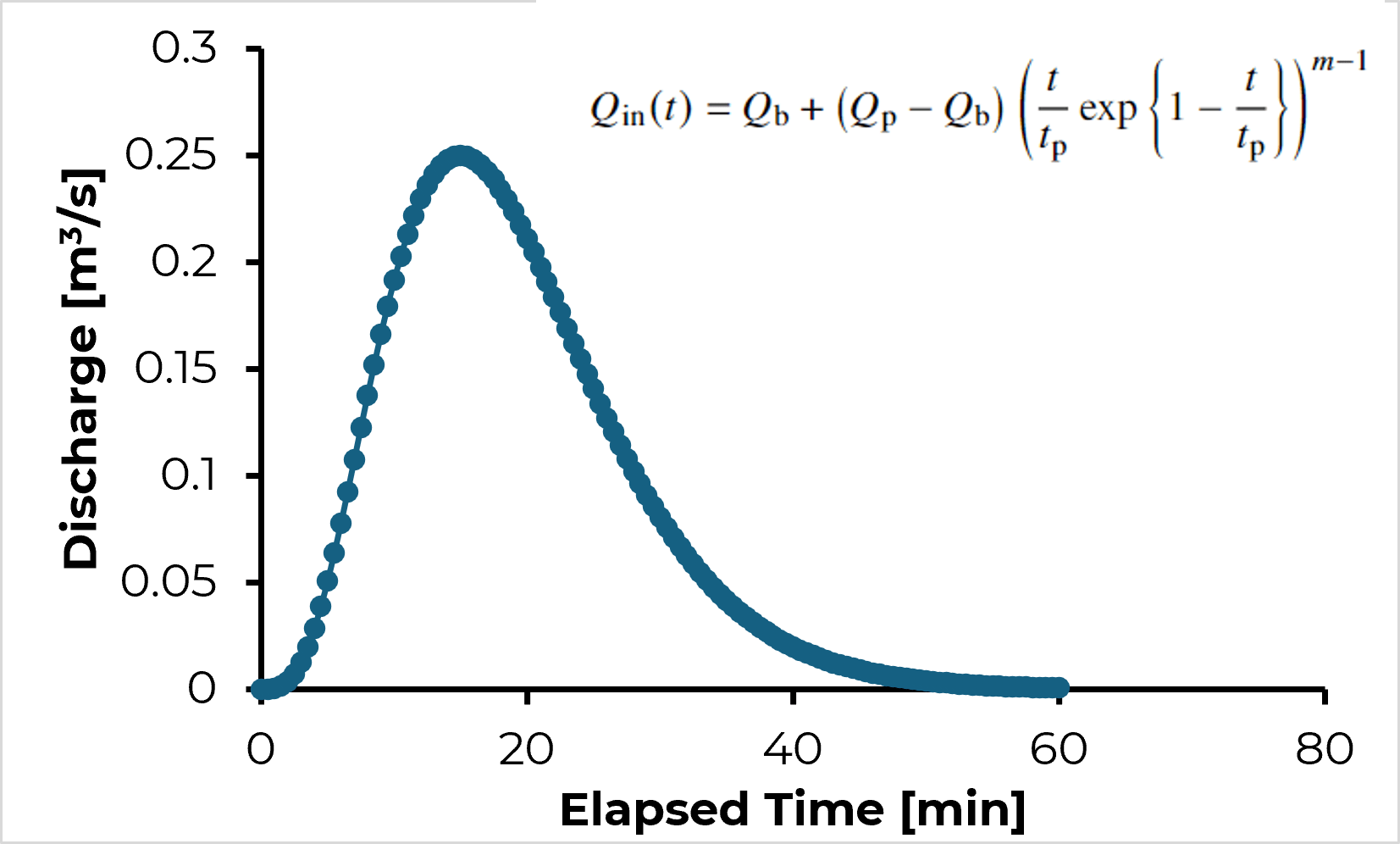
Hidrograma de Nash
Diversas formulações para a determinação de hidrogramas unitários são disponíveis.
Uma delas é o uso de uma função Gamma de dois parâmetros para explicar como a resposta de uma bacia se comporta perante um pulso de precipitação.
De maneira geral, um hidrograma pode ser expresso por:
$$Q_{\mathrm{in}}(t)=Q_{\mathrm{b}}+\left(Q_{\mathrm{p}}-Q_\mathrm{b}\right)\left(\frac{t}{t_\mathrm{p}} \exp \left\{1-\frac{t}{t_\mathrm{p}}\right\}\right)^{m-1}$$
onde $Q_{\mathrm{in}}$ é o hidrograma de entrada, $Q_b$ = vazão de base, $Q_p$ = vazão de pico e $Q_p – Q_b$ = vazão de pico do escoamento superficial. O parâmetro $m$ é um fator de forma do hidrograma.
A vazão de pico $Q_s = (Q_p – Q_b)$ é relacionada com o tempo de pico $t_p$, volume de escoamento superficial $V_r$ e com outro parâmetro de forma $b$, de modo que:
$$Q_{\mathrm{s}} = \frac{bV_r}{t_p}$$
Além disso, os parâmetros $b$ e $m$ são relacionados da seguinte forma:
$$ b=\frac{(m-1)^m}{\Gamma(m) e^{m-1}} $$
onde $\Gamma$ é a função gamma dada por $( m – 1)$! (fatorial).
Por exemplo, se $b = 0.75$, esse é exatamente o caso do fator de pico do método SCS. Resolvendo a equação anterior para $b = 0.75$ resulta em $m = 4.69$
Exemplo Prático – Hidrograma de Nash
Dado um evento de precipitação que produz um volume de escoamento superficial de $300~\mathrm{m^3}$ e vazão de pico de $0.25~\mathrm{m/s}$, determine o tempo de pico e o hidrograma e sua propagação.
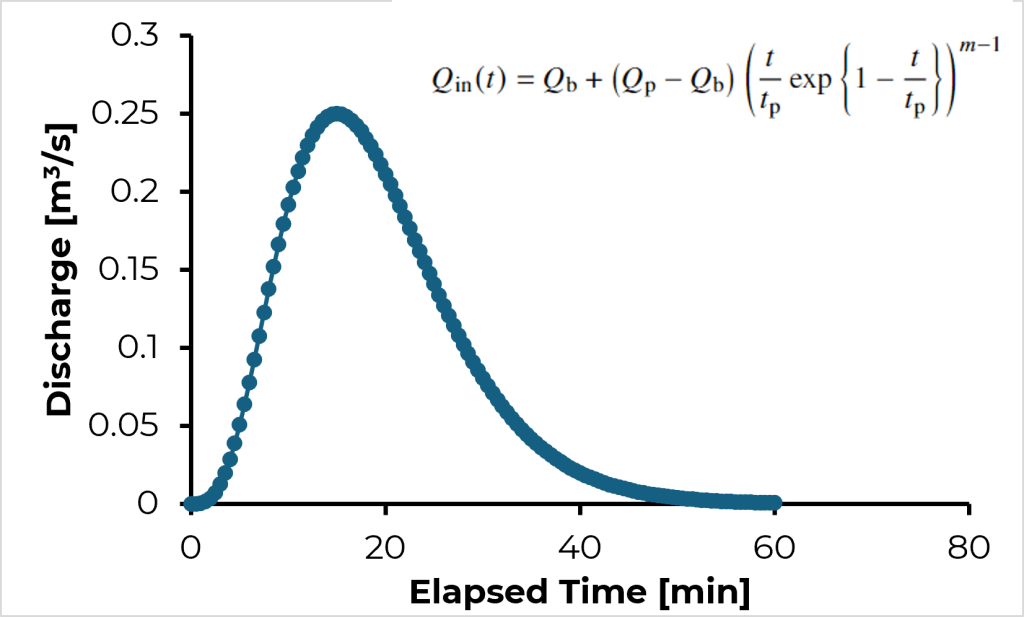
Aplicação dessa abordagem usando o Hidrograma de Nash
Técnicas compensatórias de drenagem urbana como pavimentos permeáveis, jardins de chuva ou telhados verde geralmente são dimensionados sob o foco de tratamento de água.
Assim, tipicamente seu critério de dimensionamento é baseado no armazenamento de um volume mínimo chamado de Water Quality Volume (WQV), que é aproximadamente o volume que a bacia de drenagem geraria se uma chuva de 1 polegada (25.4 mm) ocorresse.
A vazão de pico é também fácil de ser estimada. Pode-se usar o método racional para se obtê-la.
Assim, tendo apenas 2 variáveis (i.e., o volume de escoamento superficial e a vazão de pico) é possível delimitar um hidrograma que tem exatamente esse volume e essa vazão de pico.
Essa equação também é bem fácil de ser replicada e não requer processos complexos como convolução, por ex.
Baixe a planilha clicando aqui.
