Ajuste de Curvas IDFs – Hidrologia Estatística
Ajuste de Curvas IDF são um dos problemas mais corriqueiros na engenharia hidrológica.
Curvas IDF relacionam intensidade de precipitação $(i)$, duração ($t_d$) e frequência ($\mathrm{TR}$).
Qualquer relação que escreva $i = f(TR,t)$ com um determinado grau de acurácia é válido como formato de curva IDF.
Alguns tipos comuns de curvas IDF são os tipos $\texttt{Talbot}$, $\texttt{Sherman}$, ou com logaritmos de base 10 ou natural.
$$i = \frac{a\mathrm{TR}^b}{t_d+c}~~\mathrm{(Talbot)} $$
$$i = \frac{k\mathrm{TR}^a}{(b + t_d)^c}~~\mathrm{(Sherman)} \tag{1}$$
$$i = k_1 t_d^{k_2} + k_3 t_d^{k_4}\Bigl(k_5 – \mathrm{ln}(\mathrm{ln} \frac{\mathrm{TR}}{\mathrm{TR} – 1})\Bigr)~~\mathrm{(Log-fitted)}$$
Um dos tipos mais comuns e aplicados é a curva IDF tipo Sherman.
Softwares como o ${\href{http://www.gprh.ufv.br/?area=softwares}{Plúvio}}$, da UFV, utilizam esse formato, facilitando o uso em todo Brasil.
Passo a Passo do Ajuste de Curvas IDF
Basicamente, uma forma geral aplicada para determinar os coeficientes da eq. de chuvas intensas pode ser pensada da seguinte forma:
- Ajustar os valores de máximos anuais para tempos de retorno de 1, 2, 5, 10, 25, 100, 200, 500, 1000.
- Desagregar valores diários de precipitação para valores sub-horários de 5, 10, 15, 20, 25, 30, 60, 360, 480, 600, 720 e 1440 minutos
- Encontrar os parâmetros $k,~a,~b$ e $c$ de modo a minimizar uma função de erro entre valores modelados com os coeficientes e desagregados.
Ajuste de Curvas IDF tipo Sherman
Os valores escolhidos para as durações e tempos de retorno analisados interferem na qualidade do ajuste.
Assim, se, por exemplo, você tem o objetivo de fazer uma IDF que mais se ajusta a dados com tempo de retorno menores, você usa mais tempos de retorno baixos para ajustar a curva.
O contrário é verdadeiro.
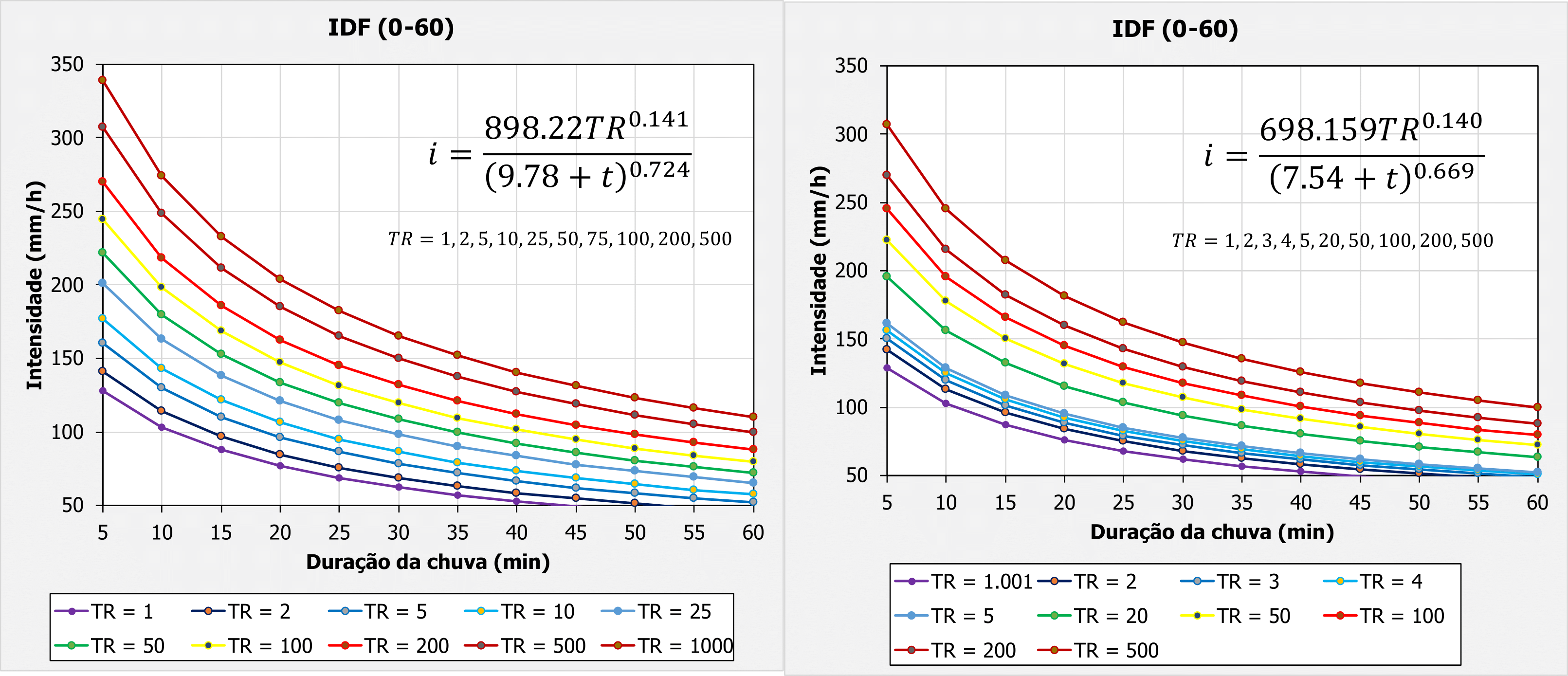
Vamos imaginar que consigamos montar uma tabela relacionando durações na primeira coluna, e valores de intensidade de precipitação para cada tempo de retorno nas outras colunas
Para calcular intensidades de precipitação, basta dividir a precipitação diária desagregada ($P^*$) para valores sub-diários pela duração ($t_d$).
$$ i(t_d) = \frac{P^*}{t_d}$$
Assim, uma matriz $\mathbf I_p$ é formada a partir das desagregações de cada $i^{t_n \times TR_n}$, onde $n$ é a duração sub-diária analisada
Podemos fazer a diferença quadrática entre cada elemento das linhas e colunas de $\mathbf I_p$ com valores modelados usando a Eq. 1 e definir um erro
A função de erro pode ser calculada, portanto, como
$${\mathrm{Erro~Quadrático~Médio}} = \frac{1}{N} \sum ({I_p} – {I_m})^{2}$$
onde N é o número total de dados de chuva usados na análise. $I_p$ e $I_m$ são matrizes que construímos para diversos tempos de retorno e durações de chuva.
Exemplo 1)
Construa a curva IDF a partir dos dados de precipitação diária máxima anual. Utilize o método de Gumbel e os coeficientes de desagregação da CETESB.
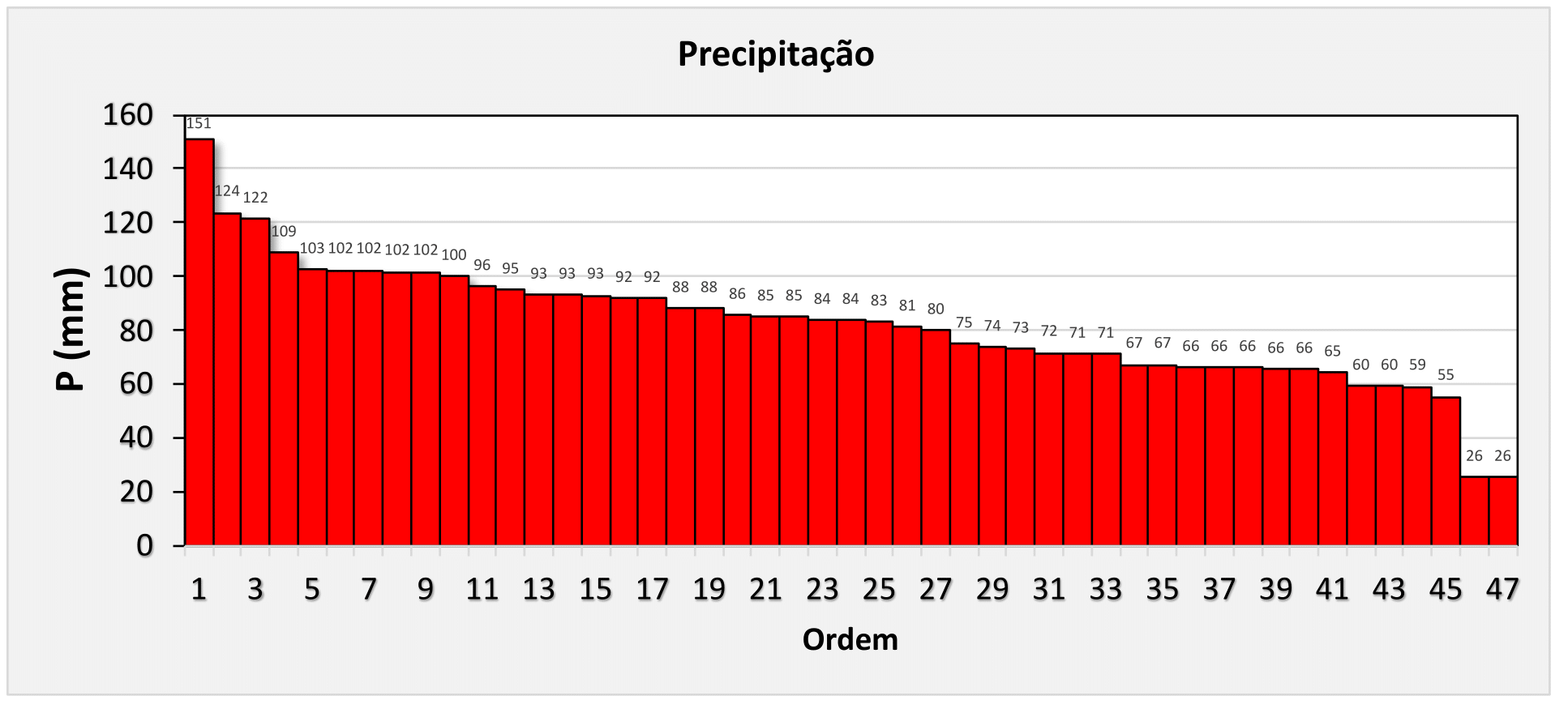
Agora que já aprendemos nos exemplos anteriores dos artigos passados como ajustar modelos de distribuição Gumbel, Normal e Log-Normal, podemos elaborar um histograma de frequências onde comparamos os dados observados com os dados modelados pelas distribuições teóricas, de modo que:
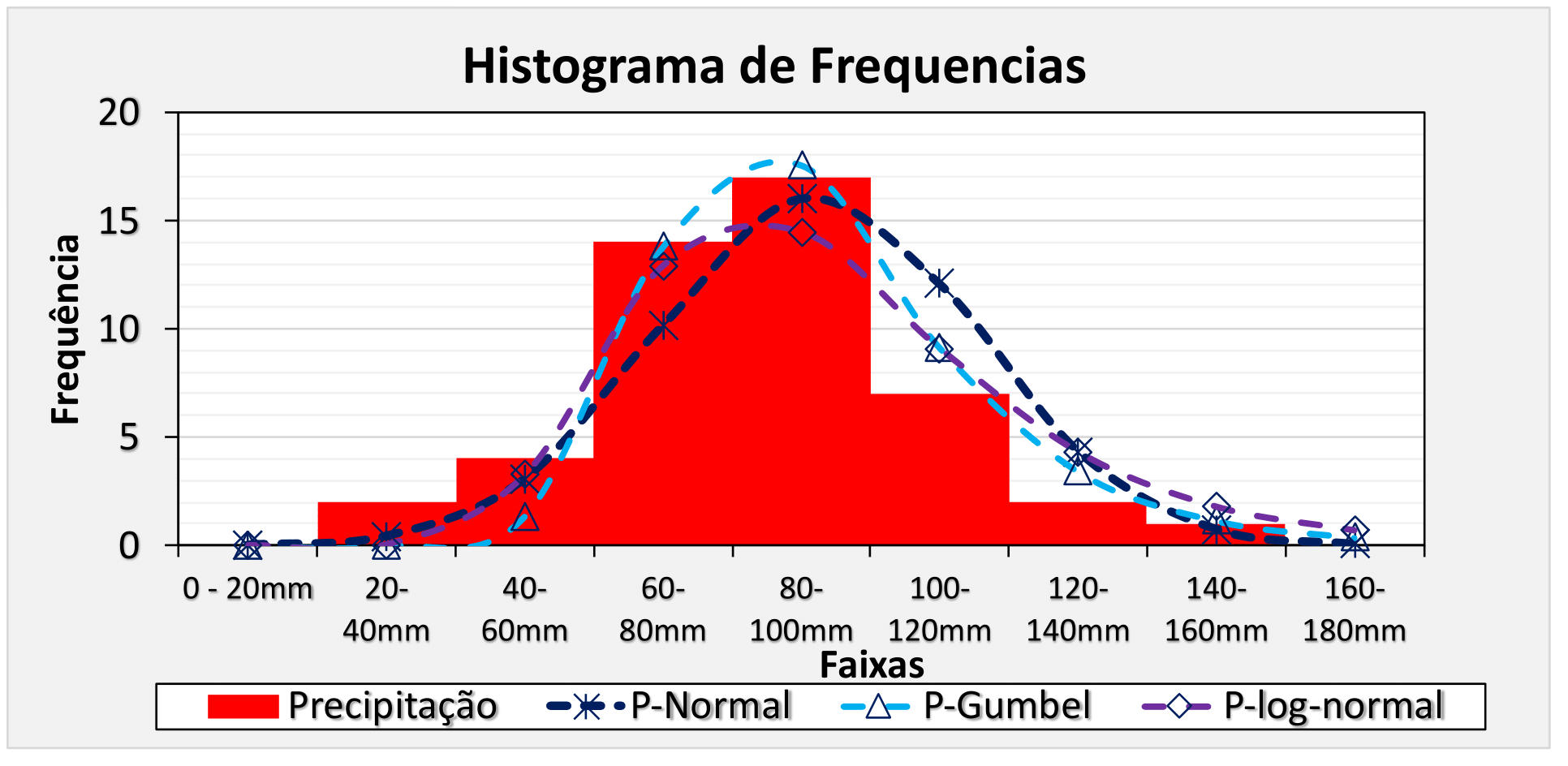
Perceba que nenhuma distribuição fica perfeita na amostra. Porém, a distribuição Gumbel e Normal parecem ser um pouco mais adequadas.
No entanto, a distribuição normal superestima mais dados extremos que a distribuição de Gumbel.
A escolha de uma ou outra para análise pode ser feita usando Testes de Aderência.
Por simplicidade, vamos adotar Gumbel como a distribuição de probabilidades teórica que modela a variável aleatória.
Resumo das Etapas
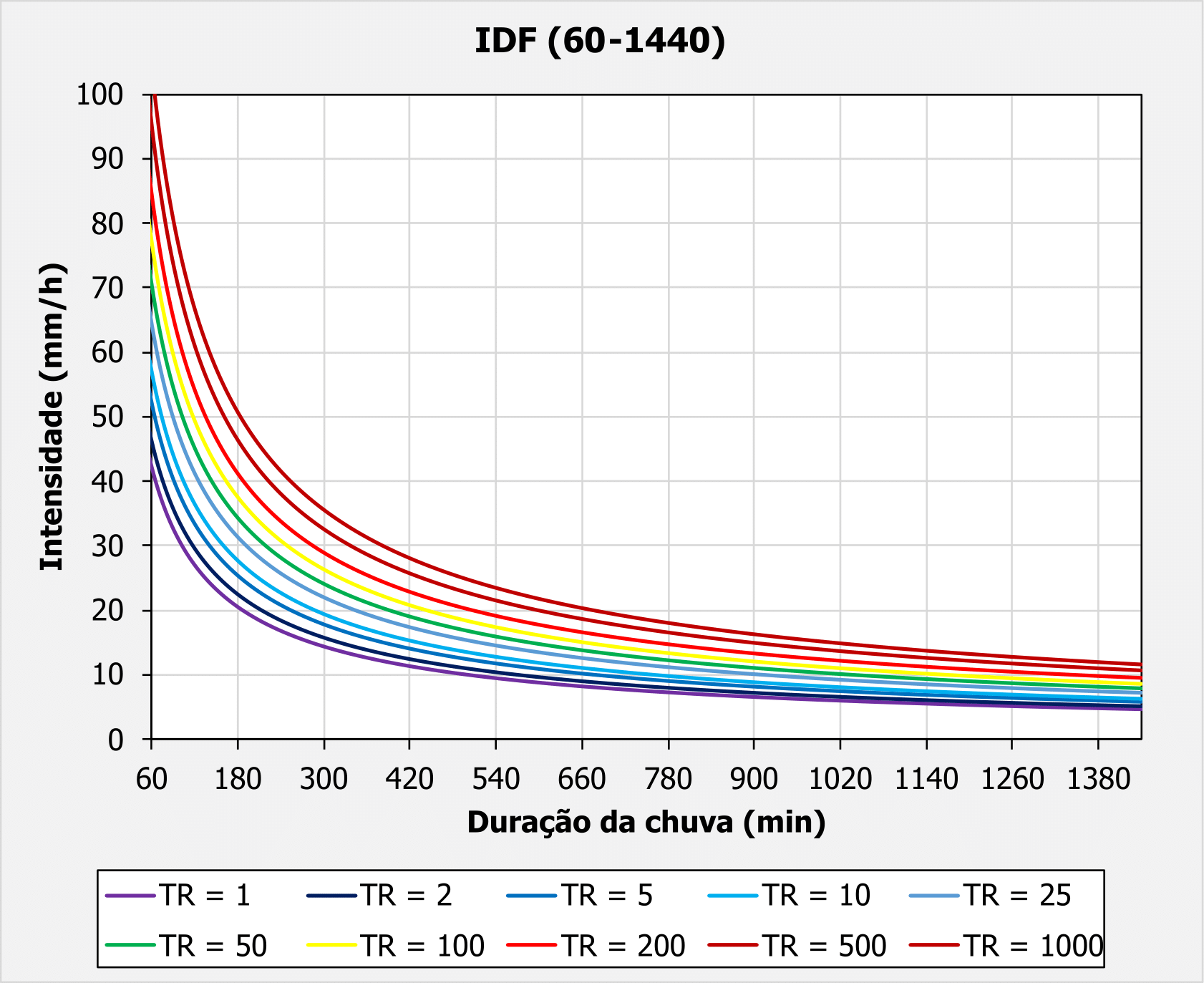
- Calcular a precipitação diária para os tempos de retorno escolhidos. Nesse exemplo, $\mathrm{\mathbf{TR}} = [1,~2,~5,~10,~25,~50,~100,~200,~500,~1000]^T$
- Desagregar valores de precipitação para valores sub-diários. Nesse exemplo, $t_d(\mathrm{min}) = [5,~10,~15,~20,~25,~30,~60,~360,~480,~600,~720,~1440]^T$ usando os coeficientes de desagregação da CETESB.
- Adotar valores de $k,~a,~b$ e $c$ de e calcular $i$ com a Eq. 1 para cada tempo de retorno e duração.
- Calcular o erro entre os valores desagregados ($\mathbf I_p$) e modelados ($\mathbf I_m$) usando o erro quadrático médio
- Repetir o processo alterando $k,~a,~b$ e $c$ até o erro ser menor que a tolerância ou minimizar o erro alterando $k,~a,~b$ e $c$ via problema de otimização usando o solver, por exemplo.
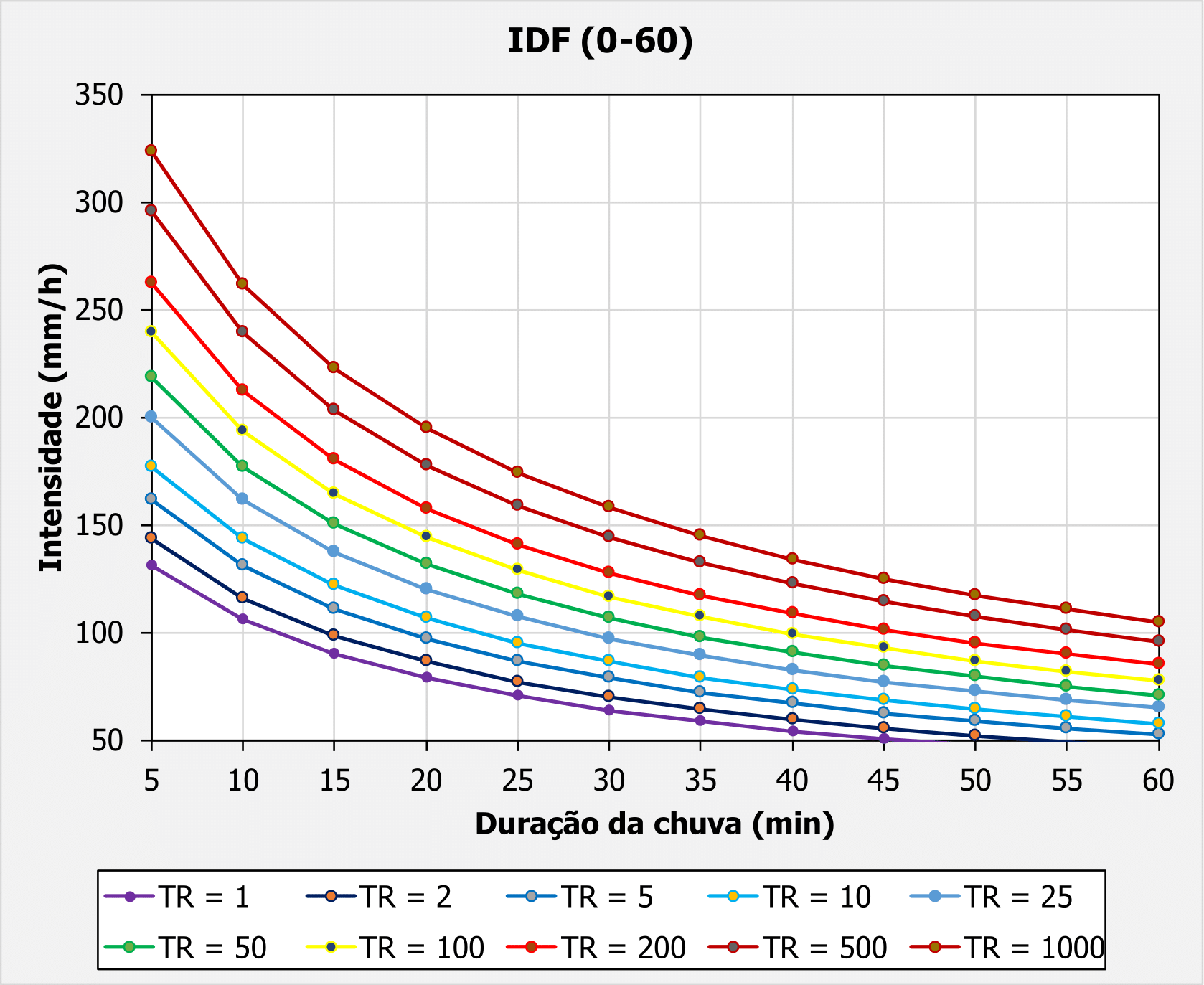
Conclusão
Com esse roteiro básico temos uma ferramenta importante e poderosa para ajustar curvas IDF para qualquer série de dados de precipitação máxima anual.
Se você quiser se aprofundar mais e entender os meandros e nuâncias mais específicas da Hidrologia Estatística, recomendo fazer o meu curso completo onde resolvo exemplos passo a passo e explico detalhes importantes sobre Hidrologia Estatística.

Mestre e Doutor em Engenharia Hidráulica e Saneamento pela USP – São Carlos. Vencedor do Prêmio Tese Destaque de teses da USP (2024) e autor de diversos artigos nacionais e artigos internacionais. Pesquisador de Pós-Doutorado II na University of Arizona, Department of Hydrology and Atmospheric Sciences, USA. Engenheiro civil formado pela Universidade Estadual de Maringá. Fundou o canal Engenheiro Planilheiro em 2017 após perceber que suas planilhas poderiam dar uma contribuição real para diversos engenheiros, arquitetos e profissionais da área, contando com mais de 100 mil planilhas já baixadas e diversos clientes atendidos no Brasil e no mundo.

