Teste de Aderência – Hidrologia Estatística

Muito bem. Até agora aprendemos alguns métodos de distribuição empíricos e teóricos, mas ainda não sabemos, de maneira convincente, se as distribuições escolhidas para representar a amostra são de fato representativas.

Para isso, testes de aderência são uma ferramenta importante.

Na literatura, vários testes são disponíveis, muitos baseados em conceitos estatísticos.

Nesse artigo, ao contrário de métodos rebuscados, vamos discutir sobre alternativas práticas e relativamente simples para se avaliar se uma distribuição de probabilidades aplica-se a uma amostra, seja ela de precipitações ou de vazões, ou de qualquer outra variável aleatória.

Caso queira saber sobre métodos estatísticos como o método de Kolgomorov-Smirnov, recomendo ler esse artigo científico onde falo mais sobre.

Na planilha completa de Curvas IDF esse método também é programado e usado para avaliar a aderência dos métodos de distribuições de probabilidade; então, caso seu estudo precise dessa análise, a planilha também pode lhe atender.

Mas afinal, como podemos testar, de maneira simples, se uma distribuição de fato é representativa da amostra?

Primeiro vamos conceituar o que é uma curva CDF (Cumulative Distribution Frequency) ou Curva de Distribuição Acumulativa.

Ela é, uma função normalizada, que fornece, para cada valor da variável aleatória, a probabilidade de acumulada até o ponto da amostra testada.

Vamos imaginar a distribuição apresentada na figura abaixo:

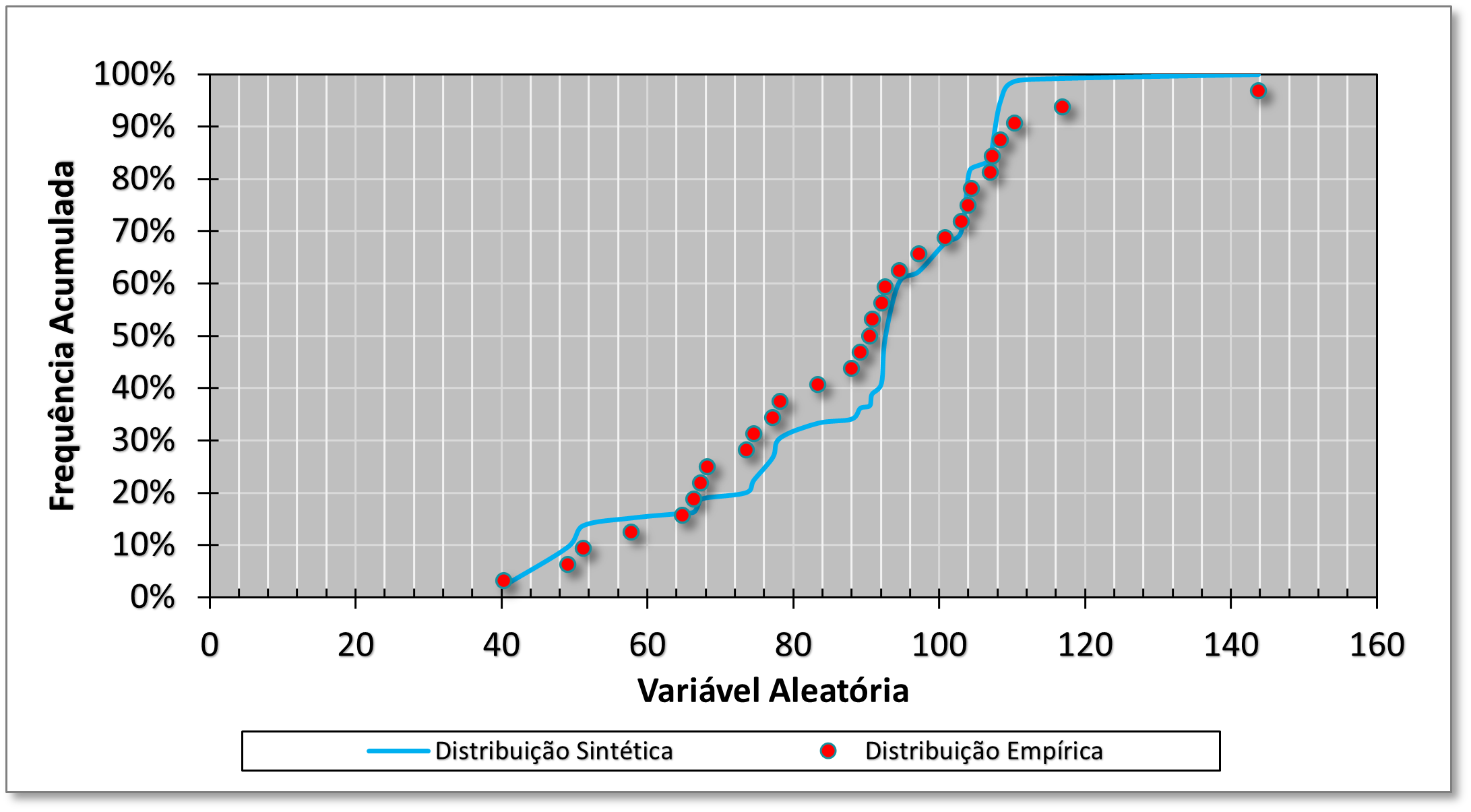
A linha azul representa uma distribuição que estamos tentando checar se ela se adequa ou não aos valores observados, assumidos por uma distribuição empírica.

A título de exemplo, vamos imaginar que a linha azul seja a CDF da distribuição de Gumbel e os pontos em vermelho os valores de frequência acumulada usando a fórmula de Weibull.

É difícil saber exatamente se uma distribuição representa a outra; visualmente parece que sim; mas há métodos estatísticos para testar essa hipótese que, de novo, caso queria saber, recomendo ler esse artigo.

Para nós, de maneira prática aqui, parece que ambas distribuições representam mais ou menos a mesma coisa.

Qual o passo a passo para chegar nisso?

• Ordenar os valores do maior para o menor
• Calcular a frequência acumulada (i.e., $ 1 – \mathrm{Prob}(x \leq x_m)$) para a distribuição empírica e teórica
• Plotar ambas frequências acumuladas
• Verificar se há alguma diferença muito, isto é, um desvio absoluto, entre ambas. Se não for muito grande, provavelmente ambas distribuições podem representar bem o problema.
• Via de regra, diferenças de até 15% são toleráveis

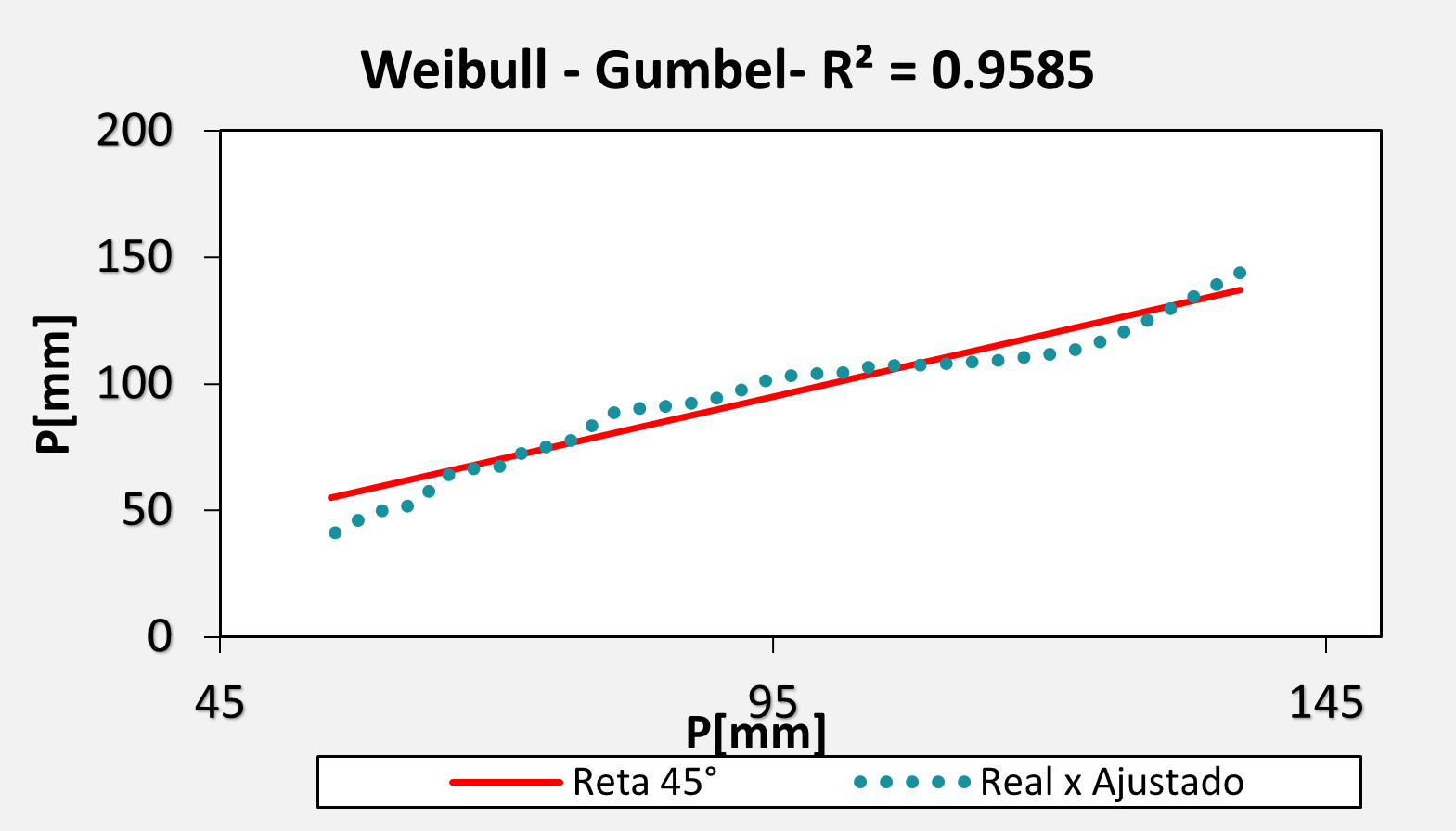
Alternativa usando o $R^2$

Para uma série de dados, se você tiver os valores observados e os valores modelados com a distribuição teórica, você simplesmente pode calcular o coeficiente de determinação.

Via de regra, valores acima de 0.95 são bons ajustes.

Para calcular o coeficiente de determinação você pode usar as funções que o próprio Excel tem ou usar a ferramenta de ajuste de reta e pedir para apresentar o $R^2$ na figura.