Estudo Hidrológico e Hidráulico de Pontes

Nesse artigo vamos determinar a cota mínima que uma ponte deve ter para suportar uma cheia de um tempo de retorno conhecido.

Aqui apresentaremos passo a passo a metodologia de como fazer aplicando-a em um exemplo.

1 – Definição do problema

Uma licitação deverá ser elaborada para a construção de uma ponte na seção exutória de um rio, em uma determinada bacia hidrográfica. 

Assim, solicita-se um estudo hidrológico e hidraúlico para determinação da cota mínima da ponte para um tempo de retorno de 100 anos.

1.1 – Dados de Entrada

O Estudo Hidrológico e Hidráulico de Pontes necessita de diversos dados que serão apresentados aqui nesse texto.

Devemos determinar parâmetros da curva de intensidade duração e frequência (IDF) da região.

Seguindo, parâmetros da bacia hidrográfica devem ser levantados e finalmente dados da batimetria do rio na seção exutória também devem ser levantados.

1.1.1 – IDF

Os parâmetros da curva IDF tipo Sherman são apresentados abaixo:

K = 3450

a = 0.225

b = 58.409

c = 0.947

1.1.2 – Bacia Hidrográfica

Além disso, o Estudo Hidrológico e Hidráulico de Pontes requer dados relativos à bacia hidrográfica, apresentados abaixo:

A = 60 km2 (área de drenagem)

L = 5 km (comprimento do talvegue princpal)

i = 0.015 m/m (declividade média do talvegue)

n = 0.035 (coeficiente de rugosidade médio da bacia)

%Aimp = 10 (porcentagem de área impermeável diretamente conectada na bacia)

1.1.3 – Uso e Ocupação

Diversos tipos de uso e ocupação do solo são relacionados em função da área de drenagem respectiva de cada uso.

Dados abaixo mostram como diversos usos e ocupação do solo são presentes na bacia

CN1 = 61 (4%)

CN2 = 59 (15%)

CN3 = 66 (40%)

CN4 = 71 (41%)

1.1.4 – Vazão de Base

Nesse projeto, vamos considerar uma vazão de base constante de $q_b = 5 m^3/s $

Esse valor será acrescentado na vazão de pico do hidrograma.

1.1.5 – Seção exutória

Um levantamento feito na seção exutória da bacia é utilizado para determinar a curva cota-área da seção, bem como a rugosidade média de cada sub-trecho.

 

Ponto	Cota (m)	Trecho	Manning	Distância Horizontal (m)
1	103.425	1 – 2	0.03	5.140
2	103.205	2 – 3	0.03	4.860
3	101.09	3 – 4	0.03	2.660
4	100.15	4 – 5	0.03	4.125
5	100.033	5 – 6	0.03	3.355
6	99.576	6 – 7	0.03	3.405
7	97.043	7 – 8	0.03	5.215
8	97.057	8 – 9	0.03	5.610
9	97.366	9 – 10	0.03	5.625
10	99.964	10 – 11	0.03	6.180
11	100.667	11 – 12	0.03	3.820
12	101.366	12 – 13	0.03	4.665
13	102.967	13 –	0.03

 

O talvegue foi estimado com declividade média de = 1.5%

2 – Resultados – Estudo Hidrológico e Hidráulico de Pontes

Os resultados mínimos necessários para a elaboração de Estudo Hidrológico e Hidráulico de Pontes são apresentados aqui adiante.

2.1 – Chuva de Projeto

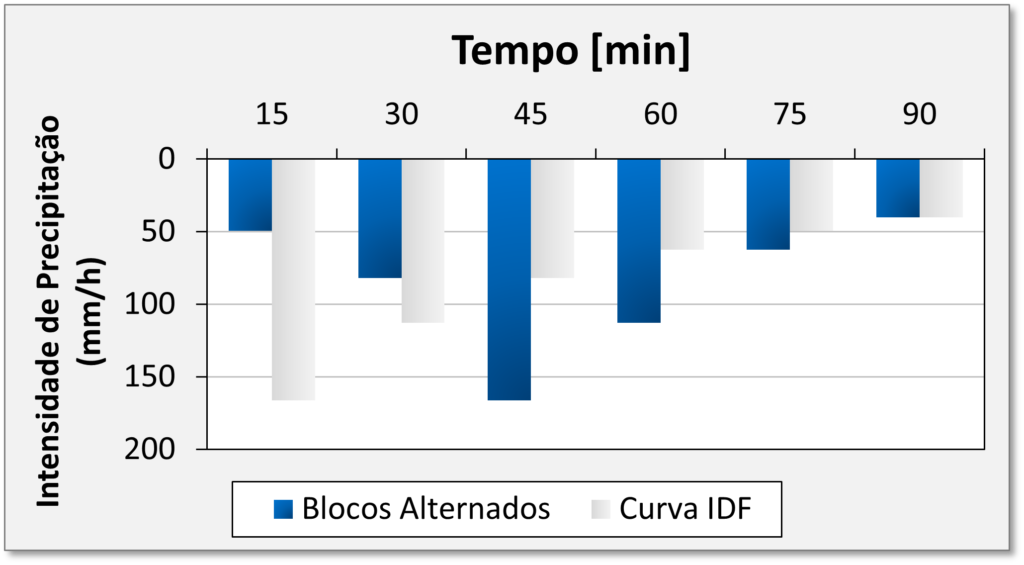
2.2 – Curve Number Medio

Fazendo-se a média ponderada entre todos os curve-numbers e áreas adotadas, tem-se que:

$$
CN = \sum_{i = 1}^n A_i . C_i
$$

Onde $n$ representa o número de tipos de uso e ocupação e $A$ representa a área de drenagem de cada um destes.

Portanto, o $CN$ médio é de 66.79.

2.3 – Tempo de Concentração

O tempo de concentração é necessário para determinar a duração mínima que a chuva terá no projeto.

Desse modo, sua estimativa levou em conta diversas fórmulas e os resultados são apresentados no gráfico abaixo:

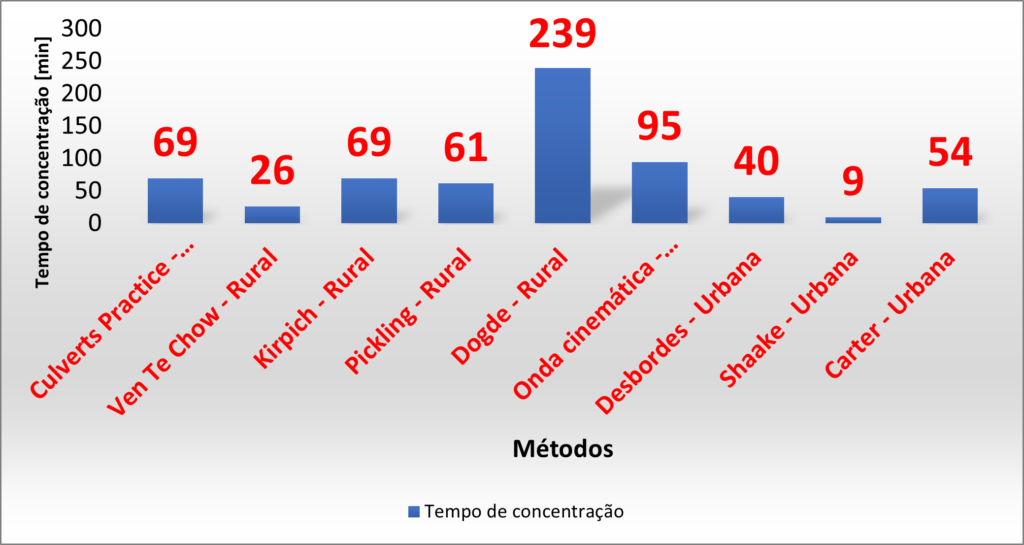
Os resultados apresentados pelos métodos acima indicam que não seria um absurdo adotar um tempo de concentração de 90 minutos para essa bacia.

Portanto o tempo de concentração adotado nesse projeto é de 90 minutos.

2.4 – Hidrograma de Projeto

Finalmente, tendo em posse o curve-number médio, o hietograma, a área da bacia e o tempo de concentração, podemos determinar o hidrograma de projeto usando a teoria do hidrograma unitário do método SCS.

Alguns parâmetros precisam ser calculados como:

$S = 25400/CN – 254 = 126 \text{mm}$

$I_a = 0.2*S = 25 \text{mm}$

$t_L = 0.6*t_c = 54 \text{min}$

$t_R / 2 = 7.5 \text{min}$

$t_p = t_L + t_R = 61.5 \text{min}$

$t_b = 2.67*t_p = 164.2 \text{min}$

Os resultados gerais da simulação feita pelo método SCS são apresentados na tabela abaixo, em excessão da convolução do hidrograma que foi omitida.

t [h]	Passo	Tempo [min]	Precipitação [mm/h]	Precipitação [mm]	Precipitação acumulada [mm]	Chuva Excedente – acum [mm]	ΔR [mm]	Vazão [m³/s]
0.25	1	15	49.3	12.32	12.32	0.00	0.00	5.00
0.5	2	30	81.8	20.44	32.76	0.42	0.42	5.00
0.75	3	45	166.3	41.58	74.34	13.73	13.31	6.25
1	4	60	112.6	28.16	102.50	29.31	15.57	47.03
1.25	5	75	62.3	15.58	118.08	39.32	10.01	134.07
1.5	6	90	40.1	10.02	128.10	46.15	6.83	250.82
1.75	7	105	0.0	0.00	0.00	0.00	0.00	386.01
2	8	120	0.0	0.00	0.00	0.00	0.00	461.80
2.25	9	135	0.0	0.00	0.00	0.00	0.00	464.33
2.5	10	150	0.0	0.00	0.00	0.00	0.00	417.68
2.75	11	165	0.0	0.00	0.00	0.00	0.00	337.64
3	12	180	0.0	0.00	0.00	0.00	0.00	255.58
3.25	13	195	0.0	0.00	0.00	0.00	0.00	173.62
3.5	14	210	0.0	0.00	0.00	0.00	0.00	95.93
3.75	15	225	0.0	0.00	0.00	0.00	0.00	42.52
4	16	240	0.0	0.00	0.00	0.00	0.00	15.29

Onde $\Delta R$ é a precipitação efetivia que houve em cada

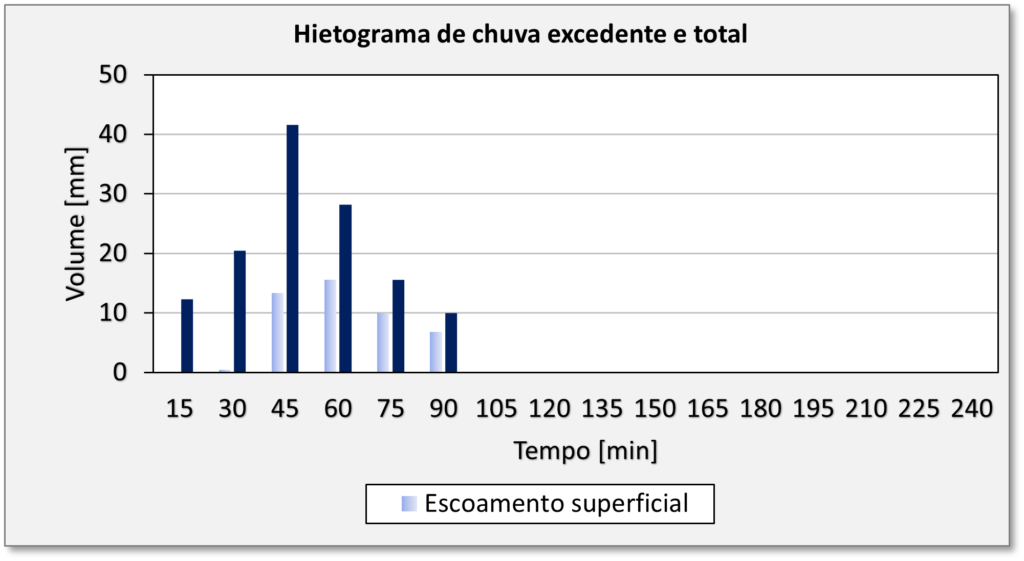
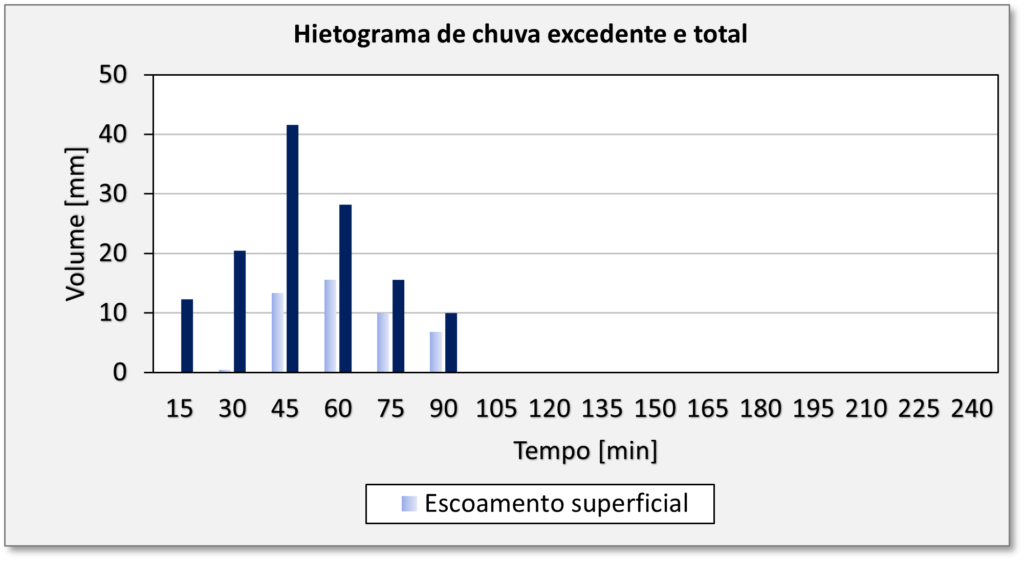
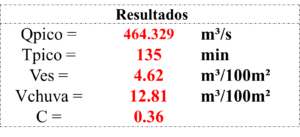
Os resultados mostrados na tabela anterior demonstram que a vazão de pico ($Q_p$) é de cerca de 464 m3/s, enquanto que o volume de escoamento superifial é de aproximadamente 4.6 m3 a cada 100 m2 da bacia hidrográfica.

Isso significa que se você captar a água em uma área de 100 m2, você seria capaz de encher uma piscina de 4600 L.

2.5 – Cota de projeto para TR = 100 anos

De posse de todos os dados anteriores provenientes do estudo hidrológico de determinação de máximas vazões de pico, o próximo passo agora é determinar qual a cota que essa vazão geraria na seção exutória em estudo.

Assim, uma maneira simplificada e prática muito utilizada nesse caso é assumir o escoamento em regime permanente e uniforme para a seção exutória

Desse modo, dado a vazão de pico estimada em projeto, basta determinar iterativamente a cota de projeto que ela geraria.

Essa cota é o resultado primordial do Estudo Hidrológico e Hidráulico de Pontes.

2.5.1 – Modelo Hidráulico

De maneira geral, queremos resolver a equação de Manning para diversos coeficientes e diversas seções, tal que:

$$Q_{tot} = Q_{1} + Q_{2} \dots + Q_{n}$$

onde n representa o número de seções que uma seção transversal é sub-dividida

Para calcularmos cada uma das sub contribuições, podemos aplicar a equação de manning.

$$Q_i = \frac{1}{n_i}A_i(h).R_{h,i}(h)^{2/3}.S_0^{1/2}$$

Onde $A_i$ é a área de seção transversal da seção i, $R_h$ seu raio hidráulico e $S_0$ sua declividade, assumida como a declividade de fundo.

2.5.1.1 – Perímetro Molhado

Dado uma seção i definida pelas cotas dos pontos $i$ e $i + 1$ (andando da esquerda para direita) e sabendo-se a distância horizontal entre esses dois pontos assumida como $d_i$, o perímetro molhado dessa seção é justamente a hipotenusa do triângulo formado pelas duas cotas verticais juntamente com a distância horizontal, de modo que:

$$P_i = \sqrt{d_i^2 + (\text{abs}(C_i – C_{i+1}))^2}$$

Onde $C_i$ representa a cota levantada no ponto $i$.

2.5.1.2 – Área Molhada

Dada a mesma sub-seção do item anterior, a área molhada pode ser estimada como a área de um trapézio.

Vamos assumir que na seção transversal chegue um nível d’água $NA$, tomado em relação à uma referência igual a referência das cotas da seção.

A área molhada que uma sub-seção que vai do ponto $i$ ao ponto $i+1$ é tal que:

$$A_i = (NA – C_i)d_i + (C_i – C_{i+1})\frac{d_i}{2}$$

Desse maneira, naturalmente observa-se que se o nível d’água for menor que a menor cota da seção, não há vazão nesse sub-trecho.

Contudo, caso o nível d’água esteja em um valor entre as duas cotas que determinam uma seção, significa que será necessário fazer uma interpolação dos dados para determinar com precisão qual a área e perímetro molhado.

2.5.1.3 – Raio Hidráulico

O raio hidráulico de uma sub-seção pertencente a uma seção transversal em estudo é, em linhas gerais, a razão entre a área molhada e o perímetro molhado, de modo que:

$$R_{h,i} = \frac{A_i}{P_i}$$

2.5.1.3 – Vazão Total

Dados as fórmulações de área molhada, perímetro molhado e raio hidráulico, podemos escrever uma equação mais generalista para a vazão total, de tal sorte que:

$$Q_{tot} = \sum_{i=1}^{n_t}\frac{1}{n_i}.A_i(y).(R_{h,i}(y))^{2/3}.S_0^{1/2}$$

Onde $n_t$ é o número de sub-seções.

O problema que devemos resolver é justamente encontrar $y$ tal que $Q_{tot} = Q_p$.

Para isso, definimos uma função de erro $$E = (Q_{tot} – Q_{p})^2$$

Assim, minimizamos essa função alterando a célula variável que define a altura na seção ($h$).

De maneira gelral, esse problema pode ser facilmente resolvido utilizando a ferramenta do solver no Excel.

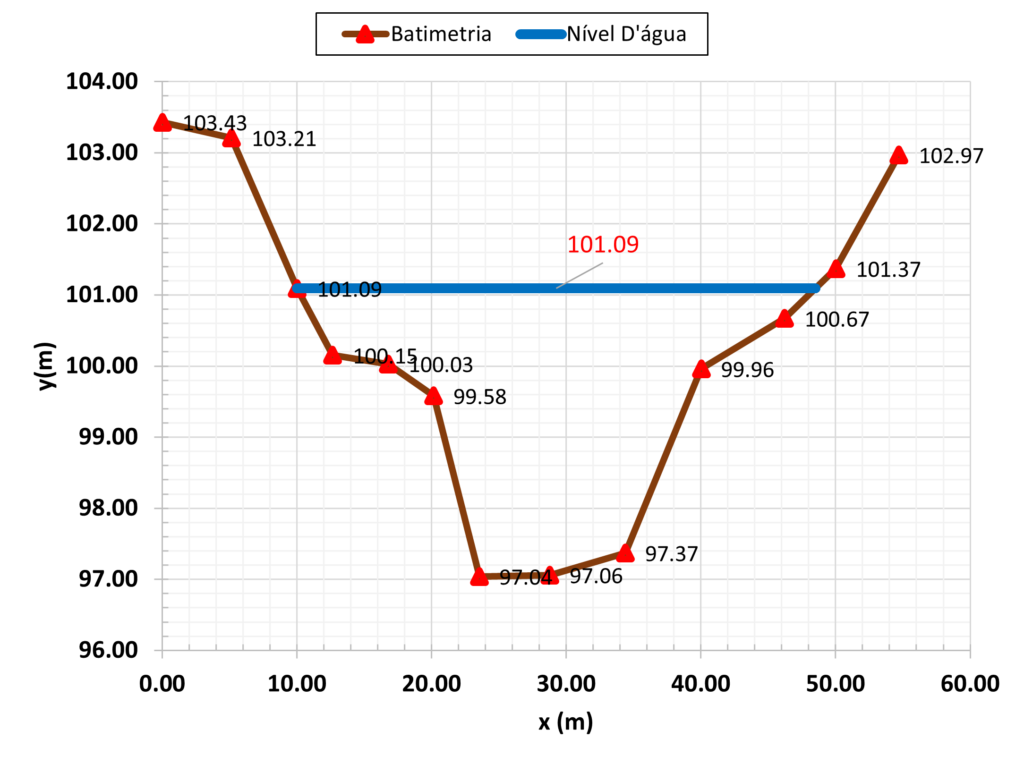
Poratanto, resolvendo o problema para os dados do projeto, temos que:

2.6 – Determinação da curva TR x Cota

Uma análise interessante do estudo de canais abertos é a determinação de curvas que mostram como variam-se as cotas máximas de projeto para diversos tempos de retorno

Nesse estudo, temos como objetivo avaliar qual a cota para tempos de retorno de 1, 2, 5, 10, 25, 50, 75 e 100 anos.

Portanto, fazemos o seguinte procedimento:

1. Alteramos o tempo de retorno e calculamos o hidrograma resultante
2. Salvamos a vazão máxima de pico
3. Resolvemos o problema da determinação da cota no canal
4. Salvamos a cota máxima de projeto
5. Repetimos o processo para todos os tempos de retorno

O resultado dessa análise é apresentado abaixo

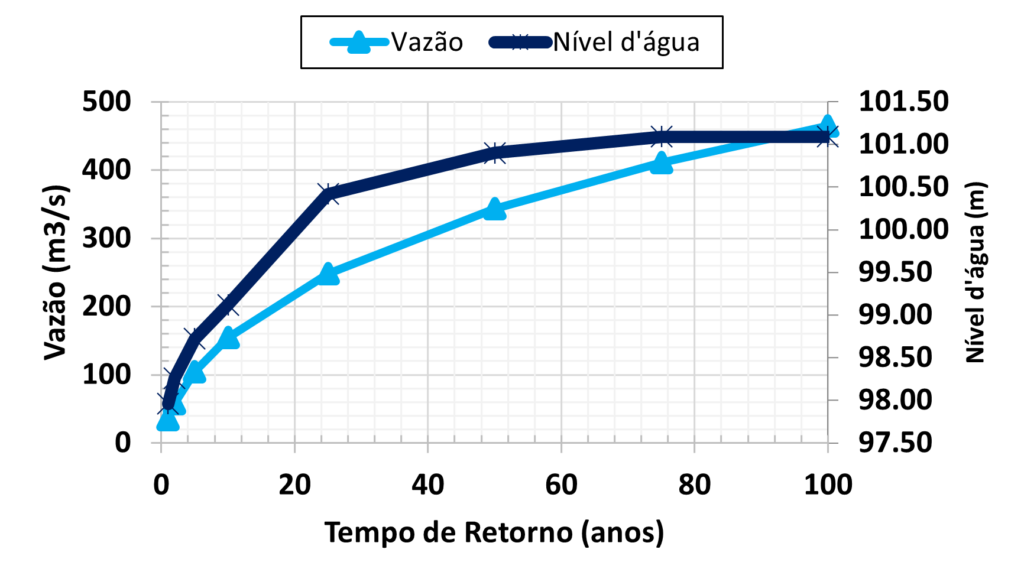
Observa-se que há uma grande variação na altura d’água, isto é, a taxa de variação da altura em relação ao tempo de retorno, próximo de TR = 10 para TR = 25 anos.

3.0 – Conclusões

Os estudos hidrológicos e hidráulicos para determinar as cotas máximas em pontes precisam ser elaborados usando métodos aplicáveis à bacia de estudo.

Além disso, nesse artigo desenvolvemos um estudo para a determinação da cota máxima de 100 anos, bem como as cotas para tempos de 1, 2, 5, 10, 25, 50 e 75 anos.

Desse modo, uma planilha 100% automática que faz esses estudos hidrológicos e hidraúlicos foi elaborada e está disponível para compra aqui ou logo abaixo:

Estudo Hidrológico e Hidráulico de Pontes