Cálculo de Redes Ramificadas
1 – Introdução
O cálculo de redes ramificadas considera como ocorrem as perdas de carga em trechos lineares de tubulação.
Geralmente, o sistema hidráulico é submetido a condições de contorno de montante e jusante conhecidas.
Essa condição de contorno pode ser o nível d’água do reservatório que abastece a rede, bem como a pressão mínima disponível no trecho mais crítico da rede.
De maneira geral, devemos garantir tanto critérios de pressão mínima (e.g., desse modo evitamos o mau funcionamento de dispositivos hidráulicos), bem como critérios de pressão máxima (e.g., redução de problemas de vazamento em tubulações).
2 – Métodos de Cálculo de Redes Ramificadas
A forma de cálculo de redes ramificadas é determinística caso saibamos as condições de contorno de montante e jusante.
Além disso, os cálculos são sequenciais e devem ser iniciados a partir do ponto mais a jusante da rede.
Perdas de carga podem ser estimadas utilizando-se equações fisicamente baseadas como a equação da fórmula universal, mas, ao mesmo tempo, também podemos usar fórmulas empíricas como as de Hazzen-Willians
2.1 – Equação da energia
Dado um trecho que sai de um ponto 1 para um ponto 2, a conservação da energia prediz que:
$$
\frac{P_1}{\gamma} + \frac{v_1^2}{2g} + z_1 = \frac{P_2}{\gamma} + \frac{v_2^2}{2g} + z_2 + \Delta H_{1-2} \tag{1}
$$
Onde $P$ é a pressão manométrica, $v$ é a velocidade média do escoamento, $z$ a cota de fundo da tubulação e $\Delta H$ a perda de carga no trecho.
A perda de carga, por sua vez, pode ser estimada com base no fator de atrito médio do trecho. Desse modo, podemos estimar a perda de carga distribuída como:
$$
J = \frac{\Delta H}{L} = \frac{f}{D} \frac{v^2}{2g} \tag{2}
$$
Onde $J$ é a perda de carga distribuída, dada em mca/m de tubulação ou expressa em m/m. As variáveis $v$ e $g$ representam, respectivamente, a velocidade média do trecho e a aceleração da gravidade, ambas em unidades do Sistema Internacional de Unidades.
2.2 – Vazões Fictícias
Há um problema na equação anterior.
A vazão em um determinado trecho não é constante.
Na verdade, cada ligação retira parte da vazão que passa por um trecho de tubulação, de modo que essa vazão é reduzida a cada lote, por exemplo.
Isso complicaria demais os cálculos caso tivéssemos de considerar cada ponto de ligação.
De modo a evitar isso, estimamos uma vazão em marcha, como se fosse uma vazão de retirada d’água a cada metro.
Em outras palavras, dados dois nós em uma rede, a diferença de vazão entre esses dois nós pode ser escrita da seguinte forma:
$$
Q_{i + 1} = Q_{i} – q_m.L_{i,i+1} \tag{3}
$$
Onde $q_m$ representa uma vazão em marcha, em unidades de L/s/m ou m³/s/m, indicando, teoricamente, o volume de vazão retirado para lotes, edificações e pontos de tomada d’água nesse trecho, por unidade de tubo.
Portanto, podemos dizer então que a vazão média (chamaremos de vazão fictícia) entre dois pontos é:
$Q_{fic} = \frac{Q_{montante} + Q_{jusante}}{2}~\text{Se } Q_{jusante}>0 \tag{4}$
$Q_{fic} = \frac{Q_{montante}}{\sqrt{3}}~\text{Se } Q_{jusante} = 0 \tag{5}$
Essa vazão fictícia é que de fato é utilizado para calcular o diâmetro da tubulação
2.3 – Diâmetros Mínimos
Os diâmetros mínimos de cada trecho de tubulação são naturalmente funções do material a ser utilizado.
De maneira geral, velocidades máximas e vazões máximas são critérios para se selecionar o diâmetro de um determinado trecho.
Assim, a tabela abaixo evidencia a relação entre cada diâmetro nominal e sua vazão e velocidade máxima correspondentes.
| DN | Vmax [m/s] | Qmáx [L/s] |
| 50 | 0.68 | 1.3 |
| 60 | 0.69 | 2.0 |
| 75 | 0.71 | 3.1 |
| 100 | 0.75 | 5.9 |
| 125 | 0.79 | 9.7 |
| 200 | 0.90 | 28.3 |
| 300 | 1.05 | 74.2 |
| 500 | 1.35 | 265.1 |
2.4 – Roteiro de Cálculo de Redes Ramificadas
- Determinar todos os trechos, comprimentos de cada trecho e cotas de montante e jusante
- Programar colunas onde são calculadas vazões de jusante, vazões em marcha, vazões de montante e vazões fictícias. Lembrar de usar a equação certa para o caso em que o ponto final é uma ponta seca (fim da rede)
- Programar equação para se determinar o diâmetro da tubulação usando a tabela anterior, em função da velocidade
- Calcular a perda de carga distribuída
- Calcular a perda de carga no trecho
- Determinar cotas piezométricas (e.g., $z + P/\gamma$) de montante e jusante
- Calcular cargas de pressão subtraindo as cotas de elevação das cotas piezométricas
- Repetir o processo para todos os trechos
O processo de cálculo é determinístico, no entanto, só será resolvido quando todos os trechos forem preenchidos.
Um dos resultados mais importantes ao final do processo de cálculo é determinar as pressões mínima e máxima em toda a rede.
Devemos garantir que todos os trechos de tubulação atendam aos critérios de pressão. Em tese, a única variável que podemos alterar é a altura do reservatório de montante.
Mas ao pé da letra, podemos alterar também o material dos tubos, alterando-se o fator de atrito.
2.5 – Determinação da Vazão de Projeto
Apesar de termos detalhado todo o processo de cálculo, ainda falta a determinação de um importante fator: a demanda de água
É esperado que a demanda de água de uma tubulação dependa da população atendida.
Além disso, ao delinearmos os projetos de tubulações, devemos ter em mente que elas devem suportar tanto variações diárias quanto sazonais.
Isto é, durante o dia, a demanda por água muda, mas há um padrão e, portanto, há um pico. Esse pico é explicado pelo fator $k_1$.
Ademais, há outro pico sazonal que geralmente ocorre em períodos de verão e de férias. Um novo fator é então adicionado, o fator $k_2$.
Juntos, $k_1$ e $k_2$ são aplicados a demanda média e então se é estimado a vazão de projeto que uma rede deve ter, de tal sorte que:
$$
Q_{projeto} = k_1 k_2 q_s.Pop \tag{6}
$$
Onde $q_s$ representa a vazão específica, expressa em m³/s/hab ou L/s/hab, e $Pop$ é a população atendida.
É importante termos em mente a vida útil do projeto. Por exemplo, se o projeto é pressuposto a ter uma vida útil de 30 anos, devemos projetar a população para o horizonte de 30 anos.
Diversos métodos existem para essa estimativa, destacam-se os métodos aritméticos, exponenciais e curvas logísticas.
3 – Exemplo
3.1 – Definição do Problema
Determine a elevação mínima de um reservatório para garantir pressões mínimas de no mínimo 15 mca numa rede ramificada apresentada abaixo:
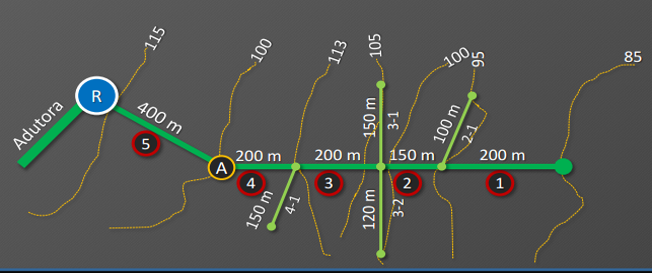
- A rede recebe água de uma adutora que leva essa água a um reservatório $R$.
- Esse reservatório distribui água para os trechos 5, 4, 4-1, 3, 3-1, 3-2, 2, 2,1 e 1
- Cada trecho tem seu comprimento e suas cotas de montante e jusante.
- A população estimada para o horizonte de projeto é de 2900 habitantes e a vazão específica é de $\mathrm{150~L/hab/dia}$.
- Coeficientes $k_1$ e $k_2$ são de 1.25 e 1.5, respectivamente.
- O fator de atrito das tubulações é estimado em 0.026.
3.2 – Esquema da Tabela para Cálculo de Redes Ramificadas
A tabela abaixo mostra como pode ser organizado os cálculos de modo a possibilitar o cálculo da rede de maneira integrada
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| Trecho | Comp. | Cota terreno (m) | Vazão (L/s) | Diâmetro | Vel. | J | Perda de Carga | Cota piez. (m) | Carga de pressão (mca) | ||||||
| Mont. | Jus. | Jus. | Marcha | Mont. | Fictícia | mm | [m/s] | m/100m | m | Mont | Jusante | Mont | Jus | ||
Dados de entrada são resumidos:

Devemos “chutar” a altura do reservatório para estabelecer as condições de pressão mínima em todos os trechos.
O cálculo da vazão em marcha $q_m$ é feito calculando-se a razão entre a vazão demandada e o comprimento total das tubulações.
3.3 – Resultados do Dimensionamento
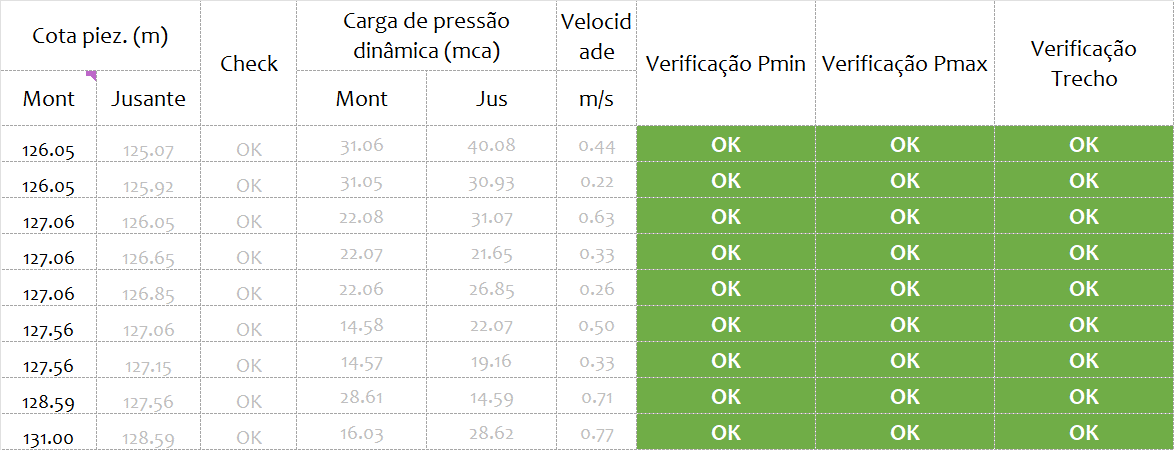
Primeiro, vejamos como os resultados estão organizados na planilha.
Os dados de entrada de cada nó da rede são organizados à esquerda, nos tópicos em vermelho.
Já os resultados de cálculo de pressões, vazões, cotas piezométricas e verificações são organizados à direita, como ilustra a figura abaixo.
Perceba também que nem todos os pontos recebem vazão em marcha. Assim, você tem a opção de selecionar quais são pontos com consumo e quais são pontos apenas de transporte de água.

Vamos inicialmente chutar a altura do reservatório em 10 metros e ver como seriam os resultados:

Perceba que alguns trechos falharam. Isso implica que, (i) ou mudamos as propriedades dos tubos (e.g., fatores de atrito) (ii) ou mudamos as condições iniciais de pressão no reservatório elevado.
Por simplicidade, mudemos a altura inicial d’água no reservatório para 16 m e refazamos os cálculos.
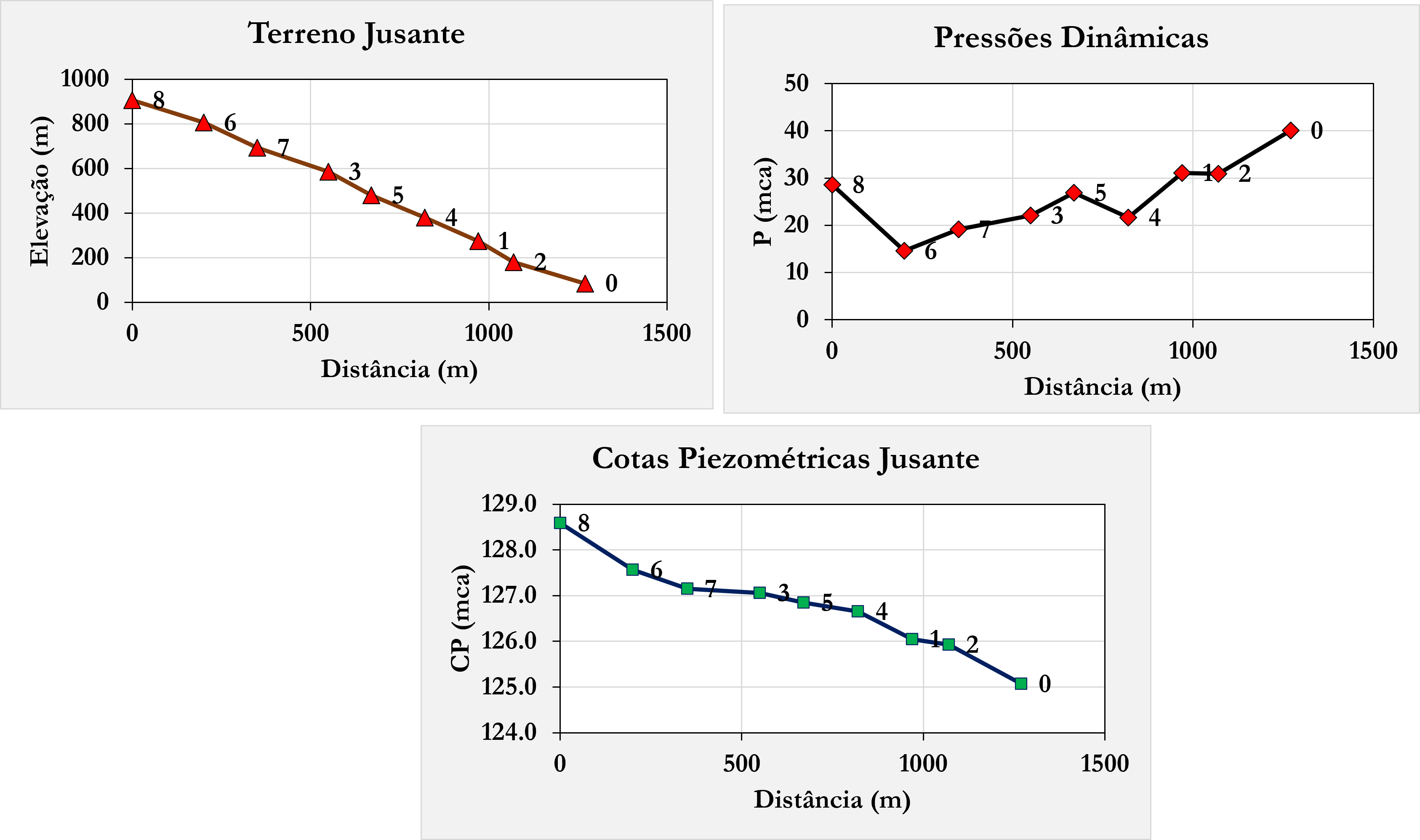
Finalmente, você pode analisar os resultados visualmente através dos gráficos automáticos que são gerados na planilha, apresentados logo abaixo:
4 – Conclusões
O cálculo de redes ramificadas é iterativo e o sistema de equações, se resolvido à mão, pode ser relativamente trabalhoso.
Além disso, recomenda-se automatizar os cálculos para determinar as condições ótimas do nível do reservatório.
Redes ramificadas, no entanto, são quase redes em série e podem estar mais submetidas a falhas.
Todo esse processo de cálculo detalhado logo abaixo é 100% automático em nosso produto, disponível em:

Mestre e Doutor em Engenharia Hidráulica e Saneamento pela USP – São Carlos. Vencedor do Prêmio Tese Destaque de teses da USP (2024) e autor de diversos artigos nacionais e artigos internacionais. Pesquisador de Pós-Doutorado II na University of Arizona, Department of Hydrology and Atmospheric Sciences, USA. Engenheiro civil formado pela Universidade Estadual de Maringá. Fundou o canal Engenheiro Planilheiro em 2017 após perceber que suas planilhas poderiam dar uma contribuição real para diversos engenheiros, arquitetos e profissionais da área, contando com mais de 100 mil planilhas já baixadas e diversos clientes atendidos no Brasil e no mundo.


3 respostas
Boa tarde, Eng. Marcus. Desculpe incomodá-lo no domingo.
Há algum tempo, conversamos rapidamente por e-mail. Talvez o amigo lembre. Também estudei em São Carlos e no momento, tenho (sou aposentado da UFRGS) algumas consutorias em andamento e preciso subsidiar meus colaboradores com alguns softwares/planilhas, com vistas a facilitar as tarefas dos mesmos.
Não encontrei o preço da planilha de dimensionamento de rede ramificada de água. Você pode me informar? Seria possível apresentar os cálculos para os diâmetros internos de PVC, PEAD e Fo.Fo.? Com orçamento das obras civis e tubulações.
Você não tem uma planilha de cálculo para redes malhadas de água(Método de Cross)? Se não, Poderia desenvolvê-la para múltiplus anéis? Qual seria o preço? O Rodrigo Porto, ex-Prof. em SCarlos tinha um software, mas precisaria ser atualizado para os computadores atuais (está disponível na versão antiga no site da Usp/SC); você poderia atualizá-lo?
Também, você não tem uma planiha de dimensionamento de redes de esgotos sanitários, com base na tensão trativa e critérios da NBR atual? Poderia desenvolvê-la? Qual seria o preço? Incluiria os orçamentos de obras civis e tubulações. Tem material antigo no site da Usp/Poli/SP.
E uma planilha ou software para cálculo do Golpe de Aríete em tubulações pelo Método das Características em linhas de recalque e adução por gravidade? Pode desenvolvê-la? Preço?
Obrigado pela sua atenção.
Abraço,
Francisco Bidone
Porto Alegre – RS Fone: (51) 9.9858.6730
Olá Francisco. Obrigado pelo contato. Acabo de te responder no e-mail com uma proposta para construção dessas planilhas! Um abraço
Marcus, bom dia!
Posso adquirir planilha para calculo de rede água?
Obs: trabalho em autarquia (Saae)
Obrigado