Perda de Solo – Método RUSLE
O processo de estimativa de perda de solo é fundamental para diversos dimensionamentos e análises, principalmente àquelas relacionadas a processos erosivos.
A erosão tipicamente se dá por efeitos da energia cinética das chuvas e do desprendimento de solo em função da velocidade do vento.
Em especial as chuvas, fatores como o fator de Erosividade R (explicado a diante), são métricas fundamentais para a estimativa das perdas de solo.
Um método simples, mas, ao mesmo tempo, relativamente acurado, é o uso da fórmula universal de perda de solo revisada, comumente chamada de RUSLE.
Caso tenha interesse nesta planilha automática e completa para a estimativa de perda de solo e tempo de assoreamento em reservatórios, entre em contato comigo, clicando aqui:
Link para baixar a planilha – https://engenheiroplanilheiro.com.br/produto/planilha-perda-de-solo/
Parâmetros Necessários
São necessários 5 parâmetros que descrevem a perda de solo, descritos logo abaixo:
A: perda anual de solo (ton/ha/ano) devido ao escoamento superficial
R: fator de erosividade (MJ/ha/(mm/h))
K: fator de erodibilidade que varia entre 0.03 a 0.79 (ton/MJ/(mm/h))
LS: fator de declividade e comprimento de encosta (adimensional)
C: fator de prática de cultura variando de 0.001 a 1 (adimensional)
P: fator de prática de cultura contra erosão que varia de 0.3 a 1.0 (sazonal)
Fórmula RUSLE – Perda de Solo
A fórmula RUSLE é dada, portanto, como:
$$
A=\text { R.K. LS.C.P } P \tag{1}
$$
Perceba que a perda de solo é diretamente proporcional a cada um desses 5 fatores, ou seja, a alteração percentual de um deles, altera na mesma proporção a perda de solo.
Assim, vamos trabalhar um pouco em cima de como podemos estimar cada um desses fatores.
Fator R – Fator de Erosividade
O fator R é um índice médio plurianual que mede a energia cinética e a intensidade da chuva para descrever o efeito da chuva na erosão laminar.
Portanto, ele é calculado levando em conta séries de precipitações médias mensais de longo termo, isto é, séries de no mínimo 20 anos.
Desse modo, quanto maior o valor de R, maior o potencial de erosão.
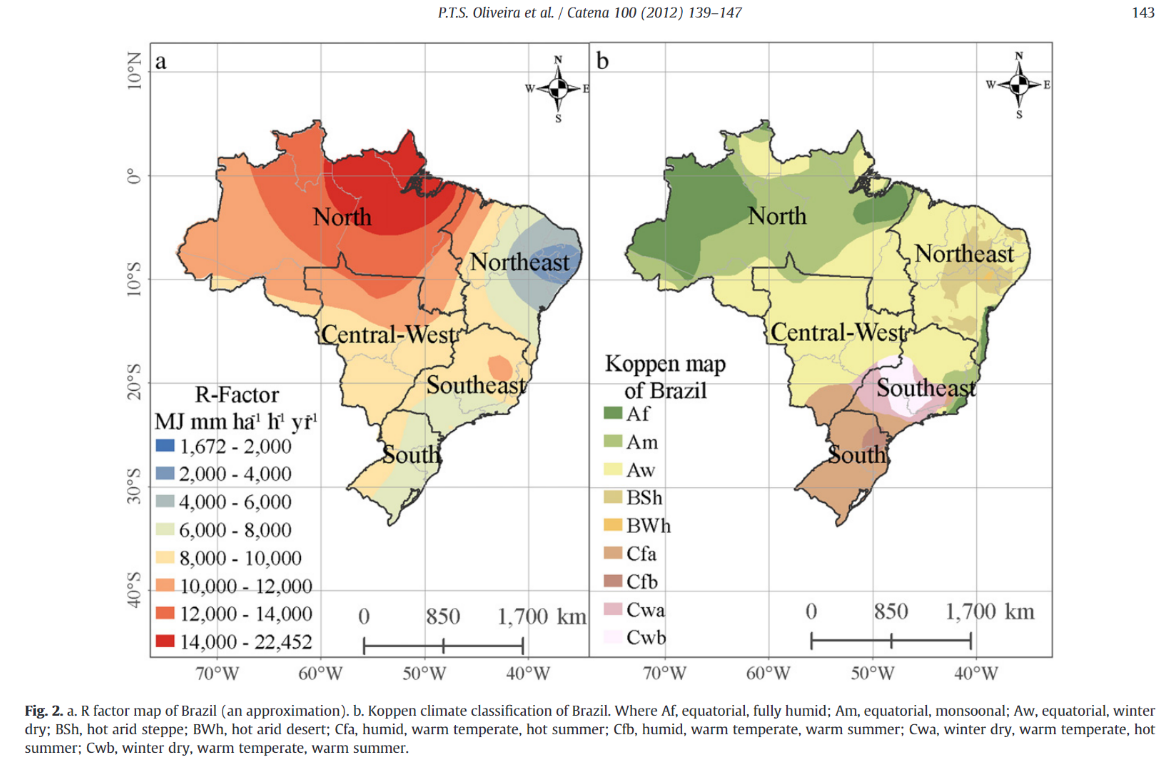
Diversos estudos apresentam valores de R para várias regiões do Brasil. Um estudo muito interessante que relaciona o valor de R para todo o Brasil é encontrado na seguinte publicação – Rainfall erosivity in Brazil: A review.
Esse artigo, de primeira autoria do prof. Paulo Tarso da UFMS, meu amigo pessoal e coautor de diversos artigos comigo, demonstra valores interpolados de R para todo o Brasil.
A seguinte figura, retirada do artigo, mostra como se varia o fator R no domínio brasileiro.
Alternativamente, o fator R é calculado da seguinte forma:
- Monta-se uma coluna com os meses de Janeiro a Dezembro.
- Entra-se com os valores de precipitação média mensal para cada mês.
- Calcula-se o fator EI30 para cada mês da seguinte forma:
$$
E I_{30}=\alpha+\beta(M F I)^\gamma \tag{2}
$$
$$
M F I=\left(\frac{p_m^2}{p_t}\right) \tag{3}
$$
$$
R=\sum\left(E I_{30}\right) \tag{4}
$$
onde $\alpha$, $\beta$ e $\gamma $variam para cada localidade e podem ser encontrados neste artigo, $EI_{30}$ é o índice de erosividade, $p_m$ é a precipitação média mensal, $p_t$ é a precipitação média anual e $R$ é o fator de erosividade calculado como a somatória de cada $EI_{30}$ de cada mês.
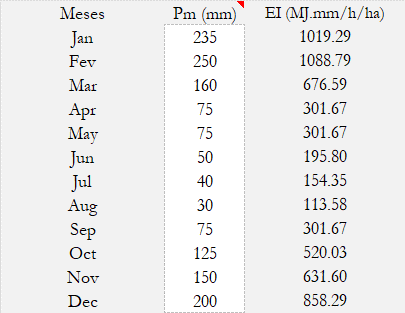
Os parâmetros $\alpha$, $\beta$ e $\gamma$ podem ser encontrados na literatura. Alguns desses valores são encontrados neste artigo.
Finalmente, o fator de erosividade R é calculado como a somatória de todos os índices de erosividade mensais para o período de 1 ano.
Fator K – Erodibilidade
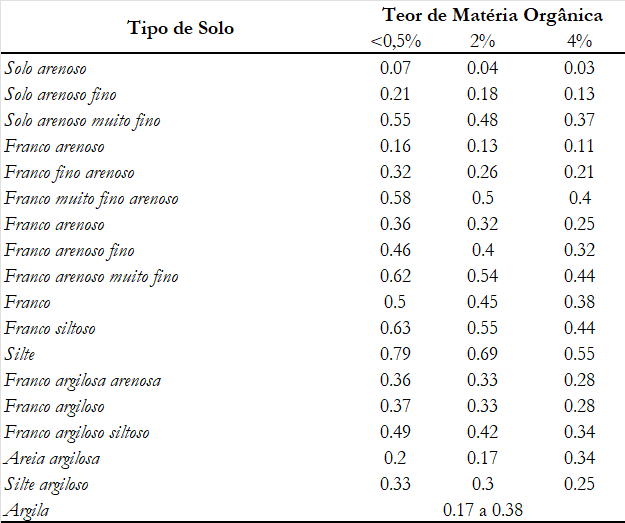
Já o fator de erodibilidade K depende primordialmente do tipo de solo e de sua quantidade de matéria orgânica.
Os valores de K podem ser estimados a partir da seguinte tabela.
Fator Geométrico – LS
Este fator considera o comprimento e a declividade da rampa onde a massa de solo é deslocada.
Apesar de as bacias hidrográficas não serem exatamente planas ou rampas, podemos aproximá-las a planos e usar o modelo RUSLE.
Nesse caso, imaginamos que a bacia hidrográfica, que conta com um canal principal, pode ser dividida em 2 planos com comprimentos e declividades conhecidos.
Assim, o cálculo total da bacia pode ser considerado como um único plano, mas, na verdade, o ideal seria considerá-la como 2 planos de declividades e comprimentos distintos.
A princípio, vamos imaginar que a bacia de estudo seja um único plano.
Se imaginarmos que esse plano tenha comprimento $Lx$ e declividade desta rampa seja $S$, o fator $LS$ para essa bacia é:
$$
L S=0.00984 . S^{1.18} L x^{0.63} \tag{5}
$$
Fator de Prática do Uso da Terra – C
Outro fator que influencia a taxa anual de perda de solo está relacionado com o modo que é feito o uso da terra.
Assim, dependendo da prática usada, diversos valores de C são atribuídos.
A tabela abaixo apresenta valores usuais de $C$ para cada uso da terra.

Fator de Prática Contra Erosão – P
As práticas de conservação podem reduzir a perda de solo.
O fator $P$ considera justamente a eficácia de técnicas de conservação na redução da perda de solo, de modo que valores abaixo da unidade representam uma prática de redução de fenômenos erosivos.
Valores usuais de $P$ podem ser encontrados na seguinte tabela:
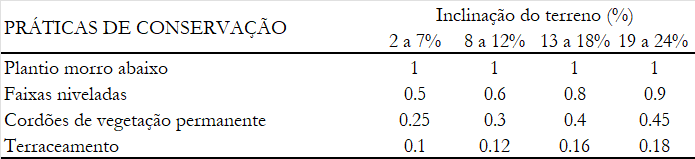
Densidade do Solo
A densidade do material granular permite estimar o volume de sedimentos mobilizados.
Duas formas podem ser usadas para estimar a densidade do solo no cálculo da perda de solo.
Primeiro, análises laboratoriais podem servir de base para estimar a densidade do solo.
No entanto, estudos apontam que esta densidade pode ser estimada da seguinte forma:
$$
\rho = 1600 + \log(d_{50}) \tag{6}
$$
Onde $d_{50}$(mm) é o diâmetro 50% retido no ensaio granulométrico e $\rho$ é a densidade do solo em $\mathrm{kg/m^3}$.
Sediment Delivery Ratio
Apesar do método RUSLE determinar o volume ou massa de solo mobilizado em média, anualmente, parte dessa massa fica ainda retida na bacia.
Desse modo, o percentual de massa que saí da bacia pode ser calculado com o fator $SDR$, de modo que:
$$
S D R=\frac{0.4724}{A^{0.125}} \tag{7}
$$
Onde $A$ é a área da bacia em $\mathrm{km^2}$.
Trap Efficiency
Finalmente, quando os sedimentos que saem de uma bacia chegam a um reservatório, parte desses sedimentos ficam depositados no fundo, e parte sai como efluente do reservatório.
Assim, o fator de trap-efficiency é calculado para estimar essa porcentagem, de modo que:
$$
T E=\left(1-\frac{1}{1+0.0021 * D * \frac{C}{A_d\left(k m^2\right)}}\right) \tag{8}
$$
Onde $D$ é um adimensional entre 0.046 e 1, usualmente adotado como 0.1, e $V_r$ é o volume do reservatório em $\mathrm{m^3}$.
Tempo para Assorear
Por fim, dado as taxas de trap-efficiency ($TE$), ($SDR$) e a perda de solo anual ($A$), conseguimos estimar o volume médio anual de sedimentos retidos em reservatórios como:
$$
V_s = A * SDR * TE \tag{9}
$$
Onde $V_s$ é o volume médio anual de sedimentos retidos no reservatório que recebe os sedimentos gerados pela bacia hidrográfica.
Assim, dado o volume anual retido $V_s$ e a capacidade do reservatório $V_r$, o tempo para assorear completamente o reservatório $T_a$ é calculado como:
$$
T_a = \frac{V_r}{V_s} \tag{10}
$$
Exemplo – Estimativa de Perda de Solo e Tempo Necessário para Assorear um Reservatório.
Estime o tempo necessário para assorear um reservatório de $\mathrm{1000~m^3}$ que recebe escoamento superficial de uma bacia de 45 ha.
Esta bacia tem solo predominantemente arenoso e fino com quantidade de matéria orgânica da ordem de 2%, ou seja, K = 0.18.
Além disso, a bacia é predominantemente composta 25% de agricultura de café, 25% de vegetação natural e 40% de plantações e 10% de áreas urbanas, resultando em um valor de C ponderado de 0.108.
Seguindo a mesma ideia, o valor de P ponderado de acordo com cada uso é de aproximadamente 0,675.
Além disso, a bacia é aproximadamente um plano de comprimento $180~m$, largura $2500~m$ e declividade da rampa de 3%, resultando em um fator
$LS = 0.948$.
O fator de erosividade é calculado assumindo $\alpha = 0$, $\beta =147.26$ e $\gamma = 0.533$ para uma série de precipitações médias mensais de $P=[235,250,160,75,75,50,40,30,75,125,150,200]^T$ de Janeiro a Dezembro.
O solo da localidade é tal que
$\mathrm{d_{50} = 0.4~mm}$, resultando numa densidade de aproximadamente $\mathrm{1600~kg/m3}$Perda_de_solo_V2.
Todo o processo de cálculo desse exemplo foi feito em planilha automática elaborada para gerar memórias de cálculo do método RUSLE.
Para ter acesso à memória de cálculo, clique aqui e baixe o PDF.



Caso tenha interesse nesta planilha automática e completa para a estimativa de perda de solo e tempo de assoreamento em reservatórios, entre em contato comigo, clicando aqui ou compre diretamente no link do produto completo disponível aqui.
Um grande abraço,
Marcus.


