Ajuste Probabilístico de Vazões Máximas – Hidrologia Estatística
Os conceitos de hidrologia estatística podem também ser abordados para o ajuste probabilístico de vazões máximas.
Similarmente a precipitação, a vazão agora é tomada como variável aleatória independente e, assumimos que ela se comporta seguindo uma distribuição de probabilidades que devemos checar e descobrir qual mais se adequa.
Para isso, nosso trabalho é: dada uma série de vazões máximas anuais $$\mathbf{Q} = Q_1,~Q_2,~\cdots Q_n$$ descobrir a distribuição de probabilidade $f(\mathbf{Q})$ que explica a distribuição observada de $\mathbf{Q}$.
Vazões Máximas Anuais
O processo de cálculo para ajustar as distribuições empíricas e teóricas é o mesmo apresentado nos artigos anteriores.
Parâmetros básicos da amostra como média e desvio padrão são usados para testar as hipóteses de distribuições teóricas.
O resultado final da análise é uma função que segue a seguinte característica:
$$ Q(\mathrm{TR}) = f(\bar{\mathbf{Q}},s(\mathbf{Q}),\mathrm{TR})$$
onde $\bar{\mathbf{Q}}$ é a vazão média da amostra e $s(\mathbf{Q})$ o desvio padrão amostral.
Exemplo – Ajuste de Vazões Máximas
Uma seção de uma ponte que escoa um rio perene tem 10 anos de observações de vazão, resultando na série de vazões máximas anuais de:
$\mathbf{Q} $=
| 2255.322 |
| 1950 |
| 1877 |
| 1560 |
| 1508.862 |
| 1492.064 |
| 1467.605 |
| 1461.927 |
| 1455 |
| 1300 |
| 1274.558 |
| 1225.949 |
| 1140 |
| 1055 |
| 950 |
| 864 |
| 863.3289 |
| 644.2573 |
| 565.1031 |
| 500 |
com valores em $\mathrm{m^3\cdot s^{-1}}$. Determine a vazão máxima anual para tempos de retorno de 2, 5, 10, 25, 50 e 100 anos para distribuições normais, log-normais e Gumbel.
Qual a discrepância de uma vazão de TR = 25 anos?
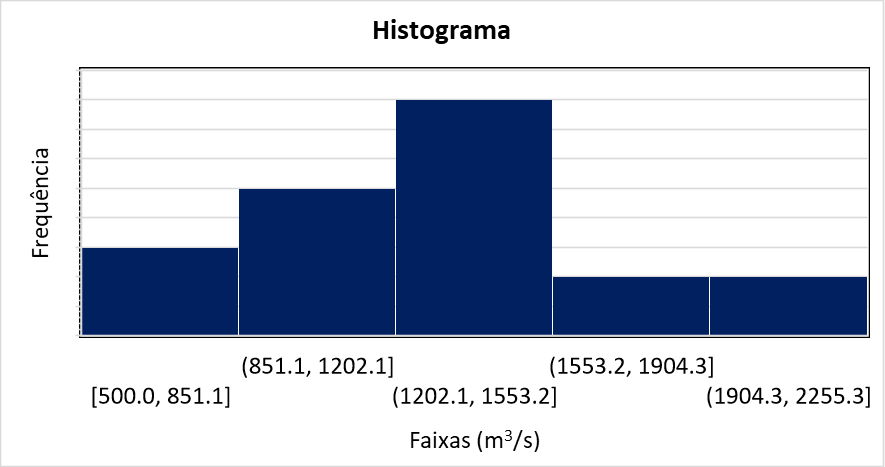
Solução:
As estatísticas descritivas da amostra são apresentadas na tabela abaixo:
| Distribuições Teóricas | ||
| Média | 1270.5 | mm |
| Desvio Padrão | 463.5 | mm |
| Media(log(Q)) | 3.073 | mm |
| Desvio Padrao (log(Q)) | 0.176 | mm |
Assim, podemos usar a formulação de Gumbel, Dist. Normal e Dist. Log-Normal para verificar quais distribuições mais se assemelham as observações.
Para isso, montamos a seguinte tabela:
| Gumbel | Normal | Log-Normal | Weibull | ||||||||
| Ordenação | Q
$\mathrm{m^3 \cdot s^{-1}}$ |
$b$ | $P(Q \geq Q_m)$ | TR | $P(Q \geq Q_m)$ | TR | log(P)
$\mathrm{m^3 \cdot s^{-1}}$ |
$P(Q \geq Q_m)$ | TR $P(Q \geq Q_m)$ | $P(Q \geq Q_m)$ | TR |
| 1 | 2255.3 | 3.30 | 0.04 | 27.67 | 0.02 | 59.50 | 3.35 | 0.06 | 17.87 | 0.05 | 21.00 |
| 2 | 1950 | 2.46 | 0.08 | 12.18 | 0.07 | 14.02 | 3.29 | 0.11 | 9.17 | 0.10 | 10.00 |
| 3 | 1877 | 2.26 | 0.10 | 10.05 | 0.10 | 10.49 | 3.27 | 0.13 | 7.83 | 0.16 | 6.33 |
| 4 | 1560 | 1.38 | 0.22 | 4.49 | 0.27 | 3.76 | 3.19 | 0.25 | 4.04 | 0.22 | 4.50 |
| 5 | 1508.9 | 1.24 | 0.25 | 3.97 | 0.30 | 3.29 | 3.18 | 0.27 | 3.65 | 0.29 | 3.40 |
| 6 | 1492.1 | 1.19 | 0.26 | 3.81 | 0.32 | 3.16 | 3.17 | 0.28 | 3.53 | 0.38 | 2.67 |
| 7 | 1467.6 | 1.12 | 0.28 | 3.60 | 0.34 | 2.98 | 3.17 | 0.30 | 3.36 | 0.47 | 2.14 |
| 8 | 1461.9 | 1.11 | 0.28 | 3.55 | 0.34 | 2.94 | 3.16 | 0.30 | 3.33 | 0.57 | 1.75 |
| 9 | 1455 | 1.09 | 0.29 | 3.50 | 0.35 | 2.90 | 3.16 | 0.30 | 3.28 | 0.69 | 1.44 |
| 10 | 1300 | 0.66 | 0.40 | 2.48 | 0.47 | 2.11 | 3.11 | 0.41 | 2.45 | 0.83 | 1.20 |
| 11 | 1274.6 | 0.59 | 0.43 | 2.35 | 0.50 | 2.01 | 3.11 | 0.43 | 2.34 | 1.00 | 1.00 |
| 12 | 1225.9 | 0.45 | 0.47 | 2.13 | 0.54 | 1.86 | 3.09 | 0.46 | 2.15 | 1.20 | 0.83 |
| 13 | 1140 | 0.22 | 0.55 | 1.81 | 0.61 | 1.64 | 3.06 | 0.54 | 1.87 | 1.44 | 0.69 |
| 14 | 1055 | -0.02 | 0.64 | 1.56 | 0.68 | 1.47 | 3.02 | 0.61 | 1.64 | 1.75 | 0.57 |
| 15 | 950 | -0.31 | 0.74 | 1.34 | 0.76 | 1.32 | 2.98 | 0.70 | 1.42 | 2.14 | 0.47 |
| 16 | 864 | -0.55 | 0.82 | 1.22 | 0.81 | 1.23 | 2.94 | 0.78 | 1.28 | 2.67 | 0.38 |
| 17 | 863.33 | -0.55 | 0.82 | 1.21 | 0.81 | 1.23 | 2.94 | 0.78 | 1.28 | 3.40 | 0.29 |
| 18 | 644.26 | -1.16 | 0.96 | 1.04 | 0.91 | 1.10 | 2.81 | 0.93 | 1.07 | 4.50 | 0.22 |
| 19 | 565.1 | -1.37 | 0.98 | 1.02 | 0.94 | 1.07 | 2.75 | 0.97 | 1.04 | 6.33 | 0.16 |
| 20 | 500 | -1.55 | 0.99 | 1.01 | 0.95 | 1.05 | 2.70 | 0.98 | 1.02 | 10.00 | 0.10 |
Se você não sabe como calcular as probabilidades de excedência dos métodos de Gumbel, Normal e Log-Normal, recomendo ver os artigos de cada um desses métodos aqui no meu site.
Nesse caso, para representar a amostra, usamos a distribuição empírica de Weibull.
Assim, visualizando os resultados da tabela acima, temos:
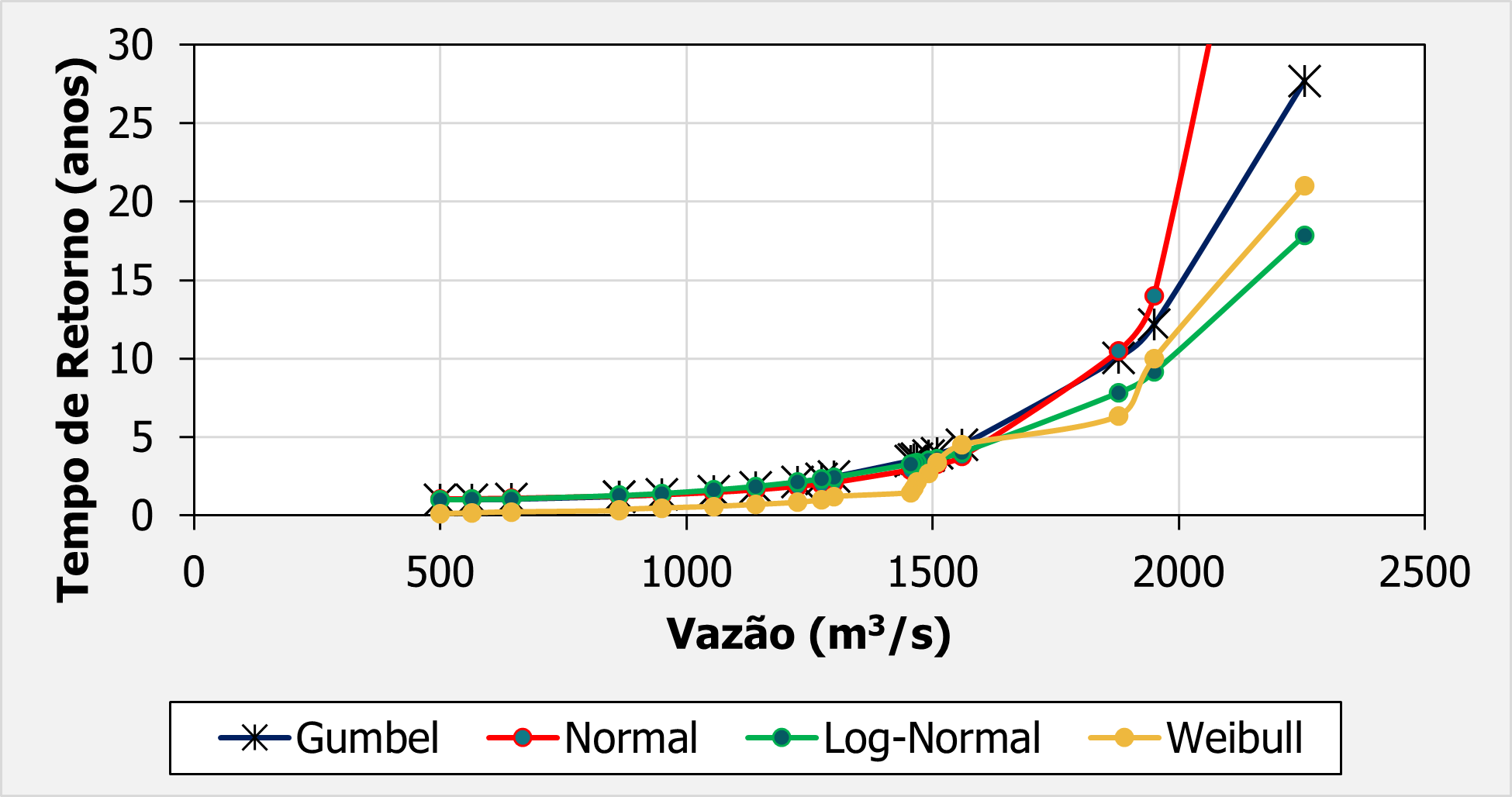
Perceba que, aparentemente, a distribuição log-normal representa melhor os dados observados.
A distribuição normal destoa bastante para os dados observados e a Gumbel está num meio termo, para esse caso.
Isso obviamente não é regra. São só conclusões a partir dos dados observados.
Podemos agora definir uma expressão que calcula o valor da variável aleatória para cada tempo de retorno.
Essas funções são definidas nos artigos anteriores de cada um dos métodos e, serão aqui, resumidas:
(a) Gumbel
$$Q(\mathrm{TR}) = 1270.5 – 463.5(0.45 + 0.7797 \mathrm{ln} \Bigl[\mathrm{ln}\Bigr(\frac{\mathrm{TR}}{\mathrm{TR}-1} \Bigl) \Bigr])$$
(b) Normal
$$Q(\mathrm{TR}) = 1270.5 + 463.5 \frac{1}{\mathrm{TR}}$$
(c) Log-Normal
$$Q(\mathrm{TR}) = 10^{3.073 + 0.176 \frac{1}{\mathrm{TR}}}$$.
Assim, podemos plotar as equações anteriores para diversos valores de TR, resultando em:
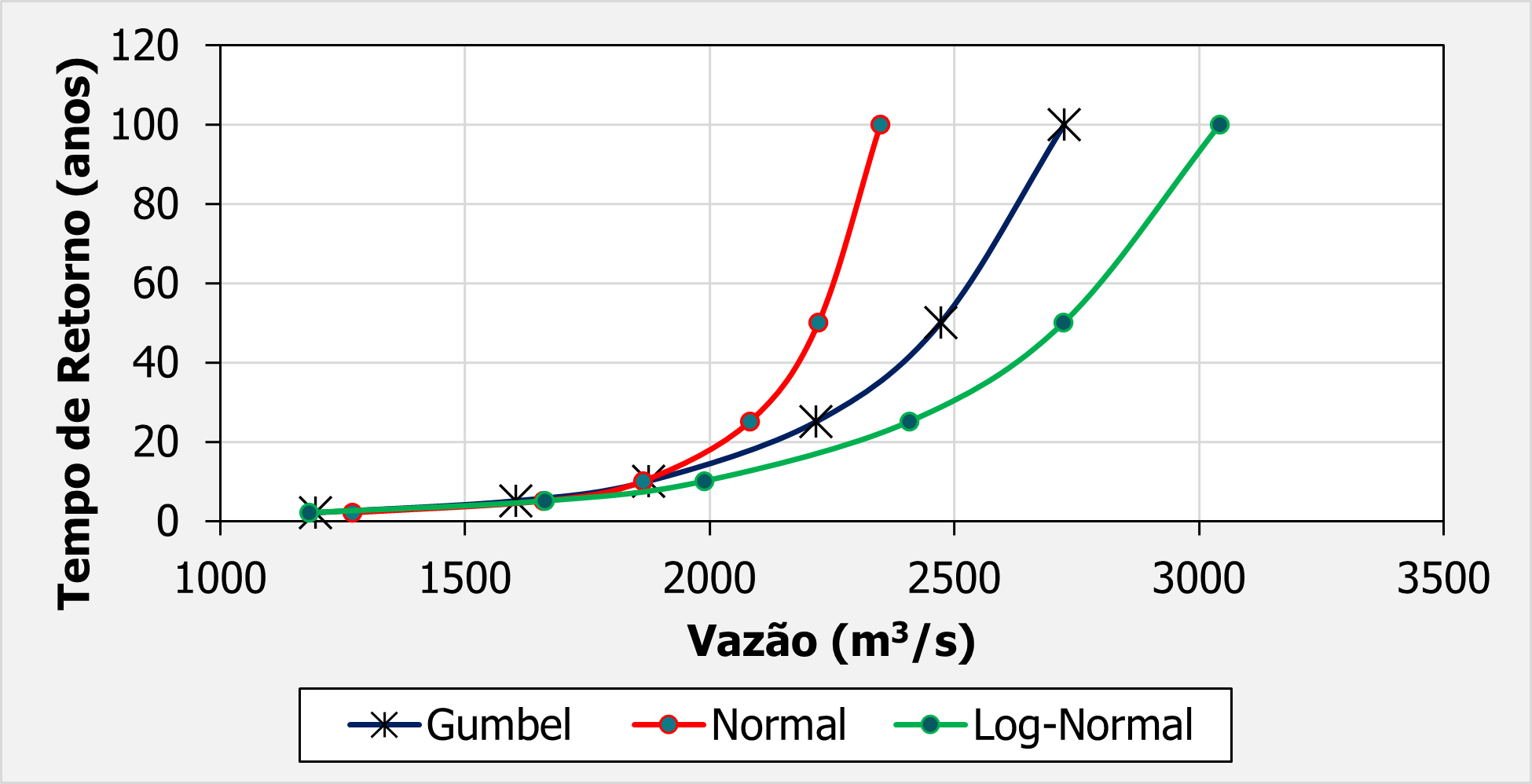
Percebe-se que, nesse caso, a distribuição normal foi contra a segurança, sugerindo valores de TR altos para vazões baixas.
Já a log-normal, apesar de sugerir TRs mais altos, tem mais concordância visual com os dados observados.
Percebe-se pelo gráfico que, para TR = 25 anos, a vazão por Gumbel é 6.5% superior que a vazão pela dist. Normal.
Já a vazão pela log-normal é 15.7% superior à vazão pela dist. Normal.
Exemplo – Ajuste de Cotas Máximas
Para os dados de exemplo anterior, assuma que uma curva chave do tipo:
$$ Q(h) = k_1 h^{k_2}$$
onde $h$ é a cota ou altura d’água tomada de um nível de referência, $k_1$ e $k_2$ são ajustados baseado nas observações de cota ou altura d’água.
Podemos dizer que, se conhecemos a distribuição de $Q$, pela relação anterior, conhecemos a distribuição de $C$ ou de $h$. Assim, determine a curva TR-Cota assumindo que $k_1$ e $k_2$ são iguais a 80 e 1.5.
Qual a discrepância de uma cota para TR = 25 anos?
Assuma que a cota mínima do rio é 300 m, isto é, $z = 300$.
Solução:
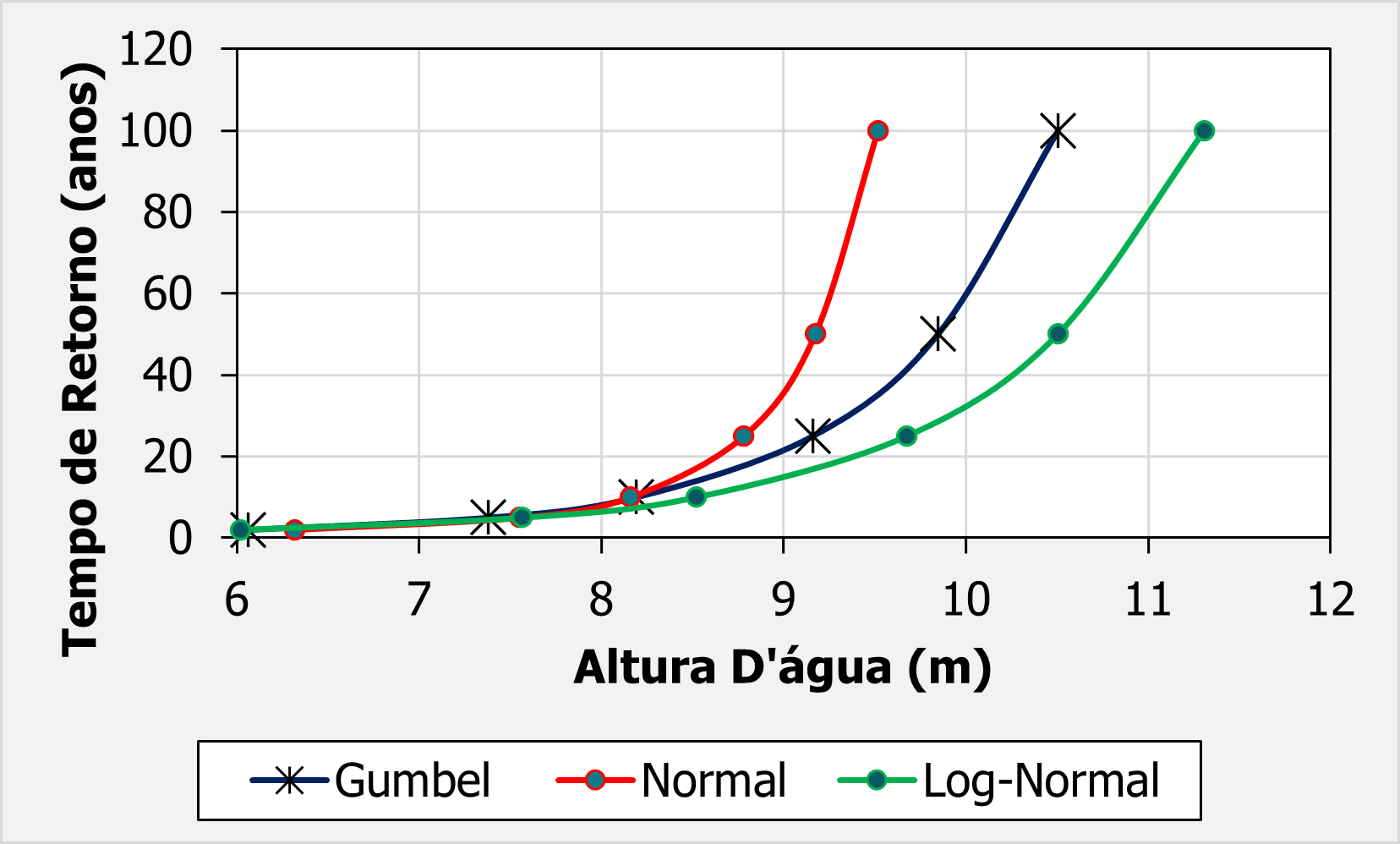
Nesse caso, as discrepâncias aumentam muito a medida que o tempo de retorno aumenta.
Por exemplo, uma diferença de quase 2 m é possível.
Conclusões
É fácil ver com os exemplos apresentados nesse texto que os ajustes variam muito quando tempos de retorno altos são modelados.
Isso implica que, para se ter boas estimativas para tempos de retorno maiores, é necessária uma maior caracterização da amostra.
Geralmente séries de pelo menos 30 anos são usadas.
Nos exemplos aqui, limitamos a 20 anos por questão de organização e espaço.
Porém, tenha em mente que há rios com mais de 100 anos de observações.
Com esse texto, espero que tenha tido um bom entendimento de como funciona o ajuste de vazões máximas em canais ou rios.
