Balanço de Energia (2): Radiação Extraterrestre, Atenuação Atmosférica e Partição em λE, H e G

Este artigo avança no balanço de energia: calcula a radiação extraterrestre diária, trata a atenuação na atmosfera (céu claro e nublado) e fecha a conta em radiação líquida para ligar com evaporação (λE), calor sensível (H) e calor no solo (G). 

1) Conceito, contextualização e importância

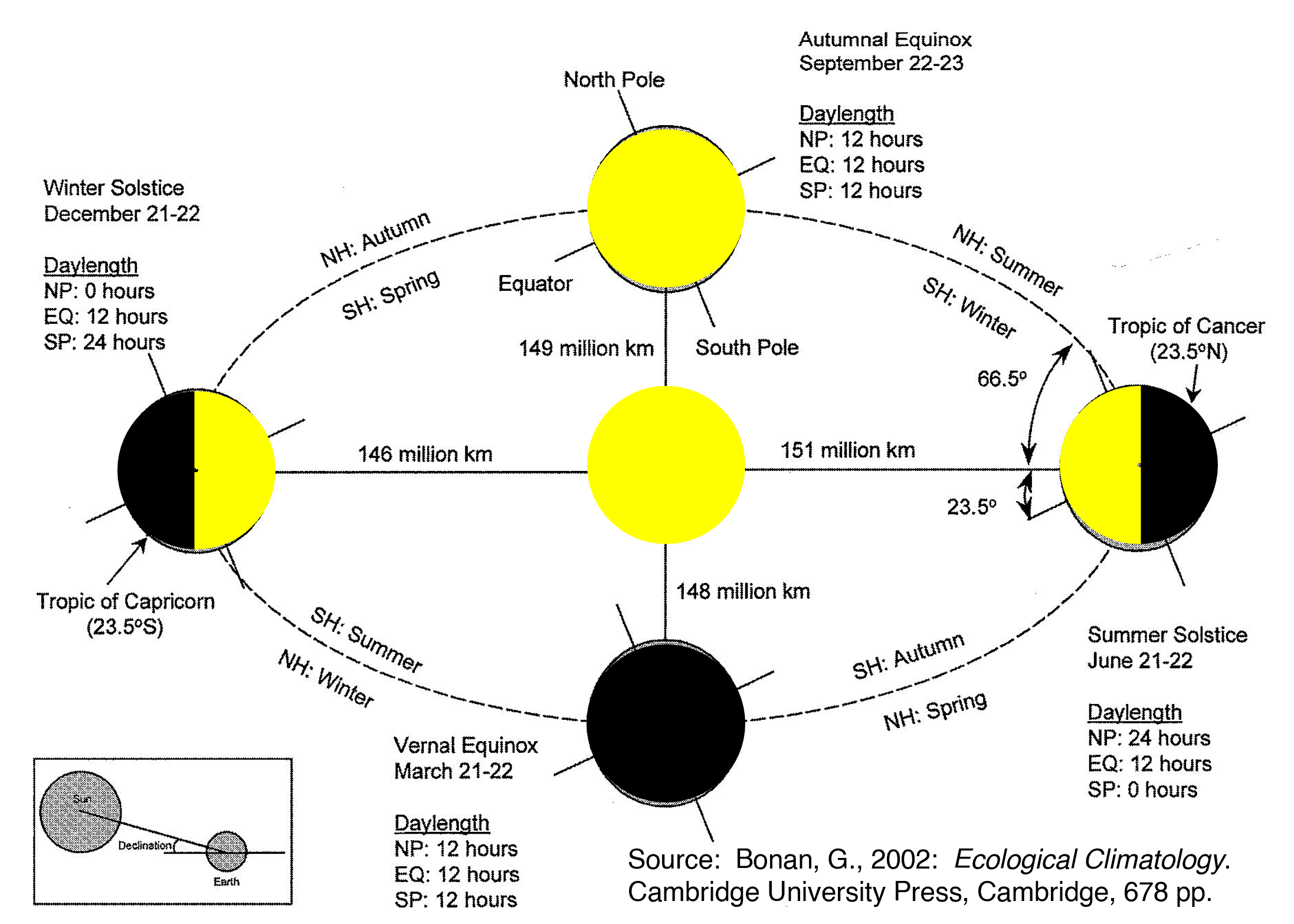
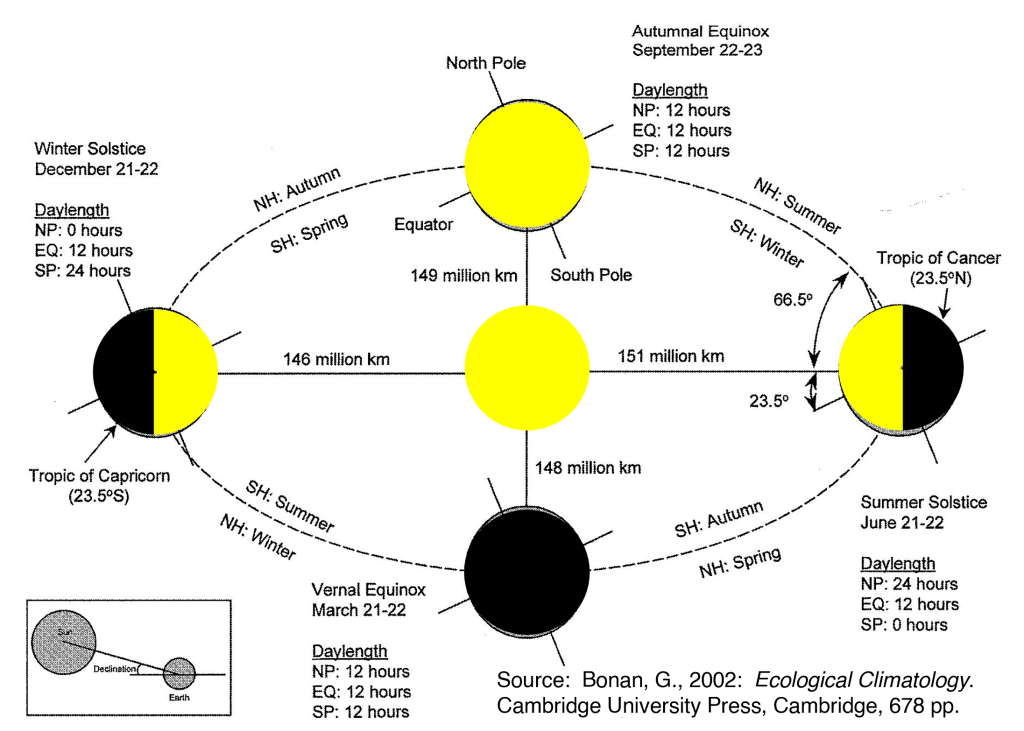
A energia solar que chega ao topo da atmosfera varia ao longo do ano e da latitude. Na superfície, nuvens, gases e aerossóis mudam o que sobra. Esse “saldo” de energia dirige o vapor d’água: mais energia líquida, maior potencial de evaporação.

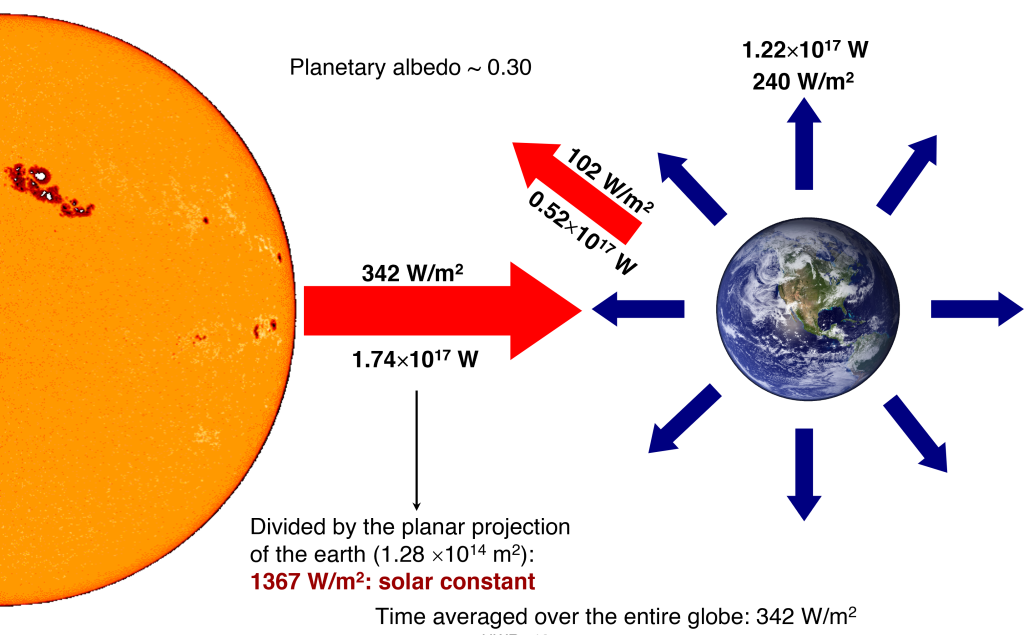
2) Constante solar e radiação no topo da atmosfera

Constante solar: fluxo médio no topo da atmosfera, com raio orbital médio.

$$
R_{so} \approx 1367\ \mathrm{W\,m^{-2}}
$$

• Unidade: W m^-2 (J s^-1 m^-2).
• Varia pouco (manchas solares: flutuações de poucas × 0,1%).

3) Geometria solar diária (dia J e latitude φ)

Usaremos as fórmulas padrão  para um dia juliano J e latitude $\phi$ (em radianos).

3.1. Distância relativa Terra–Sol

$$
d_r = 1 + 0{,}033 \cos\!\left(\frac{2\pi J}{365}\right)
$$

• $d_r$ — fator adimensional (≈1).

3.2. Declinação solar

$$
\delta = 0{,}409 \,\sin\!\left(\frac{2\pi J}{365} – 1{,}39\right)
$$

• $\delta$ — declinação [rad]; captura o efeito da inclinação de 23,5° do eixo da Terra.

3.3. Ângulo horário e pôr do sol

$$
\omega_s = \arccos\!\left(-\tan\phi\,\tan\delta\right),
\qquad
N = \frac{24}{\pi}\,\omega_s
$$

• $\omega_s$ — ângulo horário no pôr do sol [rad].
• $N$ — duração do dia [h].

4) Radiação extraterrestre diária sobre a horizontal

Integrando do nascer ao pôr do sol, obtemos a energia diária por área no topo da atmosfera:

$$
S_{d0}
= \frac{24\cdot60}{\pi}\,G_{sc}\, d_r\,
\Bigl[
\omega_s \sin\phi \sin\delta + \cos\phi \cos\delta \sin\omega_s
\Bigr]
\quad\left[\mathrm{J\,m^{-2}\,dia^{-1}}\right]
$$

• $G_{sc}=1367\ \mathrm{W\,m^{-2}}$ — constante solar.

Às vezes expressamos em “mm eq. de água/dia” dividindo pelo calor latente:

$$
S_{d0}^{(\mathrm{mm/dia})} =
\frac{S_{d0}}{\lambda}
\quad\text{com}\quad
\lambda \approx 2{,}454\times10^{6}\ \mathrm{J\,kg^{-1}}
$$

• $\lambda$ — calor latente de vaporização [J kg^-1]; usando $\rho=1000\ \mathrm{kg\,m^{-3}}$, 1 mm ≡ 1 kg m^-2.

5) Atenuação atmosférica (céu claro e nublado)

5.1. Radiação de onda curta à superfície (empírico de Angström–Prescott)

$$
R_s = \Bigl(a_s + b_s\,\frac{n}{N}\Bigr)\,S_{d0}
$$

• $R_s$ — radiação solar diária na superfície [J m^-2 dia^-1 ou MJ m^-2 dia^-1].
• $n$ — horas de brilho solar medido [h]; $N$ — duração do dia [h].
• $a_s \approx 0{,}25$, $b_s \approx 0{,}50$ (ajuste local).

5.2. Onda longa descendente (céu claro e nublado)

Céu claro (forma de Brutsaert)

$$
\varepsilon_{a,\mathrm{clr}} = 1{,}24 \left(\frac{e_a}{T_a}\right)^{1/7},
\qquad
R_{ld,\mathrm{clr}} = \varepsilon_{a,\mathrm{clr}}\,\sigma\,T_a^{4}
$$

• $e_a$ — pressão de vapor do ar [hPa].
• $T_a$ — temperatura do ar perto da superfície [K].
• $\sigma=5{,}67\times10^{-8}\ \mathrm{W\,m^{-2}\,K^{-4}}$ — constante de Stefan–Boltzmann.

Céu nublado:

$$
R_{ld} \;=\; R_{ld,\mathrm{clr}}\;\Bigl(1 + 0{,}22\, m_c^{2}\Bigr)
$$

• $m_c$ — fração de nebulosidade [0–1].

6) Radiação líquida e partição em λE, H e G

Saldo na interface superfície–atmosfera:

$$
R_n = R_s(1-\alpha_s) + \varepsilon_s\,R_{ld} – R_{lu}
\qquad\text{com}\qquad
R_{lu}=\varepsilon_s\,\sigma\,T_s^{4}
$$

• $R_n$ — radiação líquida [W m^-2].
• $\alpha_s$ — albedo da superfície [–].
• $\varepsilon_s$ — emissividade da superfície [–].
• $T_s$ — temperatura de superfície [K].

Partição (forma comum no dia a dia):

$$
R_n \;\approx\; \lambda E \;+\; H \;+\; G
$$

• $\lambda E$ — fluxo de calor latente (evaporação) [W m^-2].
• $H$ — fluxo de calor sensível [W m^-2].
• $G$ — fluxo de calor no solo (ou água) [W m^-2].

7) Exemplo prático — do topo da atmosfera à superfície

Objetivo: estimar $R_n$ e a fração que pode virar evaporação ($\lambda E$) para um dia claro.

Dados: latitude $\phi=-23{,}5^\circ$ (radianos: $-0{,}410$); dia J=172 (solstício de junho); $a_s=0{,}25$, $b_s=0{,}50$; horas de brilho $n=9{,}0$ h; $T_a=298$ K; $e_a=20$ hPa; fração de nuvens $m_c=0$ (céu claro); albedo $\alpha_s=0{,}15$; emissividade da superfície $\varepsilon_s=0{,}97$; temperatura da superfície $T_s=300$ K.

Passo 1 — geometria e $S_{d0}$: calcular $d_r$, $\delta$, $\omega_s$, $N$ e $S_{d0}$.

$$
\begin{aligned}
d_r &= 1 + 0{,}033\cos\!\Bigl(\tfrac{2\pi\cdot 172}{365}\Bigr) \\
\delta &= 0{,}409\sin\!\Bigl(\tfrac{2\pi\cdot 172}{365} – 1{,}39\Bigr) \\
\omega_s &= \arccos\!\bigl(-\tan(-0{,}410)\tan\delta\bigr),\quad N=\frac{24}{\pi}\omega_s \\
S_{d0} &= \frac{24\cdot60}{\pi}\,G_{sc}\, d_r\,[\,\omega_s \sin\phi \sin\delta + \cos\phi \cos\delta \sin\omega_s\,]
\end{aligned}
$$

Passo 2 — onda-curta à superfície (Angström–Prescott):

$$
R_s = \Bigl(0{,}25 + 0{,}50\,\frac{n}{N}\Bigr)\,S_{d0}
$$

Passo 3 — onda longa descendente (céu claro):

$$
\varepsilon_{a,\mathrm{clr}} = 1{,}24 \left(\frac{e_a}{T_a}\right)^{1/7},
\qquad
R_{ld} = \varepsilon_{a,\mathrm{clr}}\sigma T_a^{4}
$$

Passo 4 — onda longa ascendente da superfície:

$$
R_{lu} = \varepsilon_s\,\sigma\,T_s^{4}
$$

Passo 5 — radiação líquida e partição:

$$
R_n = R_s(1-\alpha_s) + \varepsilon_s\,R_{ld} – R_{lu},
\qquad
R_n \approx \lambda E + H + G
$$

G pode ser assumido como nulo em escalas diárias (saídas e entradas balanceadas entre dia e noite) ou calculado em função do gradiente de temperatura entre o solo e a superfície.

8) Incertezas: o que mais afeta o resultado

• Dados meteorológicos: $n$, $e_a$ e $T_a$ mal medidos propagam erro para $R_s$ e $R_{ld}$.
• Parâmetros de superfície: $\alpha_s$ e $\varepsilon_s$ variam com umidade, cobertura e ângulo solar.
• Empirismos: coeficientes $a_s$, $b_s$ e a forma de correção por nuvens devem ser calibrados localmente.
• Escala temporal/espacial: $R_n$ instantâneo x diário; heterogeneidade dentro do pixel/área.

9) Conclusões e observações

A sequência “atmosfera → superfície → partição” fecha o balanço de energia. Com $R_n$ estimado, quantificamos o potencial de $\lambda E$ (vapor d’água) e de $H$ e $G$.

No próximo passo, conectamos esse balanço com métodos de estimativa de evapotranspiração (Penman–Monteith, Priestley–Taylor) usando $R_n$ como entrada.